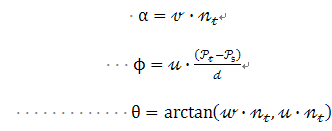7.features特征

3d特征点概述1

3d特征点概述2

各特征描述详见以上大佬博客。

3D点云特征描述与提取是点云信息处理中最基础也是最关键的一部分，点云的识别，分割，重采样，配准，曲面重建等处理大部分算法，都严重依赖特征描述与提取的结果。从尺度上来分，一般分为

• 局部特征的描述

• • 局部的法线等几何形状特征的描述

• 全局特征的描述

• • 全局的拓朴特征的描述

原理：

        在原始表示形式下，点的定义是用笛卡尔坐标系坐标 x, y, z 相对于一个给定的原点来简单表示的三维映射系统的概念，假定坐标系的原点不随着时间而改变，这里有两个点p1和p2分别在时间t1和t2捕获，有着相同的坐标，对这两个点作比较其实是属于不适定问题（ill—posed problem）,因为虽然相对于一些距离测度它们是相等的，但是它们取样于完全不同的表面，因此当把它们和临近的其他环境中点放在一起时，它们表达着完全不同的信息，这是因为在t1和t2之间局部环境有可能发生改变。一些获取设备也许能够提供取样点的额外数据，例如强度或表面反射率等，甚至颜色，然而那并不能完全解决问题，单从两个点之间来   对比仍然是不适定问题。

由于各种不同需求需要进行对比以便能够区分曲面空间的分布情况，应用软件要求更好的特征度量方式，因此作为一个单一实体的三维点概念和笛卡尔坐标系被淘汰了，出现了一个新的概念取而代之：局部描述子（locl descriptor）。
文献中对这一概念的描述有许多种不同的命名，如：形状描述子（shape descriptors）或几何特征（geometric features）,文本中剩余部分都统称为点特征表示。通过包括周围的领域，特征描述子能够表征采样表面的几何性质，它有助于解决不适定的对比问题，理想情况下相同或相似表面上的点的特征值将非常相似（相对特定度量准则），而不同表面上的点的特征描述子将有明显差异。下面几个条件，通过能否获得相同的局部表面特征值，可以判定点特征表示方式的优劣：
（1）刚体变换-----即三维旋转和三维平移变化 不会影响特征向量F估计，即特征向量具有平移旋转不变性。
（2）改变采样密度-----原则上，一个局部表面小块的采样密度无论是大还是小，都应该有相同的特征向量值，即特征向量具有抗密度干扰性。
（3）噪声---数据中有轻微噪声的情况下，点特征表示在它的特征向量中必须保持相同或者极其相似的值，即特征向量对点云噪声具有稳定性。
通常，PCL中特征向量利用快速kd-tree查询 ，使用近似法来计算查询点的最近邻元素，通常有两种查询类型：K邻域查询，半径搜索两种方法

1.法向量估计与快速点特征直方图(FPFH)描述子

法向量估计：

//打开点云代码
pcl::PointCloud::Ptr cloud (new pcl::PointCloud);
pcl::io::loadPCDFile ("../table_scene_lms400.pcd", *cloud);

//创建法线估计估计向量
pcl::NormalEstimation ne;
ne.setInputCloud(cloud);
//创建一个空的KdTree对象，并把它传递给法线估计向量
//基于给出的输入数据集，KdTree将被建立
pcl::search::KdTree::Ptr tree (new pcl::search::KdTree ());
ne.setSearchMethod(tree);
//存储输出数据
pcl::PointCloud::Ptr cloud_normals (new pcl::PointCloud);
//使用半径在查询点周围3厘米范围内的所有临近元素
ne.setRadiusSearch(0.03);
//计算特征值
ne.compute(*cloud_normals);

 法向量估计后计算fpfh：

#pragma once
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

using PointT = pcl::PointCloud;
using PointN = pcl::PointCloud;
using Normal = pcl::PointCloud;

void test_demo()
{
	pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
	pcl::PointCloud::Ptr voxeled_cloud(new pcl::PointCloud);
	pcl::io::loadPCDFile("rabbit.pcd", *cloud);
	//下采样
	pcl::VoxelGrid voxel;
	voxel.setInputCloud(cloud);
	voxel.setLeafSize(0.1f, 0.1f,0.1f);
	
	voxel.filter(*voxeled_cloud);

	//法向量
	pcl::NormalEstimationOMPne;
	ne.setNumberOfThreads(4);
	ne.setInputCloud(voxeled_cloud);
	pcl::search::KdTree::Ptr tree;
	ne.setSearchMethod(tree);
	ne.setRadiusSearch(0.5f);
	PointN::Ptr normal_cloud(new PointN);
	ne.compute(*normal_cloud);

	//显示法向量
	for (int i = 0; i < normal_cloud->size(); ++i)
	{
		normal_cloud->points[i].x = voxeled_cloud->points[i].x;
		normal_cloud->points[i].y = voxeled_cloud->points[i].y;
		normal_cloud->points[i].z = voxeled_cloud->points[i].z;


	}
	pcl::visualization::PCLVisualizer viewer;
	viewer.setBackgroundColor(0, 0, 0);
	
	viewer.addPointCloud(voxeled_cloud,"voxel_cloud");
	int level = 1; // 多少条法向量集合显示成一条
	float scale = 0.05; // 法向量长度
	viewer.addPointCloudNormals(normal_cloud, level, scale, "normals");
	//显示原点云
	viewer.addPointCloud(cloud, "cloud");

	pcl::visualization::PointCloudColorHandlerCustom color_handler(normal_cloud, 255, 0, 0);
	//fpfh特征直方图
	pcl::FPFHEstimationfpfh;
	fpfh.setInputCloud(voxeled_cloud);
	//fpfh.setSearchSurface(cloud);
	fpfh.setInputNormals(normal_cloud);
	pcl::search::KdTree::Ptr tree1(new pcl::search::KdTree);
	fpfh.setSearchMethod(tree1);
	pcl::PointCloud::Ptr fpfh_cloud(new(pcl::PointCloud));
	fpfh.setRadiusSearch(0.05f);
	//检查法向量
	for (int i = 0; i < normal_cloud->size(); i++)
	{
		if (!pcl::isFinite((*normal_cloud)[i]))
		{
			PCL_WARN("normals[%d] is not finite\n", i);
		}
	}
	fpfh.compute(*fpfh_cloud);

	viewer.spin();
	system("pause");


}

2.点特征直方图（PFH）描述子

正如点特征表示法所示，表面法线和曲率估计是某个点周围的几何特征基本表示法。虽然计算非常快速容易，但是无法获得太多信息，因为它们只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。

然而大部分场景中包含许多特征点，这些特征点有相同的或者非常相近的特征值，因此采用点特征表示法，其直接结果就减少了全局的特征信息。

那么三维特征描述子中一位成员：点特征直方图(Point Feature Histograms)，我们简称为PFH，从PCL实现的角度讨论其实施细节。PFH特征不仅与坐标轴三维数据有关，同时还与表面法线有关。

PFH计算方式通过参数化查询点与邻域点之间的空间差异，并形成一个多维直方图对点的k邻域几何属性进行描述。直方图所在的高维超空间为特征表示提供了一个可度量的信息空间，对点云对应曲面的6维姿态来说它具有不变性，并且在不同的采样密度或邻域的噪音等级下具有鲁棒性。

点特征直方图（PFH）表示法是基于点与其k邻域之间的关系以及它们的估计法线，简言之，它考虑估计法线方向之间所有的相互作用，试图捕获最好的样本表面变化情况，以描述样本的几何特征。因此，合成特征超空间取决于每个点的表面法线估计的质量。

如图所示，表示的是一个查询点(Pq) 的PFH计算的影响区域，Pq 用红色标注并放在圆球的中间位置，半径为r， (Pq)的所有k邻元素（即与点Pq的距离小于半径r的所有点）全部互相连接在一个网络中。最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图，因此存在一个O(k) 的计算复杂性。

      

为了计算两点Pi和Pj及与它们对应的法线Ni和Nj之间的相对偏差，在其中的一个点上定义一个固定的局部坐标系，如图2所示。

               

使用上图中uvw坐标系，法线 和 之间的偏差可以用一组角度来表示，如下所示：

  估计PFH特征

点特征直方图（PFH）在PCL中的实现是pcl_features模块的一部分。默认PFH的实现使用5个区间分类（例如：四个特征值中的每个都使用5个区间来统计），

以下代码段将对输入数据集中的所有点估计其对应的PFH特征。

computePointPFHSignature (const pcl::PointCloud &cloud,
                          const pcl::PointCloud &normals,
                          const std::vector &indices,
                          int nr_split,
                          Eigen::VectorXf &pfh_histogram);

3.SHOT

主要代码

typedef pcl::PointXYZ PointT;
typedef pcl::Normal PointNT;
typedef pcl::SHOT352 FeatureT;
pcl::SHOTEstimation shot;
	shot.setRadiusSearch(18 * resolution);
	shot.setInputCloud(keys);
	shot.setSearchSurface(cloud);
	shot.setInputNormals(cloud_normal);
	//shot.setInputReferenceFrames(lrf);  //也可以自己传入局部坐标系
	pcl::PointCloud::Ptr features(new pcl::PointCloud);
	shot.compute(*features);

4.ROPS

由于RoPS是基于网格数据，所以如果输入的是点云数据需要先进行网格化处理。

主要代码

pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
	pcl::io::loadPCDFile(argv[1], *cloud);
	
	// 加载关键点
	pcl::PointCloud::Ptr key_points(new pcl::PointCloud);
	pcl::io::loadPCDFile(argv[2], *key_points);
	// 计算法向量
	pcl::NormalEstimation n;
	pcl::PointCloud::Ptr normals(new pcl::PointCloud);
	pcl::search::KdTree::Ptr tree(new pcl::search::KdTree);
	tree->setInputCloud(cloud);
	n.setInputCloud(cloud);
	n.setSearchMethod(tree);
	n.setKSearch(20);
	n.compute(*normals);
	// 连接数据
	pcl::PointCloud::Ptr cloud_with_normals(new pcl::PointCloud);
	pcl::concatenateFields(*cloud, *normals, *cloud_with_normals);
	//* cloud_with_normals = cloud + normals
	// ---- rops基于网格，所以要先将pcd点云数据重建网格 ---
	// Create search tree*
	pcl::search::KdTree::Ptr tree2(new pcl::search::KdTree);
	tree2->setInputCloud(cloud_with_normals);
	
	pcl::GreedyProjectionTriangulation gp3;// Initialize objects
	pcl::PolygonMesh triangles;
	// Set the maximum distance between connected points (maximum edge length)
	gp3.setSearchRadius(0.025);
	gp3.setMu(2.5); // Set typical values for the parameters
	gp3.setMaximumNearestNeighbors(100);
	gp3.setMaximumSurfaceAngle(M_PI / 4); // 45 degrees
	gp3.setMinimumAngle(M_PI / 18); // 10 degrees
	gp3.setMaximumAngle(2 * M_PI / 3); // 120 degrees
	gp3.setNormalConsistency(false);
	gp3.setInputCloud(cloud_with_normals);
	gp3.setSearchMethod(tree2);
	gp3.reconstruct(triangles);	// Get result
	
	// ----- rops 描述-------
	// 由于pcl_1.8.0中rops还没有定义好的结构，所以采用pcl::Histogram存储描述子
	pcl::ROPSEstimation> rops;
	rops.setInputCloud(key_points);
	rops.setSearchSurface(cloud);
	rops.setNumberOfPartitionBins(5);
	rops.setNumberOfRotations(3);
	rops.setRadiusSearch(0.01);
	rops.setSupportRadius(0.01);
	rops.setTriangles(triangles.polygons);
	rops.setSearchMethod(pcl::search::KdTree::Ptr(new pcl::search::KdTree < pcl::PointXYZ>));
	//feature size = number_of_rotations * number_of_axis_to_rotate_around * number_of_projections * number_of_central_moments
	//unsigned int feature_size = number_of_rotations_ * 3 * 3 * 5; //计算出135
	pcl::PointCloud> description;
	rops.compute(description);  // 结果计算的是描述子。。需传入inputcloud和surface
	std::cout << "size is " << description.points.size()<::Ptr cloud(new pcl::PointCloud);
	pcl::io::loadPCDFile(argv[1], *cloud);
	
	// 加载关键点
	pcl::PointCloud::Ptr key_points(new pcl::PointCloud);
	pcl::io::loadPCDFile(argv[2], *key_points);
	// 计算法向量
	pcl::NormalEstimation n;
	pcl::PointCloud::Ptr normals(new pcl::PointCloud);
	pcl::search::KdTree::Ptr tree(new pcl::search::KdTree);
	tree->setInputCloud(cloud);
	n.setInputCloud(cloud);
	n.setSearchMethod(tree);
	n.setKSearch(20);
	n.compute(*normals);
	// 连接数据
	pcl::PointCloud::Ptr cloud_with_normals(new pcl::PointCloud);
	pcl::concatenateFields(*cloud, *normals, *cloud_with_normals);
	//* cloud_with_normals = cloud + normals
	// ---- rops基于网格，所以要先将pcd点云数据重建网格 ---
	// Create search tree*
	pcl::search::KdTree::Ptr tree2(new pcl::search::KdTree);
	tree2->setInputCloud(cloud_with_normals);
	
	pcl::GreedyProjectionTriangulation gp3;// Initialize objects
	pcl::PolygonMesh triangles;
	// Set the maximum distance between connected points (maximum edge length)
	gp3.setSearchRadius(0.025);
	gp3.setMu(2.5); // Set typical values for the parameters
	gp3.setMaximumNearestNeighbors(100);
	gp3.setMaximumSurfaceAngle(M_PI / 4); // 45 degrees
	gp3.setMinimumAngle(M_PI / 18); // 10 degrees
	gp3.setMaximumAngle(2 * M_PI / 3); // 120 degrees
	gp3.setNormalConsistency(false);
	gp3.setInputCloud(cloud_with_normals);
	gp3.setSearchMethod(tree2);
	gp3.reconstruct(triangles);	// Get result
	
	// ----- rops 描述-------
	// 由于pcl_1.8.0中rops还没有定义好的结构，所以采用pcl::Histogram存储描述子
	pcl::ROPSEstimation> rops;
	rops.setInputCloud(key_points);
	rops.setSearchSurface(cloud);
	rops.setNumberOfPartitionBins(5);
	rops.setNumberOfRotations(3);
	rops.setRadiusSearch(0.01);
	rops.setSupportRadius(0.01);
	rops.setTriangles(triangles.polygons);
	rops.setSearchMethod(pcl::search::KdTree::Ptr(new pcl::search::KdTree < pcl::PointXYZ>));
	//feature size = number_of_rotations * number_of_axis_to_rotate_around * number_of_projections * number_of_central_moments
	//unsigned int feature_size = number_of_rotations_ * 3 * 3 * 5; //计算出135
	pcl::PointCloud> description;
	rops.compute(description);  // 结果计算的是描述子。。需传入inputcloud和surface
	std::cout << "size is " << description.points.size()<