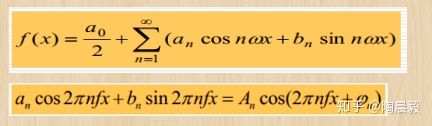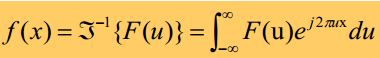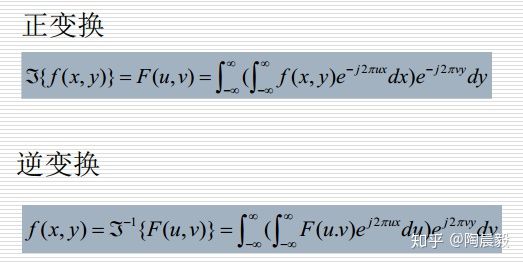matlab求傅里叶级数展开式_明明学过积分和三角函数就能秒理解傅里叶变换.........
<前言>
傅里叶分析之掐死教程，我看了，说实话我觉得有点绕，如果没学过傅里叶变换我觉得不可能看一遍就懂，估计会卡死很久。尤其是那些矢量图和大海螺旋图，让我一脸懵逼，怀疑自己没学过傅里叶变换。
Heinrich：傅里叶分析之掐死教程（完整版）更新于2014.06.06zhuanlan.zhihu.com
仔细一想，作者说“要让读者在不看任何数学公式的情况下理解傅里叶分析”。这就麻烦了，数学语言简洁直接，要最快理解显然应该不应该走这条路，而应该先把相关的数学知识搞清楚到能理解傅里叶变换的程度。
当然像作者这样去讲述也是很棒的（尤其是我引用的那张图，很清晰），但是我总觉得这样会使已经有一点数学基础的人看的更晕，没有数学基础的同学也不可能很快理解。
<正文>
我们可以将任意信号强度随时间变化的规律写成函数f(x)，x表示时间。
任意信号往往非常复杂毫无规律，难以用数学式表示，于是我们希望将函数f(x)分解为几个简单的函数相加的形式，分解如下表示：
我们自然希望找到一种分解（选择一种合适的基底函数），能够很方便地求出系数c_n。数学家告诉我们三角函数、复指数函数正是合适的基底函数。
利用三角函数系或复指数函数系展开的函数级数被称为傅立叶级数。
周期为T的函数f(x)傅里叶级数展开如下：
数学家（知道我们不会算）同时告诉了我们系数：
把频率作为x轴（数值用n表示），把振幅An作为y轴，可以画出频谱图（幅度谱）：
利用频谱图还可以直观地分析各谐波分量的组成以及比重。当然还有相位谱图，频率作为x轴（数值用n表示），相位φ作为y轴就好了。
如上所述，我们可以将一个复杂的周期性信号分解成几个简单的简谐波叠加。
（把复杂的波形变成如上几根线段，真是太爽了！）
那非周期性函数怎么办？非周期函数的傅立叶展开式，周期无限大，采用傅立叶积分。
傅立叶积分是傅立叶级数取极限得到的，推导过程如下图所示：
（前方复指数函数警告，没学过可以跳过下图推导）
对比一下傅里叶级数的式子：
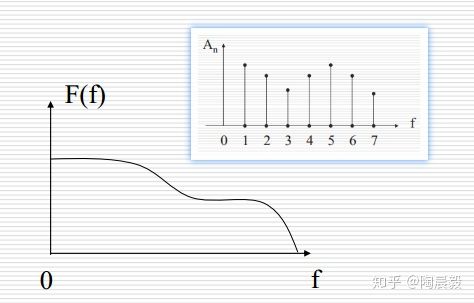
非周期信号的F(f)就是周期性信号的An（也就是一开始说的系数）。
非周期信号和周期性信号的区别就在于频谱是否连续：
<总结一下>
所以呢，傅里叶变换就是在分解一个函数的过程中，某个叫傅里叶的人发现某种分解方式特别简洁好算，然后就把这种分解方式（变换）命名为傅里叶变换。
从数学上理解，就是把一个函数写成几个（或者无限个，取个极限）函数（三角函数或复指数函数）相加的过程。
从信号处理的角度来理解，就是把一个在时域上非常复杂的信号函数（随时间变化非常复杂），转变为在频域上相对简单便于处理的频谱函数的过程。
下图非常直观地表现了这一过程。基底函数是三角函数，原始信号函数前面那个是图像类似于矩形波的函数。如果要分解真正的矩形波（显然是非周期函数），频谱图像就是连续的。
很多时候会把f写成u：
还有傅里叶反（逆）变换：
傅立叶变换是互逆的，唯一的。如果没有这一性质，就不能将一个时域的函数变换为频域进行分析，再变换回时域。
值得注意的是，上文我们以信号随时间的变化举例来理解一维的傅里叶变换，或者说应用一维傅里叶变换处理随时间变换的信号问题。但是傅里叶变换在数学上仅仅是一个函数变换，具体变量的含义并无规定。
<遥感数字图像处理原理课的复习>
通过“处理时间信号”的例子，现在我们已经理解了傅里叶变换。很容易将傅里叶变换拓展至多维。二维函数的傅立叶变换和反变换分别定义为：
处理静态二维图像需要使用二维傅里叶变换。
f(x,y)是一幅图像，F(u,v)是它的傅立叶变换。u, v是傅立叶变换的空间频率。
对比一下利用一维傅里叶变换处理时间信号：
- 一维傅里叶变换（处理时间信号）：时域的函数变换为频域，进行分析，再变换回时域。
- 二维傅里叶变换（处理二维图像）：空域的函数变换为频域，进行分析，再变换回空域。
应该不难理解。
空间频率在上一节课《数字图像处理的光学基础》中已经讲过，可以理解为等相位线在x,y坐标投影的截距的倒数。对于图像信号，空间频率是指单位长度内亮度作周期性变化的次数。
空间频率的概念在图像处理中十分重要。了解噪声、线、细节、背景或平滑区域等对应的空间频率特性，才能更好地对图像进行处理。
空间频率知识细节对应到光学，涉及阿贝成像理论：
物体经过光学系统到像经历了两个过程：
（1）物经过光学系统后，在它的后焦面上形成衍射图样（夫琅和费衍射）。
（2）以衍射图样为次波波源，在像平面上产生振幅叠加而构成了物的像。
这两个过程分别对应傅立叶正变换和傅里叶反变换。阿贝在数学上证明了，二次成像过程就是对二维光场的复振幅进行正、反两次傅立叶变换的过程。
第一次是把光场复振幅的空间分布，变成光学系统后焦面上的空间频率的分布。
第二次的作用是把空间频率分布还原成光场复振幅的空间分布。
光的二次傅立叶变换，是数字图像处理中改善图像质量的光学理论基础。