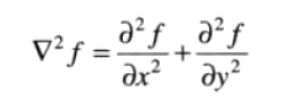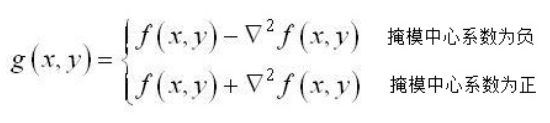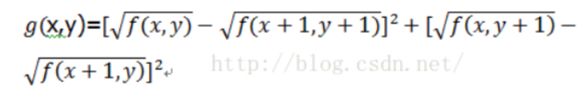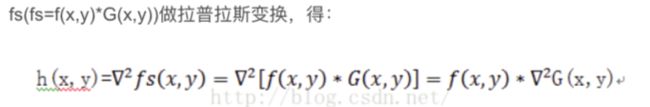头条面经（同学一）

一面：

1. 图像降噪算法

滤波类：比较传统的一类算法，通过设计滤波器对图像进行处理，特点是速度往往比较快，很多卷积滤波可以借助快速傅立叶变化。（重点回答，主要考察滤波类）滤波类包括均值滤波，高斯滤波，统计中值滤波，双边滤波，引导滤波，NLM（Non-Local means）算法，参考我的博客：https://blog.csdn.net/Victory_tc/article/details/97314568

稀疏表达类：自然图像不同于随机噪声/人造的噪声，在于其总会在某一个模型（判别式模型）下存在稀疏表达，而躁声往往不存在这种稀疏表达。

外部先验证（包括深度学习的方法）：如果含有噪声的图片本身没有什么规律，我们可以借助其它类似但是没有噪声的图片总结图片固有的属性。最具有代表的是混合高斯模型，最火的是深度学习的方法（通过大量的数据学习得到一个高度复杂的图片约束器

聚类低秩性：稀疏性和低秩性都是自然图像常见特征，低秩数据直接存在与一个低微子空间，以此约束来区别噪声。

推荐博客：https://zhuanlan.zhihu.com/p/32502816

2.图像增强算法

图像增强主要解决由于图像的灰度级范围较小造成的对比度较低的问题，目的就是将输出图像的灰度级放大到指定的程度，使得图像中的细节看起来增加清晰，目的是提高图像的对比度，是图像更加清晰，丰富图像细节。对比度增强有几种常用的方法，如线性变换、分段线性变换、伽马变换、直方图正规化、直方图均衡化、局部自适应直方图均衡化等。

线性变换，分段线性变换，伽马变换，直方图正规化，直方图均衡化，局部自适应直方图均衡化的原理以及python代码参考我的博客：https://blog.csdn.net/Victory_tc/article/details/97361911

其它图像增强算法：

指数图像增强的表达为：S = cR^r，通过合理的选择c和r可以压缩灰度范围，例如c=1.0/255.0, r=2实现。

对数图像增强是图像增强的一种常见方法，其公式为： S = c log(r+1)，其中c是常数（以下算法c=255/(log(256)），这样可以实现整个画面的亮度增大。

马赛克算法的原理：利用中心像素来表示邻域像素。

曝光过度问题处理：对于曝光过度问题，可以通过计算当前图像的反相（255-image)，然后取当前图像和反相图像的较小者为当前像素位置的值。过度曝光原理：图像翻转，然后求原图与反图的最小值。

基于拉普拉斯算子的图像增强： 利用拉普拉斯算子进行图像增强本质是利用图像的二次微分对图像进行锐化，在图像领域中微分是锐化，积分是模糊，利用二次微分对图像进行锐化即利用邻域像素提高对比度。与一阶微分相比，二阶微分的边缘定位能力更强，锐化效果更好。

拉普拉斯算子（线性算子，（任意阶微分算子都是线性的））:

所以拉普拉斯算子为：

也就是一个点的拉普拉斯的算子计算结果是上下左右的灰度的和减去本身灰度的四倍。可以根据二阶微分的不同定义，所有符号相反，也就是上式所有灰度值全加上负号，就是-1，-1，-1，-1，4。但要注意，符号改变，锐化的时候与原图的加或减应当相对变化。上面是四邻接的拉普拉斯算子，将这个算子旋转45°后与原算子相加，就变成八邻域的算子了，也就是一个像素周围一圈8个像素的和与中间像素8倍的差，作为拉普拉斯计算结果。因为要强调图像中突变（细节），在平滑灰度的区域无响应，所以模板系数和为0，也是二阶微分必备条件。

拉普拉斯算子是最简单的各向同性的微分算子，具有旋转不变性质，特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样，拉普拉斯算子也会增强图像中的噪声，有时用拉普拉斯算子进行边缘检测时，可将图像先进行平滑处理。

图像锐化处理的作用是使灰度反差增强，从而使模糊图像变得更加清晰，图像模糊的实质就是图像受到平均运算或积分运算，因此可以对图像进行逆运算，如微分运算能够突出图像细节，使图像变得更为清晰。由于拉普拉斯是一种微分算子，它的应用可增强图像中灰度突变的区域，减弱灰度的缓慢变化区域；锐化处理可选择拉普拉斯算子对原图像进行处理，产生描述灰度突变的图像，再将拉普拉斯图像与原始图像叠加而产生锐化图像。

这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果，同时又能保留背景信息，将原始图像叠加到拉普拉斯变换的处理结果中去，可以使图像中的各灰度值得到保留，使灰度突变处的对比度得到增强，最终结果是在保留图像背景的前提下，突现出图像中小的细节信息。但其缺点是对图像中的某些边缘产生双重响应。

3. 边缘检测算子：Robert prewit sobel 拉普拉斯 canddy

边缘检测算法（主要用于特征的提取，保留图像的结构属性）是图像处理和计算机视觉的基本问题，主要解决数字图像中亮度明显变化的点，图像属性的显著变化通常反映了属性的重要事件和变化包括深度上的不连续、表面方向不连续、物质属性变化和场景照明变化。边缘检测大多数可以划分为两类：基于查找一类（一阶导数的最大值或者最小值）和基于零穿越的一类（二阶导数的零点）；噪声和边缘都属于高频信号，噪声给边缘检测检测带来了困难，而降噪又会使得边缘模糊；一阶的有Roberts Cross算子，Prewitt算子，Sobel算子，Canny算子，Krisch算子，罗盘算子；而二阶的还有Marr-Hildreth，在梯度方向的二阶导数过零点。

边缘和物体间的边界并不等同，边缘指的是图像中像素的值有突变的地方，而物体间的边界指的是现实场景中的存在于物体之间的边界。有可能有边缘的地方并非边界，也有可能边界的地方并无边缘，因为现实世界中的物体是三维的。

在实际的图像分割中，往往只用到一阶和二阶导数，虽然，原理上，可以用更高阶的导数，但是，因为噪声的影响，在纯粹二阶的导数操作中就会出现对噪声的敏感现象，三阶以上的导数信息往往失去了应用价值

Roberts算子：是一种利用局部差分算子寻找边缘的算子，2*2算子模板 (关联(x,y),(x+1,y), (x, y+1), (x+1, y+1))

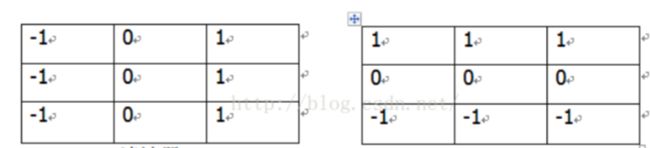
Sobel算子：一阶微分算子，利用一个像素的临近区域来计算像素的梯度，然后根据一定的绝对值进行取舍。

Prewitt算子：与Sobel算子类似，算子模版中的值略有不同。

log 算子：先对图像进行高斯变化（图像的平滑，也就是高斯滤波），后对平滑后的图像进行拉普拉斯变化（laplace 锐化（图像增强））

即先对图象平滑，后拉氏变换求二阶微分，等效于把拉氏变化作用于平滑函数，得到1个兼有平滑和二阶微分作用的模板，再与原来的图像进行卷积。用Marr-Hildreth模板与图像进行卷积的优点在于，模板可以预先算出，实际计算可以只进行卷积。

Log算子的特点：

（1）通过图象平滑，消除了一切尺度小于σ的图像强度变化;

（2）若用其它微分法，需要计算不同方向的微分，而拉普拉斯微分无方向性，因此可以节省计算量;

（3）它定位精度高，边缘连续性好，可以提取对比度较弱的边缘点。

LOG滤波器也有它的缺点:当边缘的宽度小于算子宽度时，由于过零点的斜坡融合将会丢失细节。

LOG滤波器可以近似为两个指数函数之差，即DOG ( Difference Of twoGaussians functions):

Canny 算子：

该算子功能比前面几种都要好，但是它实现起来较为麻烦，Canny算子是一个具有滤波，增强，检测的多阶段的优化算子，在进行处理前，Canny算子先利用高斯平滑滤波器来平滑图像以除去噪声，Canny分割算法采用一阶偏导的有限差分来计算梯度幅值和方向，在处理过程中，Canny算子还将经过一个非极大值抑制的过程，最后Canny算子还采用两个阈值来连接边缘。

Canny边缘检测算法

step1: 用高斯滤波器平滑图象；

step2: 用一阶偏导的有限差分来计算梯度的幅值和方向；

step3: 对梯度幅值进行非极大值抑制

step4: 用双阈值算法检测和连接边缘

Canny 算子详解：https://www.cnblogs.com/cfantaisie/archive/2011/06/05/2073168.html

python 代码实现参考博客：https://www.cnblogs.com/wj-1314/p/9800272.html

5. 手写马赛克（Masaic）代码

马赛克算法的原理：利用中心像素来表示邻域像素（在图片中的某一块区域,打上马赛克,马赛克的算法就是在N个小块儿区域内(比如有很多个10 * 10小块儿),使用一个随机的像素值,代替其他像素值.）

python代码：

import cv2
import numpy as np

img = cv2.imread('image0.jpg', 1)
imgInfo = img.shape
height = imgInfo[0]
width = imgInfo[1]

# 在height 50 - 100 width 100 - 200 上 打码
# 在 10 * 10 的方格内,选取一个像素,进行填充
k = 0
for m in range(100, 200):
    for n in range(100,250):
        if m%10 == 0 and n%10 == 0:
            for i in range(10):
                for j in range(10):
                    (b, g, r) = img[m, n]
                    img[i + m, j + n] = (b, g, r)

cv2.imshow('image', img)
cv2.waitKey(0)

毛玻璃算法：毛玻璃是通过在某一个区域内随机选择一个像素点,用来代替当前像素点的做法,实现一个类似毛玻璃的效果。

python：

import cv2
import numpy as np
import random

img = cv2.imread('image0.jpg', 1)
imgInfo = img.shape
height = imgInfo[0]
width = imgInfo[1]

dst = np.zeros([height, width, 3], np.uint8)

mm = 8
for m in range(height - mm):
    for n in range(width - mm):
        index = int(random.random() * 8)
        (b, g, r) = img[m+index, n+index]
        dst[m, n] = (b, g, r)

cv2.imshow('image', dst)
cv2.waitKey(0)

6. 手写高斯滤波以及优化

参考个人博客：https://blog.csdn.net/Victory_tc/article/details/97314568

7. c++多态：重载和虚函数
8. 虚函数表、虚函数指针大小
9. gcc编译过程
10.手写洗牌算法：N张牌等概率出现在每个位置

二面：

 

1. C++ 11新特性
2. const作用：const int func(const int& A) const 
3. new/malloc区别

相同点：

4. 虚继承
5.四种类型转换
6.智能指针
7.左值右值、move，
8.手写双向链表随机插入新元素的类
9.机器学习：Adam、SGD、RMSProp区别

手写总结
10.1*1卷积的作用

手写总结
11. 贝叶斯估计与最大似然估计的区别

12.c++初始化列表， export关键字

13.C++类的析构函数不用虚函数，对继承有什么影响？

 

三面：

1.手写均值滤波以及优化代码

已总结
2.ML/DL数据处理相关操作

数据预处理相关操作：去除唯一属性、处理缺失值、属性编码、数据标准化正则化、特征选择、主成分分析

去除唯一属性：唯一属性通常是一些id属性，这些属性并不能刻画样本自身的分布规律；删除即可。

处理缺失值：直接使用含有缺失值的特征；删除含有缺失值的特征（该方法在包含缺失值的属性含有大量缺失值而仅仅包含极少量有效值时是有效的）；缺失值补全。

常见的缺失值补全方法：均值插补、同类均值插补、建模预测、高维映射、多重插补、极大似然估计、压缩感知和矩阵补全。

高维映射：将属性映射到高维空间，采用独热码编码（one-hot）技术。将包含K个离散取值范围的属性值扩展为K+1个属性值，若该属性值缺失，则扩展后的第K+1个属性值置为1。

属性编码：

（1）特征二元化

特征二元化的过程是将数值型的属性转换为布尔值的属性，设定一个阈值作为划分属性值为0和1的分隔点。

（2）独热编码（One-HotEncoding）

独热编码采用N位状态寄存器来对N个可能的取值进行编码，每个状态都由独立的寄存器来表示，并且在任意时刻只有其中一位有效。

独热编码的优点：能够处理非数值属性；在一定程度上扩充了特征；编码后的属性是稀疏的，存在大量的零元分量。

数据标准化正则化：数据标准化是将样本的属性缩放到某个指定的范围。

特征选择：从给定的特征集合中选出相关特征子集的过程称为特征选择，进行特征选择的两个主要原因是：减轻维数灾难问题；降低学习任务的难度。常见的特征选择方法分为三类：过滤式（filter）、包裹式（wrapper）、嵌入式

主成分分析：降维度