从全连接神经网络到cnn网络的backpropagation算法解析
写在前面的话
深度学习由于引进了keras,tensorflow,pytorch等库以后,网络的搭建以及后向学习(backpropagation)变得非常易于实现,很多时候我们其实只需要一个backward函数便可以利用已经实现的库函数完成网络的学习过程。这样固然是一个极好的过程,但我相信如果能从数学的角度理解后向学习,将更有利于我们去理解网络,搭建更符合于我们自身需求的网络结构。本篇博客,我希望能够从数学的角度对整个后向学习过程进行推导,希望能帮助到和我有同样需求的人。
一、全连接神经网络
所谓的全连接神经网络就是前一层的所有节点的内容都对下一层的所有节点的输出产生影响,用图像表示的话可能更为直观
全连接神经网络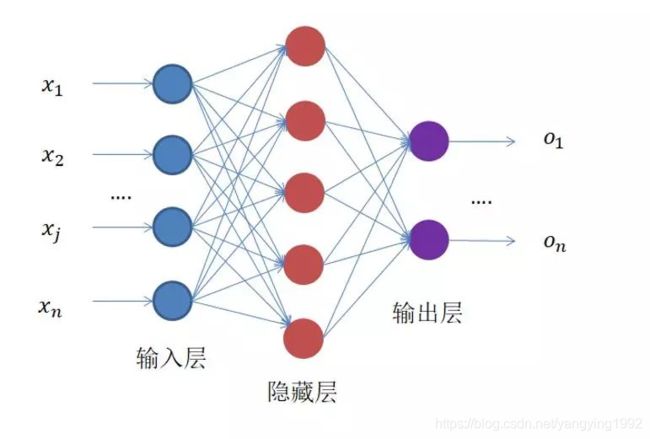
网络层分三大类:输入层,隐藏层和输出层。前一层的输出用作下一层的输入。在进行网络前向和后向学习之前,我们先对一些符号作出解释:
1、 w j k l w_{jk}^l wjkl表示第 l − 1 l-1 l−1层的第 k k k个节点对第 l l l层的第 j j j个节点的影响权重
2、 b j l b_j^l bjl表示第 l l l层的第 j j j个节点的偏置
3、 a j l a_j^l ajl表示第 l l l层的第 j j j个节点的激活输出
4、 z j l z_j^l zjl表示第 l l l层的第 j j j个节点的未激活输出
有了这四个符号以后,我们可以轻松地用数学公式描述网络的前向学习过程:
z j l = ∑ k w j k l a k l − 1 + b j l ⟶ 矢 量 化 为 : z l = w l a l − 1 + b l z_j^l=\sum_k{w_{jk}^la_k^{l-1}+b_j^l}\longrightarrow 矢量化为:z^l=w^la^{l-1}+b^l zjl=k∑wjklakl−1+bjl⟶矢量化为:zl=wlal−1+bl
设网络采用的激活函数为sigmoid,则第 l l l层的第 j j j个节点的激活输出为:
a j l = σ ( z j l ) = σ ( ∑ k w j k l a k l − 1 + b j l ) ⟶ 矢 量 化 为 : a l = σ ( w l a l − 1 + b l ) a_j^l=\sigma(z_j^l)=\sigma(\sum_k{w_{jk}^la_k^{l-1}+b_j^l})\longrightarrow矢量化为:a^l=\sigma(w^la^{l-1}+b^l) ajl=σ(zjl)=σ(k∑wjklakl−1+bjl)⟶矢量化为:al=σ(wlal−1+bl)
二、全连接神经网络的backpropagation
由前面的介绍可知,网络的最终输出为 a L a^L aL,其中 L L L为网络所包含的层数。假设网络的标准输出为 y y y,那么网络的后向学习过程其实就是通过不断地调整网络权重 w w w和偏置 b b b,使得网络输出 a L a^L aL更加地接近于标准输出 y y y。那么怎么样用数学语言描述 a L a^L aL和 y y y之间的接近程度呢?这里引入了loss函数。关于loss函数的选取其实也是网络搭建过程中需要考虑的问题之一,什么样的loss函数最好或者最适合也将是一个庞大的讨论课题,这里不再赘述。我们只以最简单的loss函数平方差为例作介绍。
C = 1 2 n ∑ j ∣ ∣ y j − a j L ∣ ∣ 2 C=\dfrac{1}{2n}\sum_j||y_j-a_j^L||^2 C=2n1j∑∣∣yj−ajL∣∣2
给出loss函数的定义以后我们需要弄明白一个问题,就是怎样调整权重 w w w和偏置 b b b的值才能使得网络的loss函数减小呢?这就涉及到了优化算法的问题,现在最常用的优化算法包括Adam,随机梯度下降法,AMSGrad等等,至于优化算法的选择也是一个可以展开研究的课题,这里不再赘述,直接给出结论,即朝着梯度的反方向调整权重和偏置的值可以求得loss函数的极值,不同的优化算法的区别主要也是集中于调整的学习率的选择。
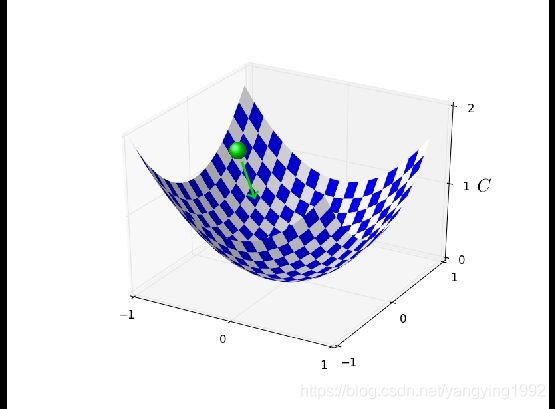
借用上面这张图我们作一个不算严谨的形象化的解释,我们都知道在极值点函数的导数为0,而非极值点的导数不为0,但是非极值点的梯度其实也表示出了整个函数值下降最快的方向,故而我们利用梯度来调整整个网络的权重和偏置,使得loss函数尽快向极值方向减小。后向传播算法就是寻求loss函数对应于网络中存在的各个权重 w w w以及偏置 b b b的偏导数,然后利用该偏导数调整整个网络的权重和偏置的过程。
在计算 ∂ C ∂ w j k l \dfrac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C和 ∂ C ∂ b j l \dfrac{\partial C}{\partial b_{j}^l} ∂bjl∂C之前,我们先引入一个中间变量,即 l l l层第 j j j个节点对应的偏导数 δ j l \delta_j^l δjl:
δ j l = ∂ C ∂ z j l \delta_j^l=\dfrac{\partial C}{\partial z_{j}^l} δjl=∂zjl∂C
方便起见,我们依然使用 δ l \delta^l δl来表示第 l l l层节点的偏导数,后向学习的过程其实就是计算网络中各个层的 δ l \delta^l δl,并将该 δ l \delta^l δl值关联到我们真正关心的权重 ∂ C ∂ w j k l \dfrac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C偏导和偏置 ∂ C ∂ b j l \dfrac{\partial C}{\partial b_{j}^l} ∂bjl∂C偏导上。
backpropagation(后向学习)有四个基础的公式,它们包含了怎样利用loss函数的值计算输出层偏导数,怎样利用 l + 1 l+1 l+1层的偏导数计算 l l l层偏导数,怎样利用网络层偏导数计算权重和偏置的偏导。下面我将具体来推导这四个基础公式。
公式1 输出层偏导数
loss函数对应于输出层各节点的未激活值偏导数 ∂ C ∂ z j L \dfrac{\partial C}{\partial z_{j}^L} ∂zjL∂C:
δ j L = ∂ C ∂ z j L \delta_j^L=\dfrac{\partial C}{\partial z_{j}^L} δjL=∂zjL∂C
根据链式法则得:
δ j L = ∑ k ∂ C ∂ a k L ∂ a k L ∂ z j L \delta_j^L=\sum_k\dfrac{\partial C}{\partial a_{k}^L}\dfrac{\partial a_k^L}{\partial z_j^L} δjL=k∑∂akL∂C∂zjL∂akL
而由于 z j L z_j^L zjL的值只影响到 a k L a_k^L akL的值,故而:
δ j L = ∂ C ∂ a j L ∂ a j L ∂ z j L \delta_j^L=\dfrac{\partial C}{\partial a_{j}^L}\dfrac{\partial a_j^L}{\partial z_j^L} δjL=∂ajL∂C∂zjL∂ajL
而 a j L = σ ( z j L ) a_j^L=\sigma (z_j^L) ajL=σ(zjL),故而我们得到后向学习的第一个公式:
δ j L = ∂ C ∂ a j L σ ′ ( z j L ) (nnBP.1) \delta_j^L=\dfrac{\partial C}{\partial a_{j}^L}\sigma'(z_j^L)\tag{nnBP.1} δjL=∂ajL∂Cσ′(zjL)(nnBP.1)
本身loss函数是关于 a j L a_j^L ajL和 y y y的函数,很容易求得 ∂ C ∂ a j L \dfrac{\partial C}{\partial a_{j}^L} ∂ajL∂C的值,比如当loss函数为平方差和时,我们有:
∂ C ∂ a j L = a j L − y j \dfrac{\partial C}{\partial a_{j}^L}=a_j^L-y_j ∂ajL∂C=ajL−yj
δ j L = ( a j L − y j ) σ ′ ( z j L ) \delta_j^L=(a_j^L-y_j)\sigma'(z_j^L) δjL=(ajL−yj)σ′(zjL)
公式二、 隐藏层偏导数
下面我们来推导第二个公式,即通过 l + 1 l+1 l+1层的偏导数 δ l + 1 \delta^{l+1} δl+1来获得第 l l l层的偏导数 δ l \delta^l δl,根据链式法则:
δ j l = ∂ C ∂ z j l = ∑ k ∂ C ∂ z k l + 1 ∂ z k l + 1 ∂ z j l = ∑ k δ k l + 1 ∂ z k l + 1 ∂ z j l \begin{aligned} \delta_j^l&=\dfrac{\partial C}{\partial z_j^l}\\&=\sum_k\dfrac{\partial C}{\partial z_k^{l+1}}\dfrac{\partial z_k^{l+1}}{\partial z_j^l}\\&=\sum_k\delta_k^{l+1}\dfrac{\partial z_k^{l+1}}{\partial z_j^l} \end{aligned} δjl=∂zjl∂C=k∑∂zkl+1∂C∂zjl∂zkl+1=k∑δkl+1∂zjl∂zkl+1
根据前向运算法则,我们有:
z k l + 1 = ∑ j w k j l + 1 a j l + b k l + 1 = ∑ j w k j l + 1 σ ( z j l ) + b k l + 1 \begin{aligned} z_k^{l+1}&=\sum_j w_{kj}^{l+1}a_j^l+b_k^{l+1}\\&=\sum_j w_{kj}^{l+1}\sigma(z_j^l)+b_k^{l+1} \end{aligned} zkl+1=j∑wkjl+1ajl+bkl+1=j∑wkjl+1σ(zjl)+bkl+1
将该结果代入到上式中,我们有:
δ j l = ∑ k δ k l + 1 ∂ ∑ j w k j l + 1 σ ( z j l ) + b k k + 1 ∂ z j l = ∑ k δ k l + 1 w k j l + 1 σ ′ ( z j l ) \begin{aligned} \delta_j^l&=\sum_k\delta_k^{l+1}\dfrac{\partial \sum_j w_{kj}^{l+1}\sigma(z_j^l)+b_k^{k+1}}{\partial z_j^l}\\&=\sum_k\delta_k^{l+1}w_{kj}^{l+1}\sigma'(z_j^l) \end{aligned} δjl=k∑δkl+1∂zjl∂∑jwkjl+1σ(zjl)+bkk+1=k∑δkl+1wkjl+1σ′(zjl)
即
δ j l = ∑ k w k j l + 1 δ k l + 1 σ ′ ( z j l ) (nnBP.2) \delta_j^l=\sum_kw_{kj}^{l+1}\delta_k^{l+1}\sigma'(z_j^l)\tag {nnBP.2} δjl=k∑wkjl+1δkl+1σ′(zjl)(nnBP.2)
这里我们就得到了后向学习的第二个公式。定义一个运算符 ⨀ \bigodot ⨀,表示两个向量的元素进行点乘,那么我们就可以将上述的nnBP.1和2写成下述的矢量表达形式:
δ L = ∇ a C ⨀ σ ′ ( z L ) (nnBP.1) \delta^L=\nabla_aC\bigodot\sigma'(z^L)\tag{nnBP.1} δL=∇aC⨀σ′(zL)(nnBP.1)
δ l = ( ( w l + 1 ) T δ l + 1 ) ⨀ σ ′ ( z l ) (nnBP.2) \delta^l=((w^{l+1})^T\delta^{l+1})\bigodot\sigma'(z^l)\tag{nnBP.2} δl=((wl+1)Tδl+1)⨀σ′(zl)(nnBP.2)
公式三四、权重和偏置对应的偏导数
有了这两个公式我们就可以求出网络各个节点对应于loss函数的偏导数,但是后向学习的过程其实是调整权重 w w w和偏置 b b b的过程,我们真正关心的应该是损失函数对应于权重和偏置的偏导数,下面我们来推导这两者的值。
对于权重 w j k l w_{jk}^l wjkl,其对应的损失函数偏导数:
∂ C ∂ w j k l = ∂ C ∂ z j l ∂ z j l ∂ w j k l = δ j l ∂ z j l ∂ w j k l \begin{aligned} \dfrac{\partial C}{\partial w_{jk}^l}&=\dfrac{\partial C}{\partial z_j^l}\dfrac{\partial z_j^l}{\partial w_{jk}^l}\\&=\delta_j^l\dfrac{\partial z_j^l}{\partial w_{jk}^l} \end{aligned} ∂wjkl∂C=∂zjl∂C∂wjkl∂zjl=δjl∂wjkl∂zjl
而根据前向运算公式:
z j l = ∑ k w j k l a k l − 1 + b j l z_j^l=\sum_kw_{jk}^la_k^{l-1}+b_j^l zjl=k∑wjklakl−1+bjl
故而:
∂ C ∂ w j k l = δ j l ∂ z j l ∂ w j k l = δ j l ∂ ∑ k w j k l a k l − 1 + b j l ∂ w j k l \begin{aligned} \dfrac{\partial C}{\partial w_{jk}^l}&=\delta_j^l\dfrac{\partial z_j^l}{\partial w_{jk}^l}\\&=\delta_j^l\dfrac{\partial \sum_kw_{jk}^la_k^{l-1}+b_j^l}{\partial w_{jk}^l} \end{aligned} ∂wjkl∂C=δjl∂wjkl∂zjl=δjl∂wjkl∂∑kwjklakl−1+bjl
简单计算可得:
∂ C ∂ w j k l = δ j l a k l − 1 (nnBP.3) \dfrac{\partial C}{\partial w_{jk}^l}=\delta_j^la_k^{l-1}\tag{nnBP.3} ∂wjkl∂C=δjlakl−1(nnBP.3)
同理可得:
∂ C ∂ b j l = δ j l (nnBP.4) \dfrac{\partial C}{\partial b_j^l}=\delta_j^l\tag{nnBP.4} ∂bjl∂C=δjl(nnBP.4)
此时我们得到了全连接神经网络后向学习相关的四个基础公式
三、卷积神经网络cnn
虽然利用全连接神经网络可以实现一些复杂的函数功能,但是真正推动神经网络发展的其实是卷积网络的出现。卷积网络实现了权重共享,在图像处理方面具有出色的优势。
下图显示了卷积神经网络的工作原理
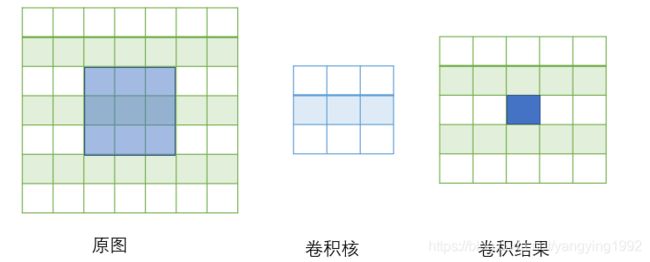
符号规则依然和全连接神经网络一样,那么卷基层的前向运算我们可以通过如下公式来表示:
z l ( x , y ) = ∑ a ∑ b σ ( z l ( x + a , y + b ) w l + 1 ( a , b ) + b l + 1 ) z^l(x,y)=\sum_a\sum_b\sigma(z^l(x+a,y+b)w^{l+1}(a,b)+b^{l+1}) zl(x,y)=a∑b∑σ(zl(x+a,y+b)wl+1(a,b)+bl+1)
卷积网络也真正地实现了权重共享,减少了网络搭建的参数。
卷积网络的backpropagation
对于卷积网络输出层的偏导数求解和全连接网络没有什么不同,我们就直接跳过。
我们直接来推导损失函数对于网络各层未激活输出的偏导数 δ l \delta^l δl,根据链式法则,我们有:
δ l ( x , y ) = ∂ C ∂ z l ( x , y ) = ∑ x ′ ∑ y ′ ∂ C ∂ z l + 1 ( x ′ , y ′ ) ∂ z l + 1 ( x ′ , y ′ ) ∂ z l ( x , y ) = ∑ x ′ ∑ y ′ δ l + 1 ( x ′ , y ′ ) ∑ a ∑ b σ ( z l ( x ′ + a , y ′ + b ) w l + 1 ( a , b ) + b l + 1 ) ∂ z l ( x , y ) = ∑ a ∑ b δ l + 1 ( x ′ , y ′ ) w l + 1 ( a , b ) σ ′ ( z l ( x , y ) ) \begin{aligned} \delta^l(x,y)&=\dfrac{\partial C}{\partial z^l(x,y)}\\&=\sum_{x'}\sum_{y'}\dfrac{\partial C}{\partial z^{l+1}(x',y')}\dfrac{\partial z^{l+1}(x',y')}{\partial z^l(x,y)}\\&=\sum_{x'}\sum_{y'}\delta^{l+1}(x',y')\dfrac{\sum_a\sum_b\sigma(z^l(x'+a,y'+b)w^{l+1}(a,b)+b^{l+1})}{\partial z^l(x,y)}\\&=\sum_{a}\sum_{b}\delta^{l+1}(x',y')w^{l+1}(a,b)\sigma'(z^l(x,y)) \end{aligned} δl(x,y)=∂zl(x,y)∂C=x′∑y′∑∂zl+1(x′,y′)∂C∂zl(x,y)∂zl+1(x′,y′)=x′∑y′∑δl+1(x′,y′)∂zl(x,y)∑a∑bσ(zl(x′+a,y′+b)wl+1(a,b)+bl+1)=a∑b∑δl+1(x′,y′)wl+1(a,b)σ′(zl(x,y))
其中 x = x ′ + a x=x'+a x=x′+a, y = y ′ + a y=y'+a y=y′+a,代入得:
δ l ( x , y ) = ∑ a ∑ b δ l + 1 ( x − a , y − b ) w l + 1 ( a , b ) σ ′ ( z l ( x , y ) ) \delta^l(x,y)=\sum_{a}\sum_{b}\delta^{l+1}(x-a,y-b)w^{l+1}(a,b)\sigma'(z^l(x,y)) δl(x,y)=a∑b∑δl+1(x−a,y−b)wl+1(a,b)σ′(zl(x,y))
令 a ′ = − a a'=-a a′=−a, b ′ = − b b'=-b b′=−b,我们有:
δ l ( x , y ) = ∑ a ∑ b δ l + 1 ( x + a ′ , y + b ′ ) w l + 1 ( − a ′ , − b ′ ) σ ′ ( z l ( x , y ) ) (cnnBP.1) \delta^l(x,y)=\sum_{a}\sum_{b}\delta^{l+1}(x+a',y+b')w^{l+1}(-a',-b')\sigma'(z^l(x,y))\tag{cnnBP.1} δl(x,y)=a∑b∑δl+1(x+a′,y+b′)wl+1(−a′,−b′)σ′(zl(x,y))(cnnBP.1)
我们得到了卷积运算后向学习过程的第一个公式,矢量化为:
δ l = δ l + 1 ∗ R O T 180 ( w l + 1 ) ⨀ σ ′ ( z l ) (cnnBP.1) \delta^l=\delta^{l+1}*ROT180(w^{l+1})\bigodot\sigma'(z^l)\tag{cnnBP.1} δl=δl+1∗ROT180(wl+1)⨀σ′(zl)(cnnBP.1)
得到卷基层各个分量对应于loss函数的偏导数以后,我们最关心的依然是学习过程中权重和偏置的调整,即权重 w w w和偏置 b b b对应于loss的偏导数,下面进行推导:
∂ C ∂ w l ( a , b ) = ∑ x ∑ y ∂ C ∂ z l ( x , y ) ∂ z l ( x , y ) ∂ w l ( a , b ) = ∑ x ∑ y δ l ( x , y ) ∂ z l ( x , y ) ∂ w l ( a , b ) = ∑ x ∑ y δ l ( x , y ) ∂ ∑ a ′ ∑ b ′ σ ( z l − 1 ( x + a ′ , y + b ′ ) ) w l ( a ′ , b ′ ) + b l ∂ w l ( a , b ) = ∑ x ∑ y δ l ( x , y ) σ ( z l − 1 ( x + a , y + b ) ) \begin{aligned} \dfrac{\partial C}{\partial w^l(a,b)}&=\sum_x\sum_y\dfrac{\partial C}{\partial z^l(x,y)}\dfrac{\partial z^l(x,y)}{\partial w^l(a,b)}\\&=\sum_x\sum_y\delta^l(x,y)\dfrac{\partial z^l(x,y)}{\partial w^l(a,b)}\\&=\sum_x\sum_y\delta^l(x,y)\dfrac{\partial \sum_{a'}\sum_{b'}\sigma(z^{l-1}(x+a',y+b'))w^l(a',b')+b^l}{\partial w^l(a,b)}\\&=\sum_x\sum_y\delta^l(x,y)\sigma(z^{l-1}(x+a,y+b)) \end{aligned} ∂wl(a,b)∂C=x∑y∑∂zl(x,y)∂C∂wl(a,b)∂zl(x,y)=x∑y∑δl(x,y)∂wl(a,b)∂zl(x,y)=x∑y∑δl(x,y)∂wl(a,b)∂∑a′∑b′σ(zl−1(x+a′,y+b′))wl(a′,b′)+bl=x∑y∑δl(x,y)σ(zl−1(x+a,y+b))
这里我们得到了卷积神经网络后向学习的第二个公式:
∂ C ∂ w l ( a , b ) = ∑ x ∑ y δ l ( x , y ) σ ( z l − 1 ( x + a , y + b ) ) (cnnBP.2) \dfrac{\partial C}{\partial w^l(a,b)}=\sum_x\sum_y\delta^l(x,y)\sigma(z^{l-1}(x+a,y+b))\tag{cnnBP.2} ∂wl(a,b)∂C=x∑y∑δl(x,y)σ(zl−1(x+a,y+b))(cnnBP.2)
矢量化为:
∂ C ∂ w l = δ l ∗ σ ( z l − 1 ) (cnnBP.2) \dfrac{\partial C}{\partial w^l}=\delta^l*\sigma(z^{l-1})\tag{cnnBP.2} ∂wl∂C=δl∗σ(zl−1)(cnnBP.2)
下面进行偏置的偏导数推导:
∂ C ∂ b l = ∑ x ∑ y ∂ C ∂ z l ( x , y ) ∂ z l ( x , y ) ∂ b l = ∑ x ∑ y δ l ( x , y ) ∂ z l ( x , y ) ∂ b l = ∑ x ∑ y δ l ( x , y ) ∂ ∑ a ′ ∑ b ′ σ ( z l − 1 ( x + a ′ , y + b ′ ) ) w l ( a ′ , b ′ ) + b l ∂ b l = ∑ x ∑ y δ l ( x , y ) \begin{aligned} \dfrac{\partial C}{\partial b^l}&=\sum_x\sum_y\dfrac{\partial C}{\partial z^l(x,y)}\dfrac{\partial z^l(x,y)}{\partial b^l}\\&=\sum_x\sum_y\delta^l(x,y)\dfrac{\partial z^l(x,y)}{\partial b^l}\\&=\sum_x\sum_y\delta^l(x,y)\dfrac{\partial \sum_{a'}\sum_{b'}\sigma(z^{l-1}(x+a',y+b'))w^l(a',b')+b^l}{\partial b^l}\\&=\sum_x\sum_y\delta^l(x,y) \end{aligned} ∂bl∂C=x∑y∑∂zl(x,y)∂C∂bl∂zl(x,y)=x∑y∑δl(x,y)∂bl∂zl(x,y)=x∑y∑δl(x,y)∂bl∂∑a′∑b′σ(zl−1(x+a′,y+b′))wl(a′,b′)+bl=x∑y∑δl(x,y)
这里我们得到了卷积神经网络后向学习的第三个公式:
∂ C ∂ b l = ∑ x ∑ y δ l ( x , y ) (cnnBP.3) \dfrac{\partial C}{\partial b^l}=\sum_x\sum_y\delta^l(x,y)\tag{cnnBP.3} ∂bl∂C=x∑y∑δl(x,y)(cnnBP.3)
至此我们得到了卷积网络后向学习的全部公式,至于现实中卷积核其实是 c h a n n e l i n p u t × k h × k w × c h a n n e l o u t p u t channel_{input}\times{k_h}\times{k_w}\times{channel_{output}} channelinput×kh×kw×channeloutput只是在原有的基础上增加一些简单的加减平均运算等,这里不作进一步推导。
完结