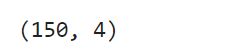- 1、机器学习概述
- 2、入门案例示例
- 3、问题定义
- 4、特征工程
- 4.1 数据理解
- 4.2 数据预处理
- 4.2.1 数据清洗
- 4.2.2 数据转换
- 4.2.3 特征选择
- 4.2.3.1 单变量特征选定:卡方检验(chi-squared)
- 4.2.3.2 递归特征消除:RFE
- 4.2.3.3 主要成分分析:PCA
- 4.2.3.4 特征重要性
- 5、模型选择
- 5.1 评估算法的方式
- 5.1.1 训练数据集和评估数据集分离
- 5.1.2 K折交叉验证分离
- 5.1.3 弃一交叉验证分离
- 5.1.4 重复随机分离评估数据集与训练数据集
- 5.2 评估算法的指标
- 5.2.1 分类准确度
- 5.2.2 对数损失函数
- 5.2.3 AUC图
- 5.2.4 混淆矩阵
- 5.2.5 分类报告
- 5.2.6 平均绝对误差
- 5.2.7 均方误差
- 5.2.8 决定系数
- 5.3 常用分类算法
- 5.4 常用回归算法
- 5.5 不同算法的比较
- 5.6 sklearn的Pipeline
- 5.1 评估算法的方式
- 6、模型优化
- 6.1 集成算法
- 6.1.1 袋装算法
- 6.1.2 提升算法
- 6.1.3 投票算法
- 6.2 算法调参
- 6.2.1 网格搜索优化参数
- 6.2.2 随机搜索优化参数
- 6.1 集成算法
- 7、模型部署
- 7.1 通过pickle序列化和反序列化机器学习模型
- 7.2 通过joblib序列化和反序列化机器学习模型
- 8、反馈跟踪
- 9、案例
- 9.1 问题定义
- 9.2 特征工程
- 9.3 模型选择
- 9.3.1 初步评估算法-原始数据
- 9.3.2 二次评估算法-正态化数据
- 9.4 模型优化
- 9.4.1 算法调参
- 9.4.2 使用集成算法
- 9.4.3 集成算法调参
- 9.5 确定最终模型
- 参考
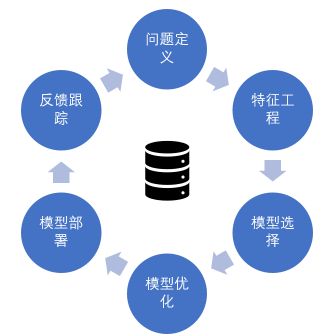
1、机器学习概述
-
问题定义
研究和提炼问题的特征,以帮助我们更好地理解项目的目标。
-
特征工程
-
数据理解
通过描述性统计和可视化来分析现有的数据质量和分布。
-
数据预处理
对数据进行预处理,特征选定,以便于构建一个预测模型。
-
-
模型选择
通过一定的方法分离一部分数据,用来评估算法模型,并选取一部分代表数据进行分析,以改善模型。
-
模型优化
通过调参和集成算法提升预测结果的准确度。
-
模型部署
完成模型,并执行模型来预测结果和展示。
-
反馈跟踪
收集反馈结果,做正负向调节
2、入门案例示例
-
导入基本包:
import pandas as pd import numpy as np import matplotlib.pyplot as plt -
导入数据:
# 导入数据 from sklearn.datasets import load_iris iris = load_iris() data_X = pd.DataFrame(iris.data,columns=iris.feature_names) data_y = iris.target -
查看数据维度:
# 查看数据的维度 data_X.shape -
查看数据自身:
# 查看数据自身 data_X.head(5) -
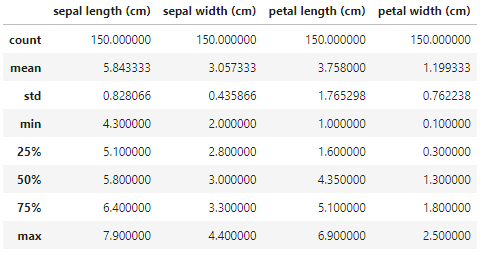
统计描述数据:
# 统计描述数据 data_X.describe() -
数据分类分布:
# 数据分类分布 for i in np.unique(data_y): print("{}:".format(i),sum(data_y==i)) -
单变量图表:
-
多变量图表:
-
评估算法:
-
分离数据集
# 分离数据集 from sklearn.model_selection import train_test_split validation_size = 0.2 seed = 7 X_train,X_validation,Y_train,Y_validation = train_test_split(data_X,data_y,test_size=validation_size,random_state=seed) -
评估模式
# 评估模式 from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score # 导入算法模型 # 线性算法 from sklearn.linear_model import LogisticRegression # LR from sklearn.discriminant_analysis import LinearDiscriminantAnalysis # LDA # 非线性模型 from sklearn.tree import DecisionTreeClassifier # CART from sklearn.neighbors import KNeighborsClassifier # KNN from sklearn.naive_bayes import GaussianNB # NB from sklearn.svm import SVC # SVM # 设置随机数种子 seed = 7 # 装载算法 models = dict() models["LR"] = LogisticRegression() models["LDA"] = LinearDiscriminantAnalysis() models["KNN"] = KNeighborsClassifier() models["CART"] = DecisionTreeClassifier() models["NB"] = GaussianNB() models["SVM"] = SVC() # 评估算法 results = [] for key in models: kfold = KFold(n_splits=10,random_state=seed,shuffle=True) cv_results = cross_val_score(models[key],X_train,Y_train,cv=kfold,scoring="accuracy") results.append(cv_results) print("{}:{} {}".format(key,cv_results.mean(),cv_results.std())) -
箱线图比较算法效果
# 箱线图比较算法 fig = plt.figure() fig.suptitle("Algorithm Comparison") ax = fig.add_subplot(111) plt.boxplot(results) ax.set_xticklabels(models.keys()) plt.show()
-
-
实施预测
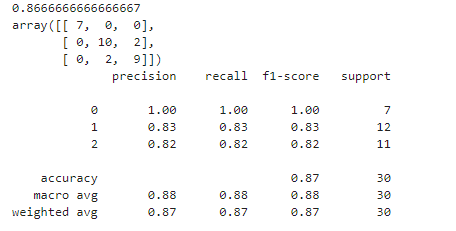
# 导入评估包 from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score from pprint import pprint # 使用评估数据集评估算法 svm = SVC() svm.fit(X=X_train,y=Y_train) predictions = svm.predict(X_validation) pprint(accuracy_score(Y_validation,predictions)) pprint(confusion_matrix(Y_validation,predictions)) print(classification_report(Y_validation,predictions))
3、问题定义
三个W:
- 数据挖掘的对象是什么——who
- 数据挖掘的商业目的——what
- 数据挖掘要解决的业务问题——why
4、特征工程
4.1 数据理解
import pandas as pd
filename = "..."
dataframe = pd.DataFrame(filename)-
查看数据的表现形式
dataframe.head(10) -
查看数据的维度
# 展示数据行和列 dataframe.shape -
查看数据的属性和类型
# 展示数据的类型 dataframe.dtypes -
描述性统计
https://www.cnblogs.com/nuochengze/p/15725751.html#autoid-2-0-3
# 数据记录数、平均值、标准方差、最小值、下四分位数、中位数、上四分位数、最大值 dataframe.describe()-
数据的集中趋势
-
数据的离中趋势
-
数据分组分布
# 查看数据分布是否均衡 dataframe.groupby("column_name").size()
-
-
数据属性的相关性
https://www.cnblogs.com/nuochengze/p/15725751.html#autoid-6-1-2
# 按Pearson相关系数表示两个变量间的相关程度 dataframe.corr(method="pearson") -
数据的分布分析
https://www.cnblogs.com/nuochengze/p/15725751.html#autoid-3-1-4
# 通过数据的高斯分布情况来确认数据的偏离程度 data.skew()skew()函数的结果显示了数据分布是左偏还是右偏,当数据接近0时,表示数据的偏差非常小。
-
数据图表展示
https://www.cnblogs.com/nuochengze/p/15725751.html#autoid-2-6-0
-
单一图表
-
直方图
横轴表示数据类型,纵轴表示分布情况。
通过直方图,直观查看数据是高斯分布、指数分布还是偏态分布。
dataframe.hist() -
密度图
dataframe.plot(kind="density",subplots=True,layout=(2,2),sharex=False,sharey=False,grid=True,figsize=(8,8)) -
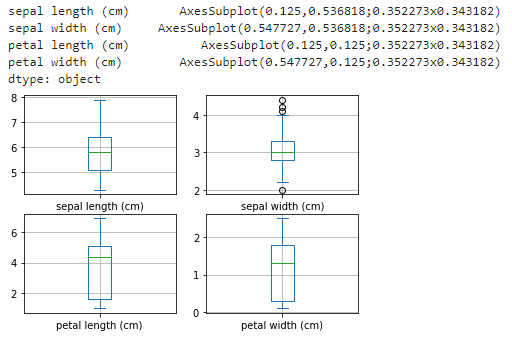
箱线图
dataframe.plot(kind="box",subplots=True,layout=(2,2),sharex=False,sharey=False,grid=True)
-
-
多重图表
-
相关矩阵图
相关矩阵图用来展示两个不同属性互相影响的程度。
import matplotlib.pyplot as plt import seaborn as sns # 方法一: fig = plt.figure() ax = fig.add_subplot(111) cax = ax.matshow(dataframe.corr(),vmin=-1,vmax=1) fig.colorbar(cax) ax.set_xticks(np.arange(0,len(dataframe.columns),1)) ax.set_yticks(np.arange(0,len(dataframe.columns),1)) ax.set_xticklabels(dataframe.columns) ax.set_yticklabels(dataframe.columns) # 方法二: fig = plt.figure() ax = fig.add_subplot(111) sns.heatmap(datafarme.corr(),annot=True,cmap="rainbow",ax=ax, annot_kws={ "size":12, "weight":"bold", "color":"blue" }) plt.xticks(rotation=30) -
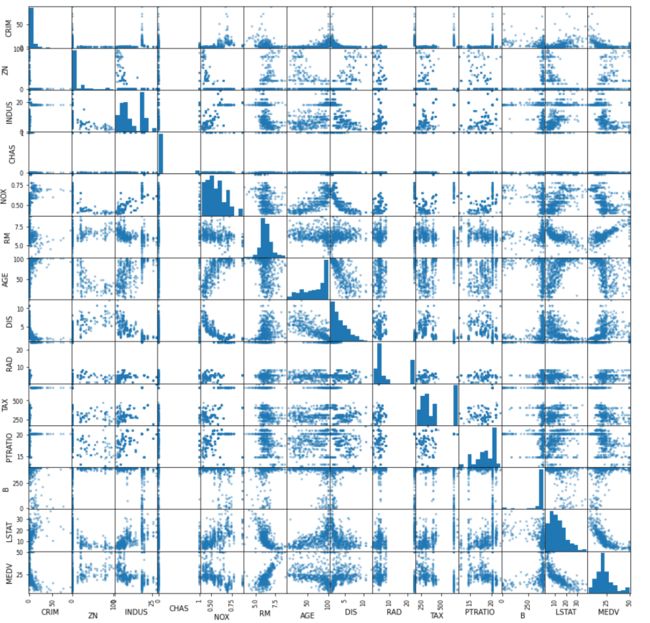
散点矩阵图
散点矩阵图表示因变量随自变量变化的大致趋势,可以判断两个变量之间是否存在某种关联或总结坐标点的分布模式。
from pandas.plotting import scatter_matrix scatter_matrix(data)
-
-
4.2 数据预处理
数据预处理可分为三个步骤:数据清洗、数据转换、特征选择。
4.2.1 数据清洗
https://www.cnblogs.com/nuochengze/p/12426527.html
4.2.2 数据转换
scikit-learn提供两种标准的格式化数据的方法:
-
Fit and Multiple Transform
先调用fit()函数来准备数据转换的参数,然后调用transform()函数来做数据的预处理。
-
Combined Fit-and-Transform
-
调整数据尺度
通过MinMaxScaler类来调整数据尺度,将属性缩放到一个指定范围,或者对数据进行标准化并将数据都聚集到0附近,方差为1。
from sklearn.datasets import load_iris import pandas as pd from sklearn.preprocessing import MinMaxScaler iris = load_iris() data = pd.DataFrame(iris.data,columns=iris.feature_names) transformer = MinMaxScaler(feature_range=(0,1)) new_data = transformer.fit_transform(data) pd.DataFrame(new_data,columns=iris.feature_names).describe() -
正态化数据
正态化数据,假定数据符合高斯分布,输出为以0为中位数,方差为1的数据。
from sklearn.datasets import load_iris import pandas as pd from sklearn.preprocessing import StandardScaler iris = load_iris() data = pd.DataFrame(iris.data,columns=iris.feature_names) transformer = StandardScaler().fit(data) newData = transformer.transform(data) pd.DataFrame(newData,columns=iris.feature_names).describe() -
标准化数据
标准化数据,将每一行的数据的距离处理成1(即线性代数中矢量距离为1)的数据,又称为"归一元"处理,适合处理稀疏数据。
from sklearn.datasets import load_iris import pandas as pd from sklearn.preprocessing import Normalizer iris = load_iris() data = pd.DataFrame(iris.data,columns=iris.feature_names) transformer = Normalizer().fit(data) newData = transformer.transform(data) pd.DataFrame(newData,columns=iris.feature_names).describe() -
二值数据
二值化数据,是指将数据转化为二值,大于阈值设置为1,小于阈值设置为0,又称为二分数据或阈值转换。
from sklearn.datasets import load_iris import pandas as pd from sklearn.preprocessing import Binarizer iris = load_iris() data = pd.DataFrame(iris.data,columns=iris.feature_names) # threshold为阈值选项 transformer = Binarizer(threshold=3).fit(data) newData = transformer.transform(data) pd.DataFrame(newData,columns=iris.feature_names).describe()
4.2.3 特征选择
特征选择的作用:
-
降低数据的拟合度
较少的冗余数据,会使算法得出结论的机会更大
-
提高算法精度
较少的误导数据,能够提高算法的准确度
-
减少训练时间
越少的数据,训练模型所需要的时间越少
4.2.3.1 单变量特征选定:卡方检验(chi-squared)
卡方检验的定义:
经典的卡方检验是检验定性自变量对定性因变量的相关性的方法,假设自变量有$$N$$种取值,因变量有$$M$$种取值,考虑自变量等于$$i$$且应变量等于$$j$$的样本频数的观察值与期望值的差距,构成统计量。
即卡方检验是统计样本的实际观测值与理论推断值之间的偏离程度,偏离程度决定了卡方值的大小:
- 卡方值越大,越不符合;
- 卡方值越小,偏差越小,越趋于符合;
- 若两个值完全相等,卡方值就为0,表明理论值完全符合
scikit-learn中提供了SelectBest类,有对卡方检验的实现,通过这一系列统计方法,可以用来分析和选择对结果影响最大的数据特征。
from pandas import read_csv
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris.data,columns=iris.feature_names)
selectkbest = SelectKBest(score_func=chi2,k=2)
selectkbest.fit(data,iris.target)
# 获取得分
print("selectkbest.scores_:",selectkbest.scores_)
# 获取选定的特征
features = selectkbest.transform(data)
features[:10]获取得分最高的2个数据特征:
说明:
设置SelectKBest的score_func参数,SelectKBest不仅可以执行卡方检验来选择数据特征,还可以通过相关系数、互信息法等统计方法来选定数据特征。
4.2.3.2 递归特征消除:RFE
说明:
递归特征消除(RFE)使用一个基模型来进行多轮训练,每轮训练后消除若干权值系数的特征,再基于新的特征集进行下一轮训练,通过每一个基模型的精度,找到对最终的预测结果影响最大的数据特征。
import pandas as pd
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
# 以逻辑回归算法为基模型,通过递归特征消除来选定对预测结果影响最大的三个数据特征
iris = load_iris()
X = pd.DataFrame(iris.data,columns=iris.feature_names)
Y = iris.target
model = LogisticRegression()
rfe = RFE(estimator=model,n_features_to_select=3)
fit = rfe.fit(X,Y)
print("特征个数:",fit.n_features_)
print("被选定的特征:",fit.support_)
print("特征排名:",fit.ranking_)被选中的特征再support_中被标记为True,在ranking_中被标记为1
4.2.3.3 主要成分分析:PCA
说明:
主要成分分析(PCA)使用线性代数来转换压缩数据,通常被称为数据降维。
扩展:
常见的降维方法除了主要成分分析(PCA),还有线性判别分析(LDA),PCA和LDA其本质都是将原始的样本映射到维度更低的样本空间中;但是PCA和LDA的映射目标有区别:PCA是为了让映射后的样本具有最大的发散性,而LDA是为了让映射后的样本有最好的分类性能(LDA本身也是一个分类模型)。PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
pca = PCA(n_components=2)
fit = pca.fit(X)
print("解释方差:",fit.explained_variance_ratio_)
print("主要成分:\n")
fit.components_![]()
4.2.3.4 特征重要性
说明:
袋装决策树算法(Bagged Decision Tress)、随机森林算法和极端随机数算法都可以用来计算数据特征的重要性。
import pandas as pd
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
model = ExtraTreesClassifier()
fit = model.fit(X,Y)
# 显示特征的重要性
fit.feature_importances_5、模型选择
5.1 评估算法的方式
5.1.1 训练数据集和评估数据集分离
通过sklearn.model_selection.train_test_split快速的将数据进行切割
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
test_size = 0.3
seed = 4
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed)
print("X.shape:",X.shape)
print("X_train.shape",X_train.shape)说明:
- test_size指定了测试数据分离的大小。
- seed指定了数据随机的粒度(seed=4),可以确保每次执行程序得到相同的结果。
- 为了保证算法比较是在相同的条件下执行的,必须保证训练数据集和评估数据集是相同的。
5.1.2 K折交叉验证分离
交叉验证:
交叉验证是用来验证分类器的性能的一种统计分析方法,基本思想是按照某种规则将原始数据进行分组,一部分作为训练数据集,另一部分作为评估数据集,首先用训练数据集对分类器进行训练,再利用评估数据集来测试训练得到的模型,以此作为评价分类器的性能指标。
K折交叉验证:
K折交叉验证是将原始数据分成K组(一般是均分),将每个子集数据分别做一次验证集,其他的K-1组子集数据作为训练集,这样会得到K个模型,再用这K个模型最终的验证集的分类准确率的平均数,作为此K折交叉验证下分类器的性能指标。
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression()
result = cross_val_score(model,X,Y,cv=kfold)
print("算法评估结果: \n 评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.1.3 弃一交叉验证分离
弃一交叉验证分离:
如果原始数据有N个样本,那么弃一交叉验证就是N-1个交叉验证,即每个样本单独作为验证集,其余的N-1个样本作为训练集,所以弃一交叉验证会得到N个模型,用这N个模型最终的验证集的分类准确率的平均数作为此弃一交叉验证分类器的性能指标。
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
leaveoneout = LeaveOneOut()
model = LogisticRegression()
result = cross_val_score(model,X,Y,cv=leaveoneout)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.1.4 重复随机分离评估数据集与训练数据集
重复随机分离评估数据集与训练数据集:
这是K折交叉验证的另外一种用途,其会重复这个过程多次,如同交叉验证分离。
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
# 将数据按照7:3的比例分离,然后重复这个过程10次
n_splits=10
test_size=0.3
seed=7
kfold = ShuffleSplit(n_splits=n_splits,test_size=test_size,random_state=seed)
model = LogisticRegression()
result = cross_val_score(model,X,Y,cv=kfold)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2 评估算法的指标
| 分类算法评估指标 | 回归算法评估指标 |
|---|---|
| 分类准确度 | 平均绝对误差(MAE) |
| 对数损失函数(Logloss) | 均方误差(MSE) |
| AUC图 | 决定系数($$R^{2}$$) |
| 混淆矩阵 | |
| 分类报告 |
5.2.1 分类准确度
说明:
分类准确度就是算法自动分类正确的样本数除以所有的样本数得出的结果。
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
num_folds = 10
seed=7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression()
result = cross_val_score(model,X,Y,cv=kfold)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2.2 对数损失函数
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
Y = iris.target
num_folds = 10
seed=7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression()
# 定义对数损失函数
scoring = "neg_log_loss"
result = cross_val_score(model,X,Y,cv=kfold,scoring=scoring)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2.3 AUC图
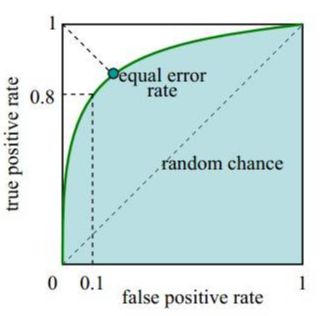
ROC和AUC都是评价分类器的指标。
ROC:
ROC是受试者工作特征曲线(Receiver Operating Characteristic Curve)的简写,又称为感受性曲线(Sensitivity Curve)。ROC是反映敏感性和特异性连续变量的综合指标,用构图法揭示敏感性和特异性的相互关系,通过将连续变量设定出多个不同的临界值计算出一系列敏感性和特异性,再以敏感性为纵坐标,(1-特异性)为横坐标绘制成曲线。
AUC:
AUC是ROC曲线下的面积(Area Under ROC Curve)的简称,AUC的值就是处于ROC Curve下方的那部分面积的大小。通常AUC的值介于0.5到1.0之间,AUC的值越大,诊断准确定性越高。
在ROC曲线上,靠近坐标图左上方的点为敏感性和特异性均较高的临界值。
通过二分类问题,理解ROC的概念:
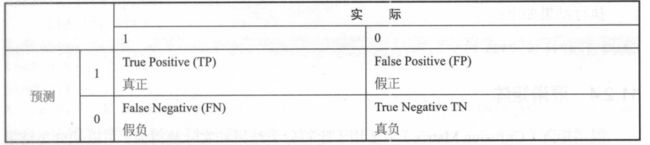
二分类混淆矩阵如下(“1”代表正类,“0”代表负类):
将实例分成 正类(Positive)或负类(Negative),存在四种情况:
- 如果一个实例是正类并且也被预测成正类,称为真正类(True Positive)
- 如果一个实例是负类却被预测成正类,称为假正类(False Positive)
- 如果一个实例是负类并且也被预测成负类,称为真负类(True Negative)
- 如果一个实例为正类却被预测成负类,称为假负类(False Negative)
数值计算公式:
-
敏感性指标(Sensitivity),又称为真正类率(True Positive Rate,TPR)
定义:分类器所识别出的正实例占所有正实例的比例
公式:$$TPR = \frac{TP}{TP+FN} $$
-
特异性指标(Specificity),又称为真负类率(True Negative Rate,TNR)
定义:分类器所识别出的负实例占所有负实例的比例
公式:$$TNR=\frac{TN}{TN+FP}=1-FPR$$
-
负正类率(False Positive Rate,FPR)
定义:分类器错认为正类的负实例占所有负实例的比例
公式:$$FPR=\frac{FP}{TN+FP}$$
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X = iris.data
Y = iris.target
seed=7
num_folds = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression()
# ROC
scoring = 'roc_auc'
result = cross_val_score(model,X,Y,cv=kfold,scoring=scoring)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2.4 混淆矩阵
作用:
混淆矩阵(Confusion Matrix)主要用于比较分类结果和实际测得值,可以把分类结果的精度显示在一个混淆矩阵中。
说明:
混淆矩阵的每列代表预测类别,每列的总数表示预测为该类别的数据的数目
混淆矩阵的每行代表真实归属类别,每行的数据总数表示该类别的数据的数目,每列中的数值表示真实数据被预测为该类的数据。
图例:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
import pandas as pd
iris = load_iris()
X = iris.data
Y = iris.target
seed = 7
test_size = 0.3
train_X,test_X,train_Y,test_Y = train_test_split(X,Y,test_size=test_size,random_state=seed)
model = LogisticRegression()
model.fit(train_X,train_Y)
predicted = model.predict(test_X)
matrix = confusion_matrix(test_Y,predicted)
# 获取分类的类别
classes = pd.unique(iris.target)
dataframe = pd.DataFrame(data=matrix,index=classes,columns=classes)
dataframe5.2.5 分类报告
说明:
分类报告,是对分类问题的评估报告,能够给出 精确率(Precision)、召回率(Recall)、F1值(F1-Score)和样本数目(support)。
通过二分类问题,理解分类报告的概念:
-
精确率
定义:所有分类中,预测为真正类且正确的数目 与 所有被预测为正类的数目的总和 的占比。
公式:$$P=\frac{TP}{TP+FP}$$
-
召回率
定义:所有分类中,预测为真正类且正确的数目 与 所有实际为正类的数据的总和 的占比。
公式:$$R=\frac{TP}{TP+FN}$$
-
F1值
定义:F1值就是精确率和召回率的调和均值。
公式:$$F1=\frac{P+R}{2}$$
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
import pandas as pd
iris = load_iris()
X = iris.data
Y = iris.target
seed = 7
test_size = 0.3
train_X,test_X,train_Y,test_Y = train_test_split(X,Y,test_size=test_size,random_state=seed)
model = LogisticRegression()
model.fit(train_X,train_Y)
predicted = model.predict(test_X)
report = classification_report(test_Y,predicted)
print(report)5.2.6 平均绝对误差
说明:
平均绝对误差(Mean Absolute Error,MAE)是所有单个观测值与算术平均值的偏差的绝对值的平均值。
与平均误差相比,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,所以平均绝对误差能更好地反映预测值误差的实际情况。
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
iris = load_iris()
X = iris.data
Y = iris.target
n_splits=10
seed=7
kfold = KFold(n_splits=n_splits,random_state=7,shuffle=True)
model = LinearRegression()
# 平均绝对误差
scoring = "neg_mean_absolute_error"
result = cross_val_score(model,X,Y,cv=kfold,scoring=scoring)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2.7 均方误差
说明:
均方误差(Mean Squared Error,MSE),是衡量平均误差的方法,可以评价数据的变化程度,均方根误差是均方误差的算术平方根,均方误差的值越小,说明用该预测模型描述实验数据的准确度越高。
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
iris = load_iris()
X = iris.data
Y = iris.target
n_splits=10
seed=7
kfold = KFold(n_splits=n_splits,random_state=7,shuffle=True)
model = LinearRegression()
# 均方误差
scoring = "neg_mean_squared_error"
result = cross_val_score(model,X,Y,cv=kfold,scoring=scoring)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.2.8 决定系数
说明:
决定系数,反映因变量的全部变异能通过回归关系被自变量解释的比例。
拟合优度越大,自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比越高,观察点在回归直线附近越密集。
决定系数($$R^{2}$$)的特点:
1.可决系数是非负的统计量
2.可决系数的取值范围为:0≤$$R^{2}$$≤1
3.可决系数是样本观测值的函数,是因随机抽样而变动的随机变量,因此需要对可决系数的统计的可靠性进行检验
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
iris = load_iris()
X = iris.data
Y = iris.target
n_splits=10
seed=7
kfold = KFold(n_splits=n_splits,random_state=7,shuffle=True)
model = LinearRegression()
scoring = "r2"
result = cross_val_score(model,X,Y,cv=kfold,scoring=scoring)
print("算法评估结果: \n评估的得分:{},标准方差:{}".format(round(result.mean(),3),round(result.std(),3)))5.3 常用分类算法
-
线性
逻辑回归:LR
线性判别分析:LDA
-
非线性
K近邻 :KNN
贝叶斯分类器
分类与回归树:CART
支持向量机:SVM
5.4 常用回归算法
-
线性
线性回归
岭回归(脊回归)
套索回归
弹性网络回归
-
非线性
K近邻:KNN
分类与回归树:CART
支持向量机:SVM
5.5 不同算法的比较
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
import matplotlib.pyplot as plt
# 排除警告
import warnings
warnings.filterwarnings("ignore")
# 准备数据
X = iris.data
Y = iris.target
# 10折交叉验证
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
# 装载模型
models = dict()
models["LR"] = LogisticRegression()
models["LDA"] = LinearDiscriminantAnalysis()
models["KNN"] = KNeighborsClassifier()
models["CART"] = DecisionTreeClassifier()
models["SVM"] = SVC()
models["NB"] = GaussianNB()
results = list()
# 存储结果
for key in models:
result = cross_val_score(models[key],X,Y,cv=kfold)
results.append(result)
print("%s: %.3f %.3f" %(key,result.mean(),result.std()))
# 箱线图展示结果
fig = plt.figure()
ax = fig.add_subplot(111)
fig.suptitle("Algorithm Comparison")
plt.boxplot(results)
ax.set_xticklabels(models.keys())
plt.show()5.6 sklearn的Pipeline
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.pipeline import FeatureUnion
from sklearn.pipeline import Pipeline
import warnings
warnings.filterwarnings("ignore")
iris = load_iris()
X = iris.data
Y = iris.target
num_fold = 10
seed = 7
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 准备FeatureUnion
features = list()
# 通过主成分进行特征选择
features.append(("pca",PCA()))
# 通过统计方法选择特征
features.append(("select_best",SelectKBest(k=3)))
# 生成Pipeline
steps = list()
steps.append(("feature_union",FeatureUnion(features)))
steps.append(("logistic",LogisticRegression()))
# 准备模型
model = Pipeline(steps)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()6、模型优化
6.1 集成算法
6.1.1 袋装算法
说明:
袋装算法(Bagging):先将训练集分离成多个子集,然后通过各个子集训练多个模型,以给定组合投票的方式获得最优解。
袋装算法在数据具有很大的方差时非常有效。
常用袋装模型:
| 袋装模型 |
|---|
| 袋装决策树(Bagged Decision Trees) |
| 随机森林(Random Forest) |
| 极端随机数(Extra Trees) |
极端随机树和随机森林的区别:
- 随机森林应用的是Bagging模型,而极端随机数是使用所有的训练样本得到每颗决策树,即每颗决策树应用的是相同的全部训练样本。
- 随机森林是在一个随机子集内得到最优分叉特征属性,而极端随机数是完全随机地选择分叉特征属性,从而实现对决策树进行分叉的。
袋装决策树:
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
# 导入数据
iris = load_iris()
X = iris.data
Y = iris.target
# 10折交验证
num_fold = 10
seed = 4
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 声明树模型
cart = DecisionTreeClassifier()
# 创建的树数量
num_tree = 100
# 创建袋装决策树模型
model = BaggingClassifier(base_estimator=cart,
n_estimators=num_tree,
random_state=seed)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()随机森林决策树:
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
# 导入数据
iris = load_iris()
X = iris.data
Y = iris.target
# 10折交验证
num_fold = 10
seed = 4
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 创建的树数量
num_tree = 100
# 最大特征数
max_features = 3
# 声明随机森林树模型
model = RandomForestClassifier(n_estimators=num_tree,
random_state=seed,
max_features=max_features)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()极端随机树:
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifier
# 导入数据
iris = load_iris()
X = iris.data
Y = iris.target
# 10折交验证
num_fold = 10
seed = 4
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 创建的树数量
num_tree = 100
# 最大特征数
max_features = 3
# 声明随机极端树模型
model = ExtraTreesClassifier(n_estimators=num_tree,
random_state=seed,
max_features=max_features)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()6.1.2 提升算法
说明:
提升算法(Boosting):训练多个模型并组成一个序列,序列中的每一个模型都会修正前一个模型的错误。
原理:将其他的弱分类算法作为基分类算法放于提升框架中,通过提升框架对训练样本集进行操作生成不同的训练样本子集,再用该样本子集去训练生成基分类器,即每得到一个样本集就用该基分类算法在该样本集上产生一个基分类器,这样在给定训练轮数n后,就可产生n个基分类器,然后提升算法将这n个基分类器进行加权融合,产生最后的结果分类器。
常用提升模型:
| 提升模型 |
|---|
| AdaBoost |
| 随机梯度提升(Stochastic Gradient Boosting) |
AdaBoost:
AdaBoost算法,其本身通过改变数据分布来实现,它根据每次训练集中每个样本的分类是否正确,以及上次的总体分类的准确率,来确定每个样本的权值,将修改过权值的新数据集送给下层分类器进行训练,再将每次训练得到的分类器融合起来,作为最后的决策分类器。
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifier
# 导入数据
iris = load_iris()
X = iris.data
Y = iris.target
# 10折交验证
num_fold = 10
seed = 4
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 创建的树数量
num_tree = 100
# 最大特征数
max_features = 3
# 声明树模型
model = AdaBoostClassifier(n_estimators=num_tree,
random_state=seed)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()随机梯度提升:
梯度提升法(GBM)基于的思想:要找到某个函数的最大值,最好的办法就是沿着该函数的梯度方向探寻,其梯度算子总是指向函数值增长最快的方向。
由于梯度提升算法在每次更新数据集时都需要遍历整个数据集,计算复杂度搞,于是改进为随机梯度提升算法,该算法一次只用一个样本点来更新回归系数,极大地改善了算法的计算复杂度。
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifier
# 导入数据
iris = load_iris()
X = iris.data
Y = iris.target
# 10折交验证
num_fold = 10
seed = 4
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
# 创建的树数量
num_tree = 100
# 最大特征数
max_features = 3
# 声明树模型
model = GradientBoostingClassifier(n_estimators=num_tree,
random_state=seed)
result = cross_val_score(model,X,Y,cv=kfold)
result.mean()6.1.3 投票算法
投票算法(Voting):通过创建多个算法模型,利用投票算法将这些算法包装起来,计算各个子模型的平均预测状况。
from sklearn.datasets import load_iris
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import VotingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
import warnings
warnings.filterwarnings("ignore")
iris = load_iris()
X = iris.data
Y = iris.target
num_fold = 10
seed = 5
kfold = KFold(n_splits=num_fold,random_state=seed,shuffle=True)
models = list()
models.append(("logistic",LogisticRegression()))
models.append(("cart",DecisionTreeClassifier()))
models.append(("svm",SVC()))
# 包装多个算法模型
ensemble_model = VotingClassifier(estimators=models)
result = cross_val_score(ensemble_model,X,Y,cv=kfold)
result.mean()6.2 算法调参
说明:
机器学习的模型都是参数化的,可以通过调参来提高模型的准确度,即超参数优化。
参数可分为两种:
1.影响模型在训练集上的准确度或防止过拟合能力的参数
2.不影响模型在训练集上的准确度或防止过拟合能力的参数
6.2.1 网格搜索优化参数
说明:
网格搜索优化参数是一种算法参数优化的方法,它通过遍历已定义参数的列表,来评估算法的参数,从而找到最优参数。
网格搜索优化参数适用于三四个或更少的超参数(如果超参数的数量增加,网格搜索的计算复杂度会呈现指数型增长,需要更换为随机搜索优化参数)。
由使用者列出一个较小的超参数值域,这些超参数值域的笛卡尔积(排列组合)为一组组超参数,网格搜索算法使用每组超参数训练模型,并挑选验证集误差最小的超参数组合。
scikit中使用GridSearchCV来实现对参数的跟踪、调整与评估,从而找到最优参数。
GridSearchCV使用字典对象来指定需要调参的参数,可以同时对一个或多个参数进行调参。
from sklearn.datasets import load_iris
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
iris = load_iris()
X = iris.data
Y = iris.target
model = Ridge()
# 设置要遍历的参数
param_grid = {
"alpha":[1,0.1,0.01,0.001,0]
}
# 通过网格搜索查询最优参数
"""
param_grid是一个字典对象,以算法的参数名为Key,需要遍历的参数值列表为value,
在验证算法最优参数的网格搜索算法中,可以设定多个Key:value对,同时查询多个参数的最优参数值
"""
grid = GridSearchCV(model,param_grid=param_grid)
grid.fit(X,Y)
print("最高得分:%.3f" % grid.best_score_)
print("最优参数:%s" % grid.best_estimator_.alpha)6.2.2 随机搜索优化参数
说明:
随机搜索优化参数通过固定次数的迭代,采用随机采样分布(随机搜索优化参数为每个参数定义了一个分布函数,并在该空间中采样)的方式搜索合适的参数。
from sklearn.datasets import load_iris
from sklearn.linear_model import Ridge
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform
iris = load_iris()
X = iris.data
Y = iris.target
model = Ridge()
param_grid = {"alpha":uniform()}
# 设置迭代次数
num_iter = 100
seed = 7
grid = RandomizedSearchCV(model,param_distributions=param_grid,n_iter=num_iter,random_state=seed)
grid.fit(X,Y)
print("最高得分:%.3f" % grid.best_score_)
print("最优参数:%s" % grid.best_estimator_.alpha)7、模型部署
说明:
模型在部署的过程中,注意Python的版本号,序列化模型和反序列化模型时,需要使用相同的Python版本。
模型在部署的过程中,需要记录所有的主要类库的版本。
7.1 通过pickle序列化和反序列化机器学习模型
说明:
pickle是标准的python序列化的方法,可以通过它来序列化机器学习算法生成的模型,并将其保存到文件中。
当需要对新数据进行预测时,将保存在文件中的模型反序列化,并用其来预测新数据的结果。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import pickle
# 加载数据
iris = load_iris()
X = iris.data
Y = iris.target
# 切割数据
test_size = 0.3
seed = 7
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed)
# 训练模型
model = LogisticRegression()
model.fit(X_train,Y_train)
# 保存模型
model_file = "./finalized_model.sav"
with open(model_file,"wb") as f:
# 序列化模型
pickle.dump(model,f)
# 加载模型
with open(model_file,"rb") as f:
# 反序列化模型
loaded_model = pickle.load(f)
result = loaded_model.score(X_test,Y_test)
result7.2 通过joblib序列化和反序列化机器学习模型
说明:
通过joblib序列化对象时会采用Numpy的格式保存数据,这对某些保存数据到模型中的算法比较有效,如KNN。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import joblib
# 加载数据
iris = load_iris()
X = iris.data
Y = iris.target
# 切割数据
test_size = 0.3
seed = 7
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=test_size,random_state=seed)
# 训练模型
model = LogisticRegression()
model.fit(X_train,Y_train)
# 保存模型
model_file = "./finalized_model.sav"
with open(model_file,"wb") as f:
# 序列化模型
joblib.dump(model,f)
# 加载模型
with open(model_file,"rb") as f:
# 反序列化模型
loaded_model = joblib.load(f)
result = loaded_model.score(X_test,Y_test)
result8、反馈跟踪
反馈跟踪的目的,是实现数据闭环。
9、案例
9.1 问题定义
-
导入数据集
import warnings warnings.filterwarnings("ignore") boston = load_oston() # 获取数据 data = pd.DataFrame(boston.data,columns=boston.feature_names) data_tmp = pd.Series(boston.target,name="MEDV") data = pd.concat([data,data_tmp],axis=1,join="outer") print("---------------------------------------------") # 查看数据维度 print("数据维度:",data.shape) print("---------------------------------------------") # 头5条数据 data.head()数据中包含14个特征和506条数据:
- CRIM:城镇人均犯罪率
- ZN:住宅用地所占比例
- INDUS:城镇中非住宅用地所占比例
- CHAS:CHAS虚拟变量,用于回归分析
- NOX:环保指数
- RM:每栋住宅的房间数
- AGE:1940年以前建成的自主单位的比例
- DIS:距离波士顿的就业中心的加权距离
- RAD:距离高速公路的便利指数
- TAX:每一万美元的不动产税率
- PRTATIO:城镇中的教师学生比例
- B:城镇中的黑人比例
- LSTAT:地区中有多少房东属于低收入人群
- MEDV:自住房屋房价中位数
9.2 特征工程
-
查看特征字段数据类型
data.dtypes -
查看描述性统计信息
data.describe().apply(lambda x:round(x,1)) -
查看pearson系数
data.corr(method="pearson").apply(lambda x:round(x,2))有些特征属性之间具有强关联关系(>0.7或<-0.7)
-
单一特征图表
-
直方图
data.hist(sharex=False,sharey=False,xlabelsize=1,ylabelsize=1,figsize=(10,8))
-
密度图
data.plot(kind="density",subplots=True,layout=(4,4),sharex=False,sharey=False,fontsize=1,figsize=(10,8))
-
箱线图
data.plot(kind="box",subplots=True,layout=(4,4),sharex=False,sharey=False,fontsize=8,figsize=(10,8))
-
-
多重数据图表
from pandas.plotting import scatter_matrix scatter_matrix(data,figsize=(15,15)) -
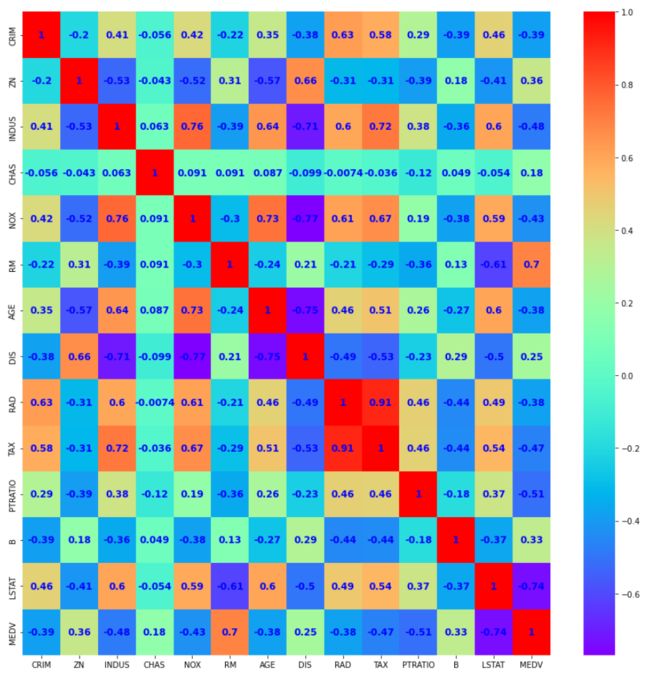
查看相关矩阵图
# 画法一: # import numpy as np # fig = plt.figure(figsize=(10,10)) # ax = fig.add_subplot(111) # cax = ax.matshow(data.corr(),vmin=1,vmax=1,interpolation="none") # fig.colorbar(cax) # ticks=np.arange(0,14,1) # ax.set_xticks(ticks) # ax.set_yticks(ticks) # ax.set_xticklabels(data.columns) # ax.set_yticklabels(data.columns) # 画法二: import seaborn as sns fig = plt.figure(figsize=(15,15)) ax = fig.add_subplot(111) # 绘制相关性系数热力图 sns.heatmap(data.corr(), annot=True, cmap="rainbow",ax=ax, annot_kws={ "size":12, "weight":"bold", "color":"blue" })有些属性之间是强相关的,可以在后续的处理中移除这些特征属性来提高算法的准确度。
-
分离评估数据集
选择80%数据作为训练数据,20%数据作为验证数据
from sklearn.model_selection import train_test_split # 分离数据集 X = data.iloc[:,0:13] Y = data.iloc[:,13] test_size = 0.2 seed = 7 X_train,X_test,Y_train,Y_test = train_test_split(X,Y, test_size=test_size, random_state=seed)
9.3 模型选择
9.3.1 初步评估算法-原始数据
-
使用原始数据集评估算法,形成算法的评估基准。
from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score # 3个线性算法 from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.linear_model import ElasticNet # 3个非线性算法 from sklearn.neighbors import KNeighborsRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.svm import SVR num_folds = 10 seed = 7 # 均方误差 scoring = "neg_mean_squared_error" models = {} models["LR"] = LinearRegression() models["LASSO"] = Lasso() models["EN"] = ElasticNet() models["KNN"] = KNeighborsRegressor() models["CART"] = DecisionTreeRegressor() models["SVM"] = SVR() results = [] for key in models: # 10折交叉验证 kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True) cv_result = cross_val_score(models[key], X_train, Y_train, cv=kfold, scoring=scoring) results.append(cv_result) print("%s : %f (%f)" % (key,cv_result.mean(),cv_result.std())) -
用箱线图来可视化算法结果
# 评估算法 fig = plt.figure() ax = fig.add_subplot(111) fig.suptitle("Algorithm Comparison") plt.boxplot(results) ax.set_xticklabels(models.keys()) plt.show()
9.3.2 二次评估算法-正态化数据
-
使用正态化后的数据,评估算法
正态化:“0”为中位数,“1”为标准差的数据。
对数据正态化时,为了防止数据泄露,采用Pipeline来正态化数据和对模型进行评估
from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler pipelines = {} pipelines["ScalerLR"] = Pipeline([("Scaler",StandardScaler()), ("LR",LinearRegression())]) pipelines["ScalerLASSO"] = Pipeline([("Scaler",StandardScaler()), ("LASSO",Lasso())]) pipelines["ScalerEN"] = Pipeline([("Scaler",StandardScaler()), ("EN",ElasticNet())]) pipelines["ScalerKNN"] = Pipeline([("Scaler",StandardScaler()), ("KNN",KNeighborsRegressor())]) pipelines["ScalerCART"] = Pipeline([("Scaler",StandardScaler()), ("CART",DecisionTreeRegressor)]) pipelines["ScalerSVM"] = Pipeline([("Scaler",StandardScaler()), ("SVM",SVR())]) results = list() for key in pipelines: kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True) cv_result = cross_val_score(pipelines[key], X_train, Y_train, cv=kfold, scoring=scoring) results.append(cv_result) print("%s : %f (%f)" % (key,cv_result.mean(),cv_result.std())) -
用箱线图来可视化算法结果
# 评估算法 fig = plt.figure() ax = fig.add_subplot(111) fig.suptitle("Algorithm Comparison") plt.boxplot(results) ax.set_xticklabels(models.keys()) plt.show()可以看到 KNN算法具有最优的MSE和比较紧凑的数据分布。
9.4 模型优化
9.4.1 算法调参
KNN算法的默认参数近邻个数(n_neighbors)为5。
# 针对 KNN,进行调参
from sklearn.model_selection import GridSearchCV
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {
"n_neighbors":[1,3,5,7,9,11,13,15,17,19,21]
}
model = KNeighborsRegressor()
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
grid = GridSearchCV(estimator=model,
param_grid=param_grid,
scoring=scoring,
cv=kfold)
grid_result = grid.fit(X=rescaledX,y=Y_train)
print("最优:%s 使用:%s" % (grid_result.best_score_,grid_result.best_params_))
cv_results = zip(grid_result.cv_results_["mean_test_score"],
grid_result.cv_results_["std_test_score"],
grid_result.cv_results_["params"])
for mean,std,param in cv_results:
print("%f (%f) with %r" % (mean,std,param))最优结果:KNN算法的近邻个数为1。
9.4.2 使用集成算法
-
使用正态化后的数据,评估算法
# 提升算法 AdaBoost(AB) 和 随机梯度上升(GBM) from sklearn.ensemble import AdaBoostRegressor from sklearn.ensemble import GradientBoostingRegressor # 袋装算法 随机森林(RF) 和 极端随机数(ET) from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import ExtraTreesRegressor # 将数据进行正态化后,进行算法拟合 ensembles = {} ensembles["ScaledAB"] = Pipeline([("Scaler",StandardScaler()), ("AB",AdaBoostRegressor())]) ensembles["ScaledAB-KNN"] = Pipeline([("Scaler",StandardScaler()), ("ABKNN",AdaBoostRegressor(base_estimator=KNeighborsRegressor(n_neighbors=1)))]) ensembles["ScaledAB-LR"] = Pipeline([("Scaler",StandardScaler()), ("ABLR",AdaBoostRegressor(base_estimator=LinearRegression()))]) ensembles["ScaledGBR"] = Pipeline([("Scaler",StandardScaler()), ("GBR",GradientBoostingRegressor())]) ensembles["ScaledRFR"] = Pipeline([("Scaler",StandardScaler()), ("RFR",RandomForestRegressor())]) ensembles["ScaledETR"] = Pipeline([("Scaler",StandardScaler()), ("ETR",ExtraTreesRegressor())]) results = [] for key in ensembles: kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True) cv_result = cross_val_score(ensembles[key],X_train,Y_train,cv=kfold,scoring=scoring) results.append(cv_result) print("%s : %f (%f)" % (key,cv_result.mean(),cv_result.std())) -
用箱线图来可视化算法结果
# 评估算法 fig = plt.figure(figsize=(10,8)) ax = fig.add_subplot(111) fig.suptitle("Algorithm Comparison") plt.boxplot(results) ax.set_xticklabels(ensembles.keys()) plt.show()可以发现 随机梯度上升算法(GBM)和 极端随机数算法(ET)具有较高的中位数。
9.4.3 集成算法调参
# 对GBM调参
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {
"n_estimators":[i for i in range(10,1000,100)]
}
model = GradientBoostingRegressor()
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
grid = GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv=kfold)
grid_result = grid.fit(X=rescaledX,y=Y_train)
print("GBM >>> 最优:%s 使用:%s" % (grid_result.best_score_,grid_result.best_params_))
# 对ETR调参
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = {
"n_estimators":[i for i in range(5,100,5)]
}
model = ExtraTreesRegressor()
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
grid = GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv=kfold)
grid_result = grid.fit(X=rescaledX,y=Y_train)
print("ETR >>> 最优:%s 使用:%s" % (grid_result.best_score_,grid_result.best_params_))ETR优于GBM。
9.5 确定最终模型
from sklearn.metrics import mean_squared_error
# 确定最终模型
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
etr = ExtraTreesRegressor(n_estimators=80)
etr.fit(X=rescaledX,y=Y_train)
rescaledY_test = scaler.transform(X_test)
predictions = etr.predict(rescaledY_test)
print("模型准确度:%s" % mean_squared_error(Y_test,predictions))![]()
参考
- 《机器学习 Python实践》 魏贞原 ISNB:978-7-121-33110-7
- 《https://www.cnblogs.com/nuochengze/p/15725751.html》