C语言调用MKL进行矩阵计算—特征值特征向量求解

C语言调用MKL进行矩阵计算—特征值特征向量求解

MKL的安装与配置

Intel数学核心函数库（MKL）是一套高度优化、线程安全的数学例程、函数，面向高性能的工程、科学与财务应用。英特尔 MKL 的集群版本包括 ScaLAPACK 与分布式内存快速傅立叶转换，并提供了线性代数 (BLAS、LAPACK 和Sparse Solver)、快速傅立叶转换、矢量数学 (Vector Math) 与随机号码生成器支持。所以用来做矩阵运算是最好不过啦。

MKL的具体的安装和配置可以参考
http://blog.csdn.net/caoenze/article/details/46699327
亲测可行，里面的示例代码也是好用的。

求解特征值特征向量函数—LAPACKE_dgeev

头函数为 #include “mkl.h”
先给出函数的定义
lapack_int LAPACKE_dgeev( int matrix_layout, char jobvl, char jobvr,lapack_int n, double* a, lapack_int lda, double* wr, double* wi, double* vl, lapack_int ldvl, double* vr,lapack_int ldvr );
参数解释：

matrix_layout 可选LAPACK_COL_MAJOR or LAPACK_ROW_MAJOR
jobvl N，表示不求左特征向量， V，表示要求
jobvr 同jobvl,是对右特征向量的选项（右特征向量为常用的特征向量）
n matrix的列数
a matrix
lda a矩阵的行数，lda>=max of(1,n)
wr 返回的特征值的实部
wi 返回的特征值的虚部
vl 左特征向量的存储空间
ldvl 左特征向量的行数
vr 右特征向量的存储空间
ldvr 右特征向量的行数
return 返回值为int info = 0, SUCCESS， -i, 第i个参数错误 +i, 表示执行错误

特别注意：特征值的实部和虚部是分为两个数组wr wi分别输出的，对应的特征向量的实部和虚部却是存在同一数组vl/vr里，所以提取时要注意。而且存储得很“节省”，具体方式如下面的例子。

#include 
#include 
#include "mkl.h"
#define n 4
int main()
{

    int matrix_order = LAPACK_COL_MAJOR;
    char jobvl = 'N';
    char jobvr = 'V';
    double A[n*n] = { 
         0.35,  0.09, -0.44,  0.25,
         0.45,  0.07, -0.33, -0.32,
        -0.14, -0.54, -0.03, -0.13,
        -0.17,  0.35,  0.17,  0.11};//4*4矩阵
    int lda = n;
    double wr[n] = {0};
    double wi[n] = {0};
    double vl[n*n];
    int ldvl = n;
    double vr[n*n];
    int ldvr = n;
    int info = LAPACKE_dgeev(matrix_order,jobvl,jobvr,n,A,lda,wr,wi,vl,ldvl,vr,ldvr);

    if(info==0){
        int i = 0;
        int j = 0;
        int flag = 0;//区分复特征值的顺序
        for(i=0;iprintf("eigenvalue %d:",i);
            printf("%.6g + %.6gi\t",wr[i],wi[i]);
            printf("\n");
            printf("right eigenvector: ");
            if(wi[i]==0)
            {
                    for(j=0;jprintf("%.6g\t",vr[i*n+j]);
                }
            }
            else if(flag==0)//如果该复特征值为这对复特征值的第一个则
            {
                flag=1;
                for(j=0;jprintf("%.6g + %.6gi\t",vr[i*n+j],vr[(i+1)*n+j]);
                }
            }
            else if(flag==1)//如果该复特征值为这对复特征值的第二个则
            {
                flag=0;
                for(j=0;jprintf("%.6g + %.6gi\t",vr[(i-1)*n+j],-vr[i*n+j]);
                }
            }
            printf("\n");
        }
        getchar();//必须要有这句
        printf("SUCCESS\n");
    }
    return 0;
}

给出输出结果：

上面的结果经验证是正确的
http://www.nag.co.uk/lapack-ex/examples/results/dgeev-ex.r
给出特征向量的监视结果方便大家分析：

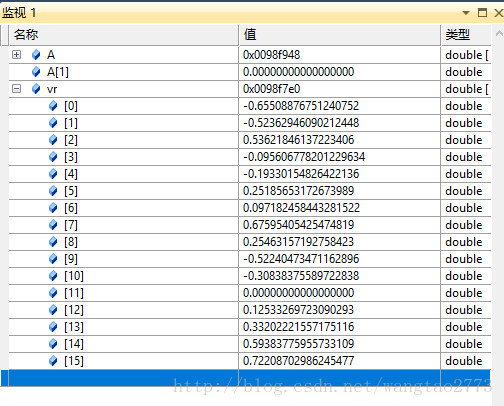
从输出结果和监视结果可以发现该函数的输出有一个问题就是特征值若为复数，则其虚部有单独一个数组来保存，而特征向量不是这样。可以注意eigenvector1、2这一对复特征值对应的复特征向量的实部都存在vr[4]—vr[7]中，虚部存在vr[8]—vr[11]中，虚部的正负有区分。查看官方文档，里面是这样说的：If the j-th eigenvalue is real, then u(j) = vl(:,j), the j-th column of vl. If the j-th and (j+1)-st eigenvalues form a complex conjugate pair, then u(j) = vl(:,j) + i*vl(:,j+1) and (j+1) = vl(:,j) - i*vl(:,j+1), where i = sqrt(-1).所以代码中设了flag来区分。

getchar();说明

代码段里的getchar();必须要有，我之前自己写的时候没有加这句，输出窗口就一直不显示，单步运行的时候又报了expression:_CtrlValidHeapPointer(pUserData)在网上查了半天说是内存释放和库链接的问题，导致思路跑偏，改了好久也没改好，后来突然醒悟加上getchar之后一切恢复，如果有人也遇到这样的报错尝试一下getchar吧。
C语言撂下太久了，平常写的代码也不多，一点小经验给大家分享一下。