综述：演化遗传学发展历史简介

本文主要翻译并精简自文章：Orr, H. The genetic theory of adaptation: a brief history. Nat Rev Genet 6, 119–127 (2005). https://doi.org/10.1038/nrg1523

名词解释

• 自然适应（Adaptation）：指群体向最适合当前环境的表型所进化的过程。
• 常设遗传变异（Standing Genetic Variation）：指在群体中已长期存在的变异，而非新出现的变异。

微突变理论（Micromutationism）

达尔文（Charles Darwin）在 1859 年的《物种起源》中提出：自然选择只能通过利用微小的连续变化来发挥作用；自然选择不能跳跃，它必须以最短和最慢的步子前进（natural selection can act only by taking advantage of slight successive variations; she can never take a leap, but must advance by the shortest and slowest steps）。

达尔文微突变理论的假设背景为：生物体只有通过许多微小的调整（变化），才能实现对环境的精确适应。

随着孟德尔遗传学派的兴起，达尔文的微突变理论受到挑战：生物体中存在能明显影响表型的突变，生物可以通过较大的调整来实现与环境匹配。但孟德尔理论无法解释数量性状的调控机制。

无穷小模型（Infinitesimal Model）

费舍尔（Ronald A. Fisher）在 1930 年弥合了两派观点的分歧，针对数量性状提出了 “无穷小模型” ：数量性状是由无数个突变综合影响的结果，各个突变对表型的影响相等且很小，效应是加性的，突变之间不存在上位性互作。无穷小模型为微突变理论提供了微观层面基础，并将理论的适用范围限定在了数量性状。

费舍尔构建了一个空间坐标系，每个坐标轴代表了一个生物体适应环境所需的性状，原点代表 当前环境下 生物体适应环境的 最佳表型，坐标值代表了生物体各表型距当前环境下最佳表型的偏离程度。当物种所处生存环境发生改变后，在新自然选择的压力下不断进化的情景，反映在空间坐标系中即为：物种的野生型原先处于空间原点的位置，但当生存环境改变后，野生型偏离了原点，在自然选择的压力下不断向原点前进。但由于突变是随机的，突变的效应或大或小，或好或坏，前进的方向与幅度依赖于每代随机突变中最优的突变，所以前进的过程具有随机性。

当我们只考虑 3 个性状时，可以绘制出下图（截取自参考文献）。图中第 $i$ 个球面距离球心的距离（半径 $r_i$），表示环境改变后第 $i$ 代群体的表型与最佳表型间的差异。图中红色折线中的向量 $v_i$ 表示群体第 $i-1$ 代到 $i$ 代过程中群体的进化方向及大小。整个红色折线表示了群体由野生型向新最佳表型不断进化的过程。

在上述模型中，可以将代表突变的向量分解为 指向球心 $v^{centre}$ 和 与球面向切 $v^{border}$ 两部分，若突变 $i$ 满足 $0<v_i^{centre}<2r$ ，则称突变 $i$ 为有益突变。可以发现，当 $|v|>2r$ 时，要满足 $v_{centre}<2r$ 就必须对 $v$ 和 $v^{centre}$ 之间的夹角 $\theta$ 进行限制。设 $v\ast cos\alpha =2r$，则当 $\alpha <\theta <90°$ 时，突变为有益突变。随着突变效应（$|v|$）的增加，$\theta$ 的取值范围被不断压缩，随机突变 i 是有益突变的概率不断降低。费舍尔根据上述数学模型，提出以下推论：

1. 当环境变化不大时，野生型与新环境下的最佳表型差异较小，所以突变是有害突变的概率随着突变效应的增加而升高。
2. 随着群体的不断进化，表型与最佳表型间的差异不断减小，所以突变是有害突变的概率随着半径的减小而升高。

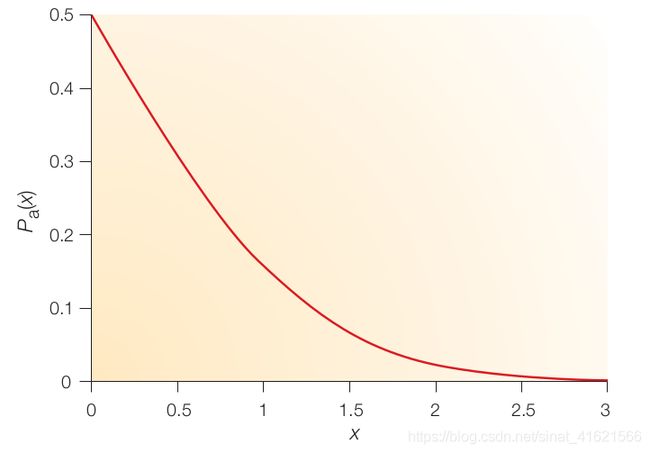
综上，除了环境剧烈变化的情况外，大效应突变是有益突变的概率极低，而小效应突变是有益突变的概率较高；并且随着群体的不断进化，小效应突变的优势越来越明显。突变效应大小（$x$）与有益突变概率（$P_a(x)$）之间的数学关系参见下图（摘自参考文献）：

无限小的突变有 50% 的机会是有利的；随着突变效应的增大，突变有益的概率会迅速下降。所以，费舍尔认为虽然在进化中可能会有效应较大的突变被保留，但这种突变的数量是极少的，保留下来的基本上都是小效应的突变，小效应突变是物种进化的基础。

序列进化模型（Sequence evolution）

随着对生命的认识逐渐深入到微观分子层面，人们开始尝试研究分子突变、表型变化与生物适应性之间的关系。无穷小模型中 “所有突变是等价的” 这一观点在分子层面产生了矛盾：不可能不同位点的突变是等价的，不可能位点突变成不同的碱基是等价的。梅纳德·史密斯（John Maynard Smith）在 1962 年提出了序列进化模型，阐述了突变在分子层面的特征和群体在不同适应性突变下如何进化成最佳表型的过程：

1. 与特定表型相关的序列长度是有限的。
2. 由于生物体 DNA 突变率低，梅纳德·史密斯认为每代个体内的突变不存在同一个位点的反复突变，也不存在多个位点同时突变，即每代个体相比于父代至多突变一个位点。设序列长度为 $L$，则每代群体中至多存在 $3L$ 种不同的序列，而非 $4^L-1$ 种。
3. 群体向最佳表型进化的过程也是序列从野生型 逐步 （$i$ 代的最佳序列相比 $i-1$ 代的最佳序列，只有一个位点的差异）突变成最佳序列的过程。梅纳德·史密斯将此过程称为 适应性行走（adaptive walks）。

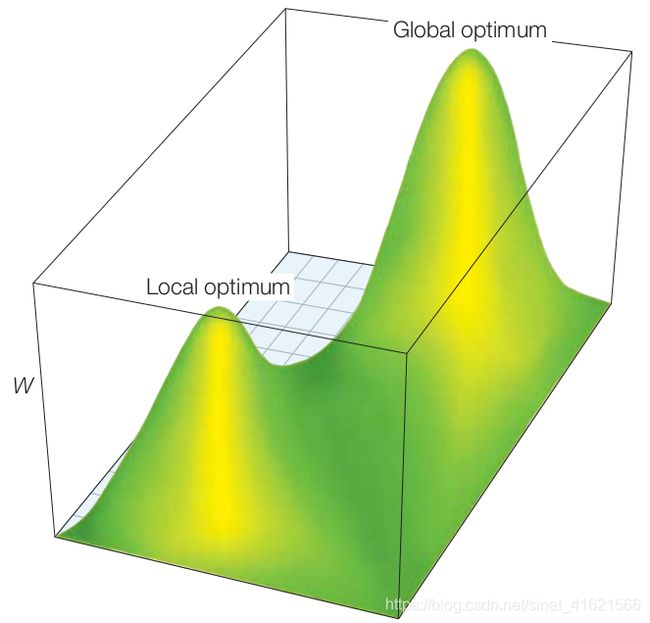
按照序列进化模型，如果将基因中所有可能的 DNA 序列想象成一个平面上的所有点，彼此略有不同的序列在平面上彼此相邻，而差异较大的序列则相距较远；每个序列的适应度表示为该点在平面上方的高度；由此可以绘制出一幅包含山丘和山谷的三维图片，如下图所示（摘自参考文献），山丘的崎岖程度反映了各突变之间的适应性差异。自然环境的变化，让原先的山丘变为山谷，野生型向最佳表型进化的过程，即 适应性行走为从山谷向山峰攀登的过程。学者们将下图称为 fitness landscape 或者 adaptive landscape。由于突变方向的随机性，适应性行走更大的概率是攀登上一个局部最优解的山峰，而非全局最优解的山峰。

吉莱斯皮花费了大量时间来研究 adaptive landscape 的特点，他发现：

1. 随着序列的适应度在不断增加，有益突变的数量指数性减少。
2. 适应性行走的平均步数较少。群体一般经过 2-5 次进化即可达到局部最优解。

极值理论（Extreme Value Theory，EVT）

费舍尔的无穷小模型计算突变适应性（fitness）的分布，需要度量野生型与最佳表型之间的距离，这在诸多研究中难以实现。序列进化模型也没有计算突变适应性的分布。为此，吉莱斯皮（John H. Gillespie）在 1984 年将极值理论引入到了分子进化领域。Gillespie 使用极值理论的背景是：

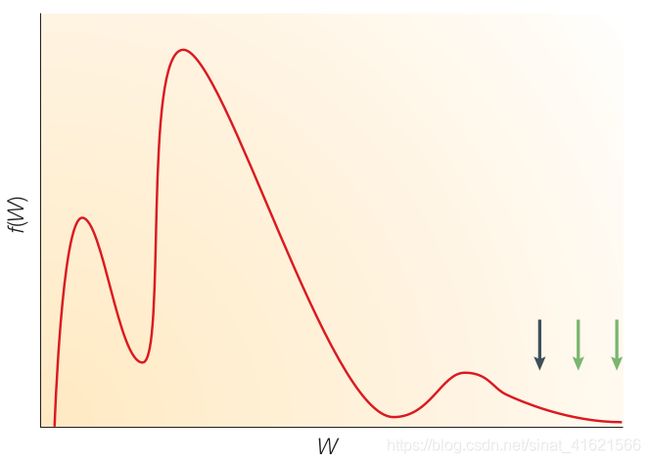
1. 在非剧烈环境下，野生型（$v^w$，下图 墨绿色 箭头）与最适表型差异较小，在突变适应性的分布（$D$）中 野生型处在分布的右尾端。
2. 适应性落在野生型右端的突变称为有益突变（$v^b$，下图 绿色 箭头），所以有益突变处在整个突变分布的更极端区间，可以近似认为 有益突变的适应性是最大适应性。
3. 如果将一个群体中的突变适应性的集合视为是在突变适应性分布中的一次抽样（$S(D{)}_i$），则有益突变可以近似视为本次抽样中适应性的最大值（$v_i^b=max(S(D{)}_i)$）。如果有 $N$ 个群体在相同环境下独立进化，则各群体中有益突变所组成的集合（$V^b$，$V^b=\{v_1^b,v_2^b,...,v_i^b,...,v_N^b\}$）的分布，即为对突变适应性分布进行 $N$ 次独立抽样中最大值的分布（$V^b=\{max(S(D{)}_1),max(S(D{)}_2),...,max(S(D{)}_i),...,max(S(D{)}_N)\}$）。

极值理论表明，当我们仅关注每次独立抽样中最大值的分布（$V^b$）时，其分布（$V^b$）特征与原分布（$D$）无关。所以吉莱斯皮利用极值理论可以直接研究有益突变的分布特征（$V^b$），而无需知晓突变适应性整体的分布特征（$D$）。

大部分常见分布 —— 如正态（normal）、对数正态（lognormal）、伽马（gamma）、指数（exponential）、威布尔（Weibull）、逻辑（logistic）等 —— 的极值分布都符合耿贝尔分布（Gumbel distribution），所以吉莱斯皮假设认为有益突变的分布也符合耿贝尔分布。极值理论不仅描述了来自父分布的最大值的分布，还描述了最大值与次大值、第三大值、第四大值分布之间的规律 —— 指数函数，即极值理论认为，有益突变的适应度成指数下降趋势。

如下图所示（摘自参考文献），横坐标表示突变的适应性（$W$），纵坐标表示突变发生的频率（$f(W)$），红色曲线表示突变适应性整体的分布特征（$D$），墨绿色箭头表示野生型的适应性，绿色箭头表示有益突变的适应性，墨绿色箭头左侧的红色曲线为随意绘制。

总结

上面介绍了随人们对生命及进化认识的不断加深而提出的 3 种理论。新理论并不是对旧理论的全面否定，而是对其部分内容进行更新并补充上新的理论。但由于所有理论的提出都是基于一些重要且理想化的假设，并且目前对理论验证的实验还不够充分。所以理论的合理性仍有待进一步证明，更多是一种定性的理解。总的来说，现在观察到的情况是：

1. 小效应的有益突变多于大效应（QTL 研究揭示了比大效应更多的小效应替代）；
2. 微生物研究表明，早期替代比后期替代具有更大的适应度效应（即存在收益递减模式）；