融合正余弦和柯西变异的麻雀搜索算法-附代码

融合正余弦和柯西变异的麻雀搜索算法

摘要：针对麻雀搜索算法（SSA）在寻优后期出现能力不足、种群多样性损失、易落进局部极值现象，造成SSA算法收敛速度慢、探索能力不足等问题，提出了融合正余弦和柯西变异的麻雀搜索算法（SCSSA）。首先借助折射反向学习机制初始化种群，增加物种多样性；然后在发现者位置更新中引入正余弦策略以及非线性递减搜索因子和权重因子协调算法的全局和局部寻优能力；最后在跟随者位置中引入柯西变异对最优解进行扰动更新，提高算法获取全局最优解能力。

1.麻雀搜索算法

基础麻雀算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/108830958

2.改进麻雀算法

2.1 折射反向学习策略

针对 SSA 算法在寻优后期出现群体多样 性损失, 造成落人局部极值的几率升高, 引 发收敛精度不足问题，本文采用一种折射反 向学习机制对麻隹种群初始化。反向学习是 Tizhoosh 提出的一种优化策略 ${}^{[9]}$, 基本思想是 通过计算当前解的反向解来扩大搜索范围, 借此找出给定问题更好的备选解。文献[1011]将智能算法与反向学习的结合, 均能有效 提高算法求解精度。同时反向学习仍存在一 定的不足, 在寻优早期引进反向学习能加强 算法的收敛性能, 但在后期易使算法陷人早 熟收敛。因此在反向学习策略中引进一种折 射原理 ${}^{[12]}$ 以降低算法在搜索后期陷人早熟收 敛的几率。折射反向学习原理如图 1所示。

其中, $x$ 轴上面解的寻优范围为 $[,u],y$ 轴为法线, $\alpha 、\beta$ 分别表示人射角、折射角, $h$ 和 $h^{\ast }$ 分别为入射、折射光线所对应的长度, $O$ 为寻优范围 $[,u]$ 的中点。根据数学中线几何 关系, 得到如下:
$$\begin{array}{rl}& \sin \alpha =((l+u)/2-x)/h\\ & \sin \beta =\left(x^{\ast }-(l+u)/2\right)/h^{\ast }\end{array}\text{\hspace{1em}(4)}$$
根据折射率定义 $n=\sin \alpha /\sin \beta$, 得到折 射率 $n$ 公式为:
$$n=\frac{h^{\ast }((l+u)/2-x)}{h\left(x^{\ast }-(l+u)/2\right)}\text{ (5) }$$
令缩放因子 $k=h/h^{\ast }$, 带人式（5）得到 变形公式为:
$$x^{\ast }=\frac{l+u}{2}+\frac{l+u}{2kn}-\frac{x}{kn}\text{ (6) }$$
当 $n=1$ 且 $k=1$ 时, 式 ( 6 ) 可转为反 向学习公式 ${}^{[11]}$ :
$$x^{\ast }=l+u-x\text{ (7) }$$
式 (6) 推广到麻雀算法高维空间时, 令 $n=1$ 可得到如下:
$$x_{i,j}^{\ast }=\frac{l_j+u_j}{2}+\frac{l_j+u_j}{2k}-\frac{x_{i,j}}{k}\text{ ( 8) }$$
式中: $x_{i,j}$ 为种群中第 $i$ 只麻雀在 $j$ 维位置 $(i=1,2,\dots ,D;j=1,2,\dots ,N),D$ 为种群数， $N$ 为维度; $x_{i,j}^{\ast }$ 为 $x_{i,j}$ 的折射反向位置; $l_j$ 、
$u_j$ 分别为搜索空间第 $j$ 维的最小值和最大值。

算法 1 初始化种群算法
（1）在寻优范围中随机初始化 $N$ 个麻雀 位置 $x_{i,j}$ 作为初始种群位置;
（2）根据式（8）生成折射反向种群 $x_{i,j}^{\ast }$;
(3) 合并初始种群和折射反向种群, 根 据适应度值的升降进行排序, 选取适应度值 前 $N$ 个麻雀个体作为初始种群。

2.2 正余弦策略

在麻雀捕食过程中, 食物源位置非常重 要作用, 影响整个麻雀种群前进方向。但考 虑到食物来源可能不同, 位置也不尽相同, 当发现者搜寻的食物位于局部最优时，大量 的跟随者会涌人到该位置，此时发现者与整 个群体停滞不前, 造成种群位置多样性出现 损失, 进而增加陷人局部极值的可能性。针 对该现象，本文在麻雀搜索算法发现者的位 置. 更新中引进正余弦算法 ( SineCosineAlgorithm,SCA ) ${}^{[13]}$ ，通过利用正余弦 模型震荡变化特性对发现者位置进行作用， 维持发现者个体多样性, 进而提高 $\mathrm{SSA}$ 的全 局搜索能力。 $\mathrm{SCA}$ 的中心思想是根据正余弦 模型的振荡变化对整体和局部寻优, 获取整 体最优值。
针对基本的正余弦算法的步长搜索因子 $r_1=a-at/$ Iter ${}_{\max }(a$ 为常数, $t$ 为迭代次数, 本文设置 $a=1$ )呈线性递减趋势, 不利于进 一步平衡 SSA 的全局搜索和局部开发能力,受文献[14]启发，对步长搜索因子进行改进，新的非线性递减搜索因子如式（9），在前期权重较大，递减速度慢，利于提高全局寻优能力，在权重因子较小时，增强算法在局部开发的优势，加快获取最优解的速度。
$$r_1^{\prime }=a\times {\left(1-{\left(\frac{t}{{\text{ Iter }}_{\max }}\right)}^{\eta }\right)}^{1/\eta }(9)$$
式中: $\eta$ 为调节系数, $\eta ⩾1;a=1$ 。
考虑 $\mathrm{SSA}$ 算法在整个抻索过程中, 种群 个体位真更新常受到当前位置影响。因此弓 进式（10）非线性权重因子心用于调整种群 个体位置更新对此时个体信自的依赖度。在 寻优前期, 较小的心降低了寻优个体位置更 新对当前解位置影吅, 提升了算法全居奇优 个体位真更新的高度依赖性, 加快了算法的 收敛速度, 变化曲线如图 2 所示。则得到新 的发现者位置更新公式如式 ( 10 ):
$$w=\frac{e^{\frac{t}{1t{e}_{\max }}}-1}{e-1}(10)$$

$$X_{i,j}^{t+1}=\{\begin{array}{l}\omega \cdot X_{i,j}^t+r_1{}^{\prime }\cdot \sin \left(r_2\right)\cdot \left|r_3\cdot X_{\text{best }}-X_{i,j}^t\right|R_2<ST\\ \omega \cdot X_{i,j}^t+r_1^{\prime }\cdot \cos \left(r_2\right)\cdot \left|r_3\cdot X_{\text{best }}-X_{i,j}^t\right|R_2⩾ST\end{array}\text{\hspace{1em}(11)}$$

式中: $r_2\in [0,2\pi ]$ 的随机数, 决定麻雀的移动距离 ; $r_3\in [0,2\pi ]$ 的随机数, 控制最优个 体对麻雀后一位置的影响。

2.3 柯西变异策略

在觅食过程中, 跟随者经常围绕最好的 发现者周围进行觅食, 其间也有可能发生食 物的争夺, 使其自已变成发现者, 为避免算 法陷人局部最优, 在跟随者更新公式中引人 柯西变异策略, 提升全局寻优能力。新的跟 随者位置更新如下：
$X_{i,j}^{t+1}=X_{\text{best }}(t)+\mathrm{cauchy}(0,1)\oplus X_{\text{best }}(t)$ ( 12 )
式中: $\mathrm{cauchy}(0,1)$ 为标准柯西分布函数;
$\oplus$表示相乘含义。
以原点为中心的一维柯西变异函数如下: $f(x)=\frac{1}{\pi }\left(\frac{1}{x^2+1}\right),-\infty <x<\infty$ ( 13$)$ 柯西分布与标准的正态分布相似, 为连续的 概率分布, 在原点处值较小, 两端较为扁长, 逼近零速率较慢, 因而相比于正态分布能产 生更大的扰动。因此, 利用柯西变异对麻﨎 位置更新中的个体进行扰动, 从而扩大麻雀 算法的搜索规模, 进而提升算法跳出局部最 优能力。

SCSSA 算法流程

步骤 1 设置种群大小 $N$, 最大迭代次数 Iter $r_{\max }$, 发现者比例 $PD$, 侦察者比例 $SD$, 警戒阈值 $R_2$, 安全阈值 $ST$ 等;

步骤 2 执行算法 1 对麻雀种群初始化;
步骤 3 计算每只麻﨎的适应度值并排序， 确定当前最优、最差适应度个体;
步骤 4 根据式（11）对发现者位置更新;
步骤 5 根据式 ( 12) 对跟随者位置更新;
步骤 6 根据式（3）对警戒者位置更新;
步骤 7 判断当前迭代次数是否达到结束条件, 若满足, 则进行下一步, 否则跳转步骤 3;
步骤 8 程序结束, 输出最优适应度值和最佳位置。

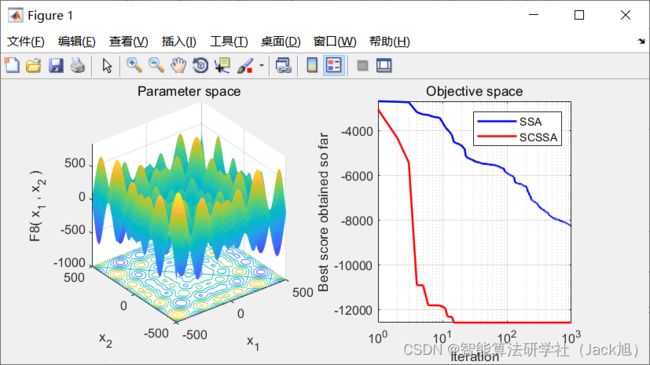
3.实验结果

4.参考文献

[1]李爱莲,全凌翔,崔桂梅,解韶峰.融合正余弦和柯西变异的麻雀搜索算法[J/OL].计算机工程与应用:1-11[2021-09-09].http://kns.cnki.net/kcms/detail/11.2127.TP.20210806.0937.008.html.

5.Matlab代码

6.python代码