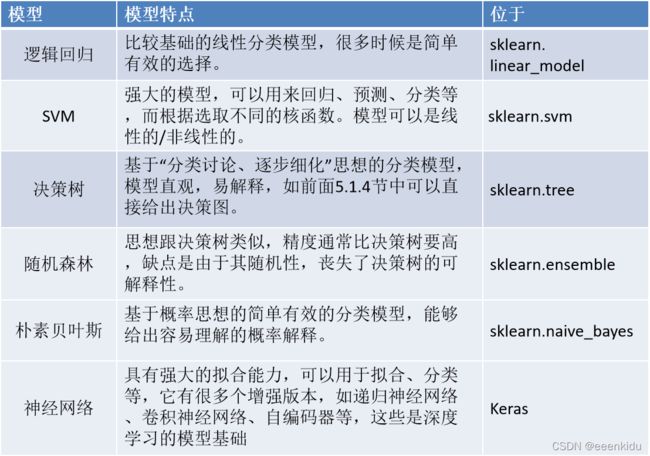
挖掘建模②—分类与预测（python实现简单线性关系 多项式拟合/回归）

Python介绍、 Unix & Linux & Window & Mac 平台安装更新 Python3 及VSCode下Python环境配置配置
python基础知识及数据分析工具安装及简单使用(Numpy/Scipy/Matplotlib/Pandas/StatsModels/Scikit-Learn/Keras/Gensim))
数据探索（数据清洗）①——数据质量分析（对数据中的缺失值、异常值和一致性进行分析）
数据探索（数据清洗）②—Python对数据中的缺失值、异常值和一致性进行处理
数据探索（数据集成、数据变换、数据规约）③—Python对数据规范化、数据离散化、属性构造、主成分分析 降维
数据探索（数据特征分析）④—Python分布分析、对比分析、统计量分析、期性分析、贡献度分析、相关性分析
挖掘建模①—分类与预测
挖掘建模②—Python实现预测
挖掘建模③—聚类分析(包括相关性分析、雷达图等)及python实现
挖掘建模④—关联规则及Apriori算法案例与python实现
挖掘建模⑤—因子分析与python实现

Python实现分类与预测

Logistic回归模型建模

体重与体重指数的简单线性关系

import pandas as pd  # 导入数据分析库Pandas
import matplotlib.pyplot as plt  # 导入图像库
from sklearn.linear_model import LinearRegression, Perceptron
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
data = pd.read_csv(f'tmp/sport.csv')
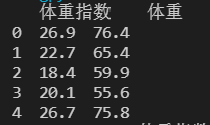
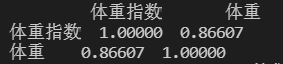
print(data[["体重指数", "体重"]].head())
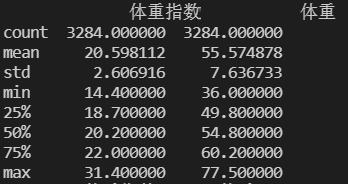
## 体重与体重指数的描述性分析
print(data[["体重指数", "体重"]].describe())

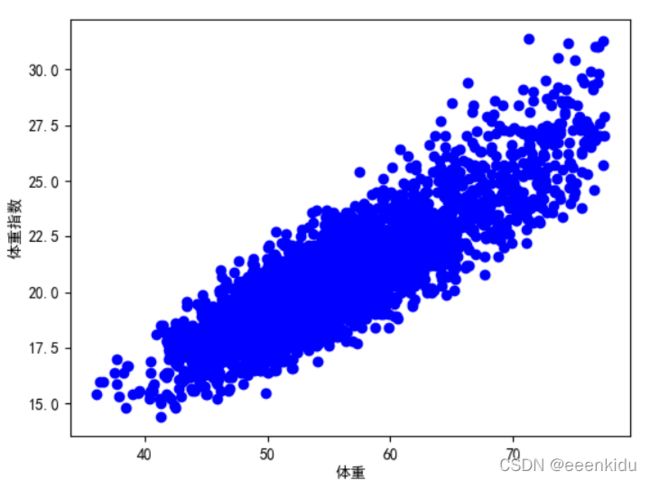
# 绘制散点图
plt.scatter(data[["体重"]], data[["体重指数"]], color='b', label="体重与体重指数")
# 添加图的标签（x轴，y轴）
plt.xlabel("体重")
plt.ylabel("体重指数")
plt.show()

print(data[["体重指数", "体重"]].corr())

# 将原数据集拆分训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(
    data[["体重"]], data[["体重指数"]], train_size=.8)
# X_train为训练数据标签,X_test为测试数据标签,exam_X为样本特征,exam_y为样本标签，train_size 训练数据占比
print('{:*^60}'.format("训练集和测试集的创建"))
print("原始数据特征:", data[["体重"]].shape,
      ",训练数据特征:", X_train.shape,
      ",测试数据特征:", X_test.shape)
print("原始数据标签:", data[["体重指数"]].shape,
         ",训练数据标签:", Y_train.shape,
         ",测试数据标签:", Y_test.shape)

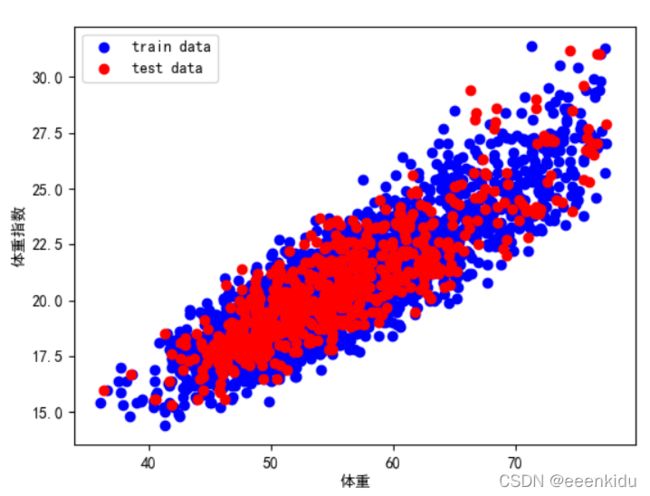
# 散点图
plt.scatter(X_train, Y_train, color="blue", label="train data")
plt.scatter(X_test, Y_test, color="red", label="test data")

# 添加图标标签
plt.legend(loc=2)
plt.xlabel("体重")
plt.ylabel("体重指数")
# 显示图像
plt.show()

model = LinearRegression()
# 对于模型错误我们需要把我们的训练集进行reshape操作来达到函数所需要的要求

# reshape如果行数=-1的话可以使我们的数组所改的列数自动按照数组的大小形成新的数组
# 因为model需要二维的数组来进行拟合但是这里只有一个特征所以需要reshape来转换为二维数组
X_train = X_train.values.reshape(-1, 1)
X_test = X_test.values.reshape(-1, 1)
model.fit(X_train, Y_train)
a = model.intercept_  # 截距
b = model.coef_  # 回归系数
print('{:*^60}'.format("获得最佳拟合线"))
print("最佳拟合线:截距", a, ",回归系数：", b)

# 训练数据的预测值
y_train_pred = model.predict(X_train)
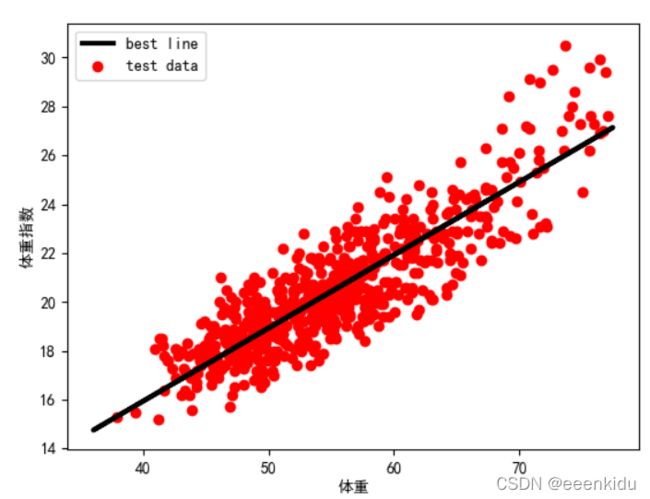
# 绘制最佳拟合线：标签用的是训练数据的预测值y_train_pred
plt.plot(X_train, y_train_pred, color='black',
         linewidth=3, label="best line")

# 测试数据散点图
plt.scatter(X_test, Y_test, color='red', label="test data")

# 添加图标标签
plt.legend(loc=2)
plt.xlabel("体重")
plt.ylabel("体重指数")
# 显示图像
plt.show()

score = model.score(X_test, Y_test)
print('{:*^60}'.format("决定系数R平方"))
print(score)

多项式拟合/回归

对体测成绩进行预测，首先对成绩进行相关性分析，选择了相关性较高的几项进行多项式拟合，最终选择"50米跑成绩", “一分钟仰卧成绩”, “立定跳远成绩”, “800米成绩” 对总分进行多项式拟合。

读取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Perceptron
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
data = pd.read_csv(f'tmp/sport.csv')
data=data[["体重指数成绩","一分钟仰卧成绩","坐位体前屈成绩","肺活量成绩","50米跑成绩","立定跳远成绩","800米成绩","总分"]]

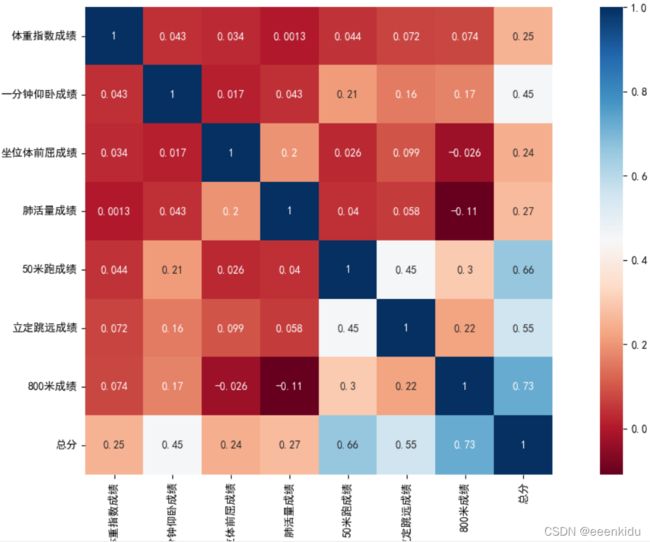
相关性分析

# 相关性分析
def plotcor(data):
    ylabels = data.columns.values.tolist()
    df = pd.DataFrame(data)
    dfData = df.corr()  # 相似度由皮尔逊相关系数度量
    # 皮尔逊相关系数——Pearson correlation coefficient，用于度量两个变量之间的相关性，其值介于-1与1之间，值越大则说明相关性越强。
    '''
    0.8-1.0     极强相关
    0.6-0.8     强相关
    0.4-0.6     中等程度相关
    0.2-0.4     弱相关
    0.0-0.2     极弱相关或无相关
    '''
    plt.subplots(figsize=(15, 10))  # 设置画面大小
    sns.heatmap(dfData, annot=True, vmax=1, square=True,
                yticklabels=ylabels, xticklabels=ylabels, cmap="RdBu")
    plt.show()
    
plotcor(data)

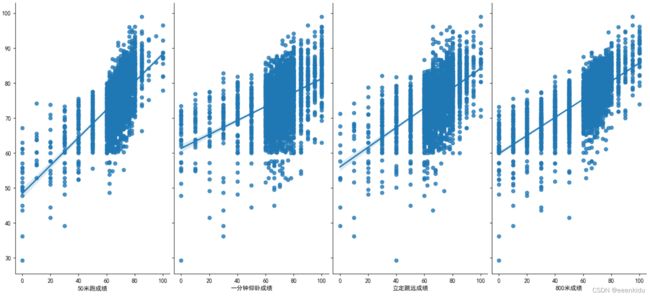
不同的因素对标签值的影响

def plotPair(data, targetstr, eigs):
    # 通过加入一个参数kind='reg'，seaborn可以添加一条最佳拟合直线和95%的置信带。
    sns.pairplot(data, x_vars=eigs, y_vars=targetstr,
                 size=7, aspect=0.8, kind='reg')
    plt.show()
plotPair(data, targetstr, eigs)

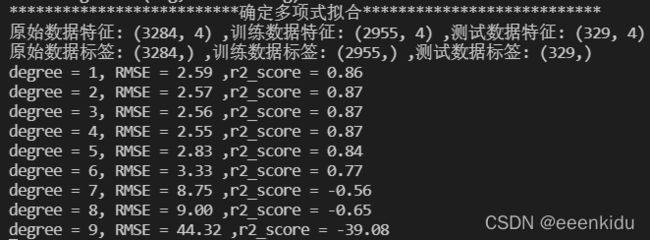
确定多项式回归的阶数

def selectDegree(data, targetstr, eigs, testsize):  # 确定多项式拟合/回归的阶数
    print('{:*^60}'.format("确定多项式拟合"))
    target = data[targetstr]
    data_complete_ = data.loc[:, eigs]
    x_train, x_test, y_train, y_test = train_test_split(
        data_complete_, target, test_size=testsize)
    print("原始数据特征:", data.loc[:, eigs].shape,
          ",训练数据特征:", x_train.shape,
          ",测试数据特征:", x_test.shape)

    print("原始数据标签:", data[targetstr].shape,
          ",训练数据标签:", y_train.shape,
          ",测试数据标签:", y_test.shape)

    rmses = []
    degrees = np.arange(1, 10)
    min_rmse, min_deg, score = 1e10, 0, 0

    for deg in degrees:
        # 生成多项式特征集(如根据degree=3 ,生成 [[x,x**2,x**3]] )
        poly = PolynomialFeatures(degree=deg, include_bias=False)
        x_train_poly = poly.fit_transform(x_train)

        # 多项式拟合
        poly_reg = LinearRegression()
        poly_reg.fit(x_train_poly, y_train)

        # 测试集比较
        x_test_poly = poly.fit_transform(x_test)
        y_test_pred = poly_reg.predict(x_test_poly)

        # mean_squared_error(y_true, y_pred) #均方误差回归损失,越小越好。
        poly_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred))
        rmses.append(poly_rmse)
        # r2 范围[0，1]，R2越接近1拟合越好。
        r2score = r2_score(y_test, y_test_pred)

        # degree交叉验证
        if min_rmse > poly_rmse:
            min_rmse = poly_rmse
            min_deg = deg
            score = r2score
        print('degree = %s, RMSE = %.2f ,r2_score = %.2f' %
              (deg, poly_rmse, r2score))

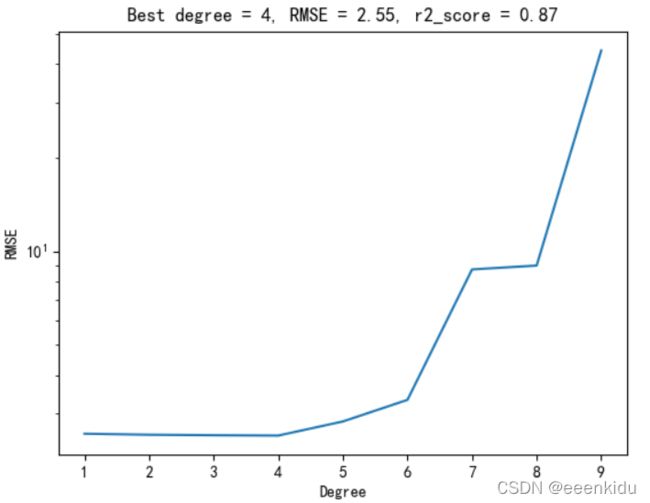
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(degrees, rmses)
    ax.set_yscale('log')
    ax.set_xlabel('Degree')
    ax.set_ylabel('RMSE')
    ax.set_title('Best degree = %s, RMSE = %.2f, r2_score = %.2f' %
                 (min_deg, min_rmse, score))
    plt.show()
    return min_deg


male_deg = selectDegree(data, targetstr, eigs, 0.1)

构建多阶多项式回归模型

def buildModel(data, deg, targetstr, eigs, testsize):
    target = data[targetstr]
    data_complete_ = data.loc[:, eigs]
    x_train, x_test, y_train, y_test = train_test_split(
        data_complete_, target, test_size=testsize)
    # 多项式拟合
    poly_reg = PolynomialFeatures(degree=deg)
    x_train_poly = poly_reg.fit_transform(x_train)
    model = LinearRegression()
    model.fit(x_train_poly, y_train)
    a = model.intercept_  # 截距
    b = model.coef_  # 回归系数
    print('{:*^60}'.format("多项式拟合"))
    print("最佳拟合线:截距", a, ",回归系数：", b)

    # 对线性回归进行预测  # 测试集比较
    x_test_poly = poly_reg.fit_transform(x_test)
    y_test_pred = model.predict(x_test_poly)
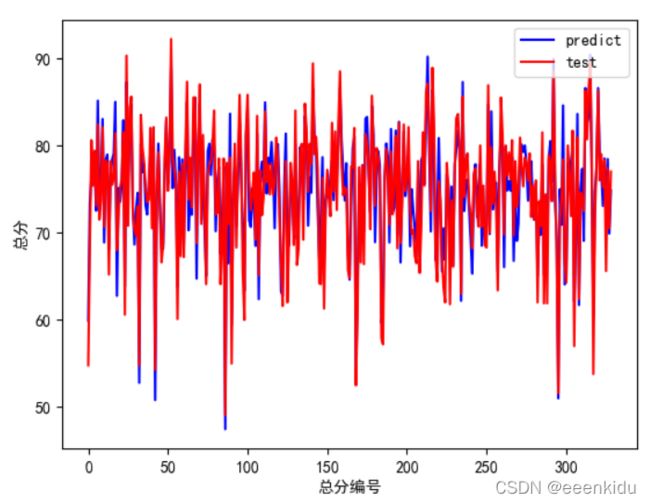
    # 预测集与源数据集的对比 绘制ROC曲线
    plotROC(y_test_pred, y_test, targetstr)
    score = model.score(x_test_poly, y_test)
    # r2 范围[0，1]，R2越接近1拟合越好。r2该数学模型对真实数据的解释度，为百分数。
    print('{:*^60}'.format("决定系数R平方"))
    print("score:", score)
    # mean_squared_error(y_true, y_pred) #均方误差回归损失,越小越好。估计量与被估计量之间差异程度的一种度量
    mse = np.sqrt(mean_squared_error(y_test, y_test_pred))
    print('{:*^60}'.format("均方误差回归损失"))
    print(mse)
def plotROC(y_test_pred, y_test, targetstr):
    plt.figure()
    plt.plot(range(len(y_test_pred)), y_test_pred, 'b', label="predict")
    plt.plot(range(len(y_test_pred)), y_test, 'r', label="test")
    plt.legend(loc="upper right")  # 显示图中的标签
    plt.xlabel(targetstr+"编号")
    plt.ylabel(targetstr)
    plt.show()

buildModel(data, male_deg, targetstr, eigs, 0.1)