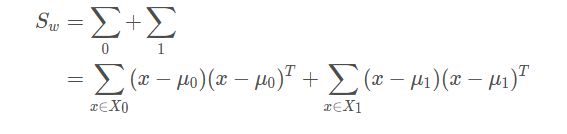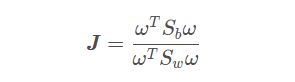线性判别准则(LDA)与线性分类算法(SVM))

一、线性判别分析简介

• 线性判别分析（Linear Discriminant Analysis，简称LDA）是一种经典的有监督数据降维方法。
• LDA的主要思想是将一个高维空间中的数据投影到一个较低维的空间中，且投影后要保证各个类别的类内方差小而类间均值差别大，这意味着同一类的高维数据投影到低维空间后相同类别的聚在一起，而不同类别之间相距较远。
  
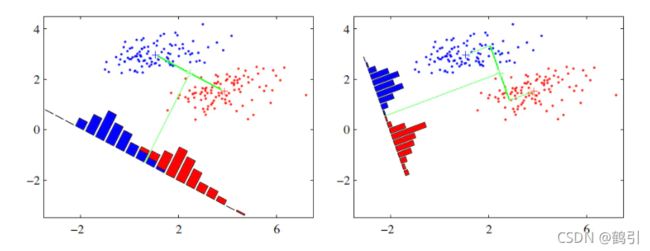
• 线性判别分析思想：给定训练样本集，设法将样例投影到一条直线上。使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远；在对新样本进行分类时，将其投影到该直线上，再根据投影点的位置来确定新样本的类别。

二、线性判别分析原理

假设现有数据集 $D=(x1,y1),(x1,y1),...,(xm,ym)$，其中任意样本xi为n维向量。定义Nj为第j类样本的个数，Xj为第j类样本的集合，而μj为第j类样本的均值向量，$\Sigma j(j=0,1)$为第j类样本的"方差"。

1. 类内散度矩阵

类内散度矩阵用来判断同类样例的投影点之间的距离。

2. 类间散度矩阵

类间散度矩阵用来判断异类样例的投影点之间的距离。

3. 广义瑞利商

广义瑞利商就是$LDA$欲最大化的目标。

三、Sklearn库实现线性判别分析

1. 采用随机数据集，导入包

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as lda#导入LDA算法
from sklearn.datasets._samples_generator import make_classification #导入分类生成器
import matplotlib.pyplot as plt #导入画图用的工具
import numpy as np
import pandas as pd

2. 产生随机数据

x,y=make_classification(n_samples=200,n_features=2,n_redundant=0,n_classes=2,n_informative=1,n_clusters_per_class=1,class_sep=0.5,random_state=100)
"""
n_features :特征个数= n_informative（） + n_redundant + n_repeated
n_informative：多信息特征的个数
n_redundant：冗余信息，informative特征的随机线性组合
n_repeated ：重复信息，随机提取n_informative和n_redundant 特征
n_classes：分类类别
n_clusters_per_class ：某一个类别是由几个cluster构成的

"""
plt.scatter(x[:,0],x[:,1], marker='o', c=y)
plt.show()
x_train=x[:60, :60]
y_train=y[:60]
x_test=x[40:, :]
y_test=y[40:]

3. 将数据集分为训练集和测试集，训练完之后利用测试集获得准确率

#分为训练集和测试集，进行模型训练并测试
x_train=x[:150, :150]
y_train=y[:150]
x_test=x[50:, :]
y_test=y[50:]
lda_test=lda()
lda_test.fit(x_train,y_train)
predict_y=lda_test.predict(x_test)#获取预测的结果
count=0
for i in range(len(predict_y)):
    if predict_y[i]==y_test[i]:
        count+=1
print("预测准确个数为"+str(count))
print("准确率为"+str(count/len(predict_y)))

四、SVM

1. 简介

1. SVM（支持向量机）主要用于分类问题，主要的应用场景有字符识别、面部识别、行人检测、文本分类等领域。
2. 通常SVM用于二元分类问题，对于多元分类通常将其分解为多个二元分类问题，再进行分类。

2. 距离衡量标准

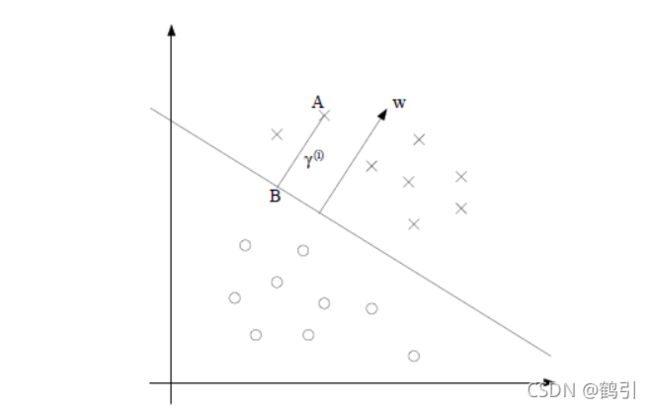
SVM的中心思想，即，使距离分隔平面最近的点的距离最大。
通常采用几何间隔作为距离度量的方式。

五、SVM数据集进行可视化分类

月亮数据集

1. 线性SVM

1. 导入包

# 导入月亮数据集和svm方法
#这是线性svm
from sklearn import datasets #导入数据集
from sklearn.svm import LinearSVC #导入线性svm
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import StandardScaler

2. 获取响应的月亮数据集
   
   • 月亮数据集是很圆滑的两个弧线，这里设置random_state，使数据没那么有规律
3. 进行标准化并进行数据训练

scaler=StandardScaler()# 标准化
scaler.fit(data_x)#计算训练数据的均值和方差
data_x=scaler.transform(data_x) #再用scaler中的均值和方差来转换X，使X标准化
liner_svc=LinearSVC(C=1e9,max_iter=100000)#线性svm分类器,iter是迭达次数，c值决定的是容错，c越大，容错越小
liner_svc.fit(data_x,data_y)

4. 绘制边界函数，进行后续可视化分类

# 边界绘制函数
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))
    # meshgrid函数是从坐标向量中返回坐标矩阵
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new)#获取预测值
    zz=y_predict.reshape(x0.shape)
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,cmap=custom_cmap)

6. 画图，输出参数已经截距权重

#画图并显示参数和截距
plot_decision_boundary(liner_svc,axis=[-3,3,-3,3])
plt.scatter(data_x[data_y==0,0],data_x[data_y==0,1],color='red')
plt.scatter(data_x[data_y==1,0],data_x[data_y==1,1],color='blue')
plt.show()
print('参数权重')
print(liner_svc.coef_)
print('模型截距')
print(liner_svc.intercept_)

这种情况下线性svm效果并不好

2. 多项式核

1. 导入所需的包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

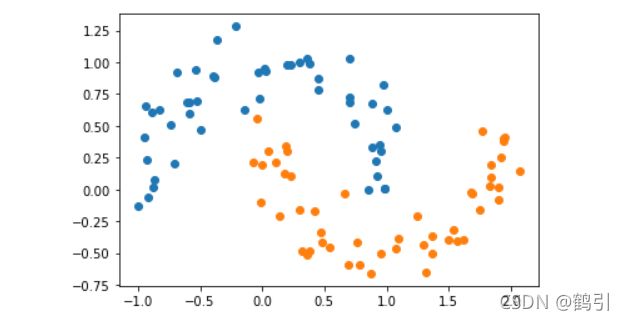
2. 构建月亮数据集并可视化

X, y = datasets.make_moons() #使用生成的数据
#print(X.shape) # (100,2)
#print(y.shape) # (100,)
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

3. 生成噪声点并可视化

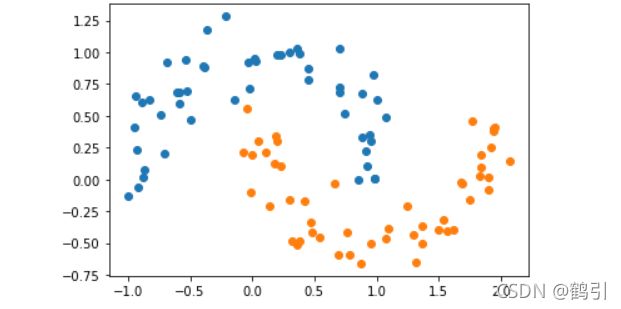
X, y = datasets.make_moons(noise=0.15,random_state=777) #随机生成噪声点，random_state是随机种子，noise是方差
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

4. 定义非线性SVM函数

def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])

5. 调用PolynomialSVC函数进行分类可视化
   • 调用非线性SVM分类，实例化SVC

poly_svc = PolynomialSVC(degree=5)
poly_svc.fit(X,y)
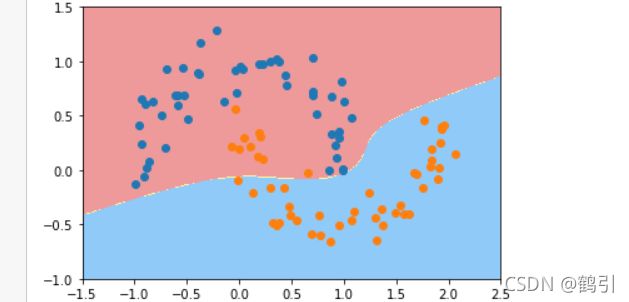
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

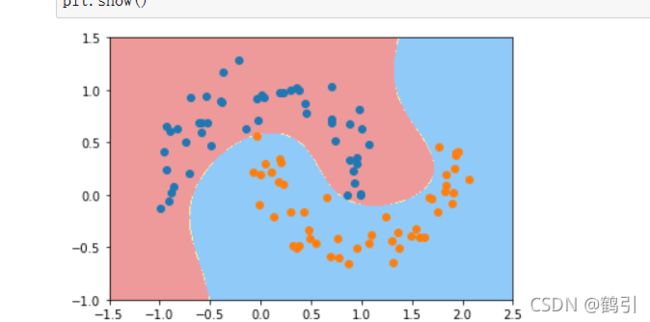
生成的边界不再是线性的直线了，因为月亮数据集提取的两个特征并不是线性的，所以决策边界自然不会是线性
6. 核处理

def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
    ])
poly_kernel_svc = PolynomialKernelSVC(degree=5)
poly_kernel_svc.fit(X,y)
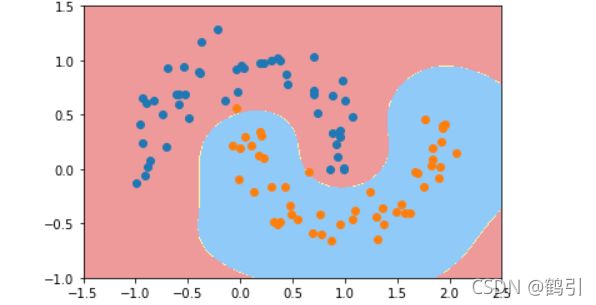
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

此时仍为非线性，但是慢慢趋近于线性

3. 高斯核

1. 导入相应的包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline

2. 导入相应的月亮数据集

X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

3. 定义RBF核的SVM函数

def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

4. 实例化并向γ传递参数
   • γ=200
     
     γ 取值越大，就是高斯分布的钟形图越窄，这里相当于每个样本点都形成了钟形图。很明显这样是过拟合的
   • γ=2
   • γ=0.1
     欠拟合的。我们可以看出γ 值相当于在调整模型的复杂度

svc = RBFKernelSVC(gamma=200)
svc.fit(X,y)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

六、总计

• LDA算法可以用来降维,LDA降维基本也不用调参，只需要指定降维到的维数即可。
• 线性判别的思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异样样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别。

七、参考

线性判别分析（LDA）
【机器学习】机器学习之线性判别分析(LDA)
线性判别分析LDA原理总结
SVM简介
基于jupyter notebook的python编程-----支持向量机学习二（SVM处理线性[鸢尾花数据集]和非线性数据集[月亮数据集]）