基于MAML的改进方法总结

元学习是解决小样本学习问题的重要方法之一，现已取得较为优异的成绩。元学习方法大体上可以分为基于优化的和基于度量两种。基于度量的方法是非参数方法，包括孪生网络、关系网络、匹配网络等。基于优化的方法是参数化方法，典型代表之一是MAML（Model-Agnostic Meta-Learning）。MAML在训练任务上学习一个易于调节的初始化参数，面对新的测试任务时迁移该初始化参数，并利用梯度下降法微调该参数，以达到较好的效果。MAML算法思路简捷、效果优异，近年来产生了诸多变体。下面将带大家梳理其中较为典型的改进方法。

---

MAML算法回顾

MAML

论文地址：https://arxiv.org/pdf/1703.03400.pdf

MAML内层循环（算法流程图中step4-step6）将$\theta$向着最适合每个任务的方向更新为${\theta }_{\mathrm{i}}$（support集上），并在query集上计算损失和。在外层循环（step8）中，利用一批任务的损失共同更新$\theta$。如下所示，(1)是内层更新，(2)是外层更新。值得注意的是，与预训练不同，MAML的初始化参数不是针对当前任务的最优参数，而是最易于调节的参数，该参数只需几步就能在新任务上达到最优，易于调节的性能依赖于在support上训练，在query上更新这一思路。
$${{\theta }_{\mathrm{i}}}^{\prime }=\theta -\alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}(f_{\theta })\text{\hspace{1em}(1)}$$
$$\theta \leftarrow \theta -\beta {\nabla }_{{{\theta }_i}^{\prime }}\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{{\theta }_i}^{\prime }})\text{\hspace{1em}(2)}$$
具体流程如下所示：

FOMAML

原作者在MAML的基础上提出FOMAML，区别在(2)中求导对象不同，FOMAML无需计算二阶导，推导过程利用了多元函数的链式求导法则。
$${{\theta }_{\mathrm{i}}}^{\prime }=\theta -\alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}(f_{\theta })\text{\hspace{1em}(1)}$$
$$\theta \leftarrow \theta -\beta {\nabla }_{{{\theta }_i}^{\prime }}\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{{\theta }_i}^{\prime }})\text{\hspace{1em}(2)}$$

---

从做法来看，MAML的改进策略有传统数理方法（简化二阶导,FOMAML；隐函数积分，iMAML等）、计算机方法（MAML++等）、贝叶斯方法（BMAML等）以及强化学习（ESMAML）、在线学习和其他方法。
然而，这样的分类方法太过冗杂。从解决问题的角度，我将MAML的改进思路分为两种：提高运行速率和提高预测精度。下面依次介绍最经典的几个代表：

提高运行速率

Reptile

论文地址：https://arxiv.org/pdf/1803.02999.pdf

Reptile是最早的改进方法之一。它省略了外层循环，在support∪query集上多次求导,每次求导的方向是Fast weight的方向，其最终的更新方向是多次求导的矢量和与原参数的线性组合，也就是Slow weight的方向。内层循环如下所示：
$$\varphi \leftarrow \varphi +\epsilon \frac{1}{n}\sum _{i=1}^n({\tilde{\varphi }}_i-\varphi )$$

DKT

论文地址：https://arxiv.org/pdf/1910.05199.pdf

算法流程图：
DKT（深度核迁移）方法把模型初始化参数认为是点估计的先验信息，通过先验和似然来估计后验分布。之前的最小化损失函数等价于这里的最大化似然函数。

该方法从贝叶斯定理角度出发，为MAML提供概率解释和不确定性度量。面对新任务时，不光迁移模型初始化参数$\varphi$，同时迁移高斯核参数$\theta$。与Reptile类似，该方法只需一层循环。具体推导采用第二类最大似然法（ML-Ⅱ），把$P({\mathcal{T}}_t^y|{\mathcal{T}}_t^x,\hat{\mathbf{\theta }},\hat{\varphi })$写成积分形式并用条件概率公式展开即可。

本文的另一个创新点在于考虑了跨域问题，即训练任务和测试任务分别取自不同的数据集。

---

提高预测精度

MTNET

论文地址：https://arxiv.org/pdf/1801.05558.pdf

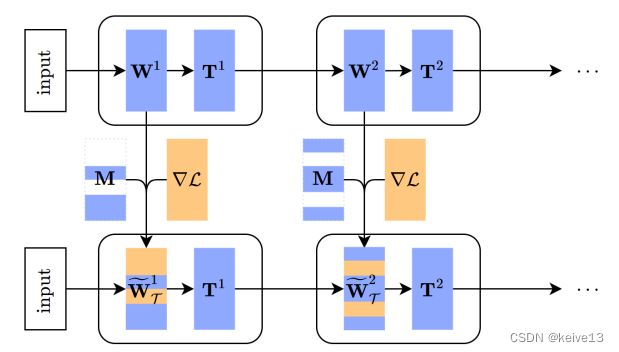
该方法认为外层循环要保证所有任务总损失最小，这样损失了一个自由度，会导致每个任务梯度更新不够灵活。因而在外层循环中再学习一个矩阵(T-net)，相当于对原始参数的线性变换，投影到子空间上。另外，该方法还学习了一类随机变量，该随机变量生成MASK矩阵，决定每个训练任务上更新哪些层，这样减少了过拟合的风险（MT-net）。MT-net如下所示：

CAVIA

论文地址：https://arxiv.org/pdf/1810.03642.pdf

从MAML内外层更新的思路来看，MAML和DKT都假定每个任务的所有参数都是任务特定的，需要在内层循环中更新，而CAVIA则假定每个任务的参数分为任务共享的部分和任务特定的部分。

该方法将需要更新的参数分为任务相关的部分（$\varphi$）和任务共享的部分($\theta$)两种。任务相关的参数又叫上下文参数，只在内层循环中更新，任务共享的参数则在外层循环中更新。对于测试任务，只做内层循环，更新任务特定的部分。这样就避免了过拟合问题。

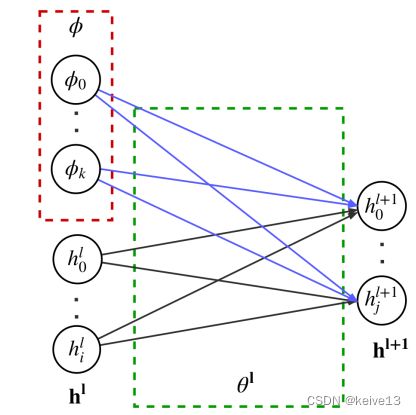
如上图所示，神经元的输入取决于上一层的神经元和上下文参数。
${h_i}^{(l)}=g(\sum _{j=1}^J{{\theta }_{j,i}}^{(l,h)}{h_j}^{\left(l-1\right)}+\sum _{k=1}^K{{\theta }_{k,i}}^{(l,\Phi )}{\Phi }_{0,k}+b)$
作者阐述了该方法在FNN、CNN和RL的应用，在CNN中，作者利用FilM仿射变换（论文地址：https://arxiv.org/pdf/1709.07871.pdf）学习上下文参数。

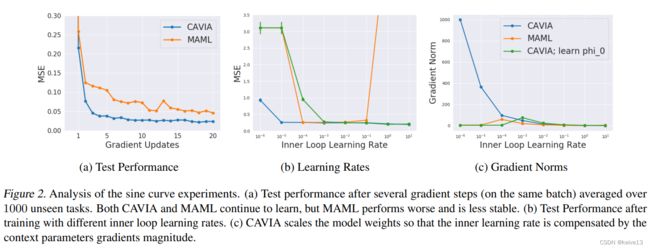
作者在实验中还阐述了CAVIA对内层循环的学习率$\alpha$具有很好的鲁棒性，在sine实验的结果如下图所示：

Pruning

论文地址：https://arxiv.org/pdf/2007.03219.pdf

该方法利用了元学习剪枝的思想，又称为dense-sparse-dense (DSD)。基于Reptile，预训练一个初始化权重，在每个任务上训练时利用MASK选择一部分参数更新，然后再整体训练几轮，这样就减少了任务的过拟合问题。

TAML

论文地址：https://arxiv.org/pdf/1805.07722.pdf

TAML认为不同的任务对优化起的作用是不同的，这种重要性的度量可以用熵变或者经济学中的一些指标度量。算法图如下：


该方法对损失函数稍加改进，有效地平衡了不同任务的贡献度，在分类问题上取得了较为良好的效果。