非极大值抑制(NMS)和soft-nms，及其代码实现

非极大值抑制(NMS)和soft-nms，及其代码实现

NMS算法的大致思想：对于有重叠的候选框：若大于规定阈值（某一提前设定的置信度）则删除，低于阈值的保留。对于无重叠的候选框：都保留。
注释很详细了，应该能看得懂。

# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def NMS(arr, thresh):
    # 首先数据赋值和计算对应矩形框的面积
    # arr的数据格式是arr = [[ xmin, ymin, xmax, ymax,scores]....]

    x1 = arr[:, 0]
    y1 = arr[:, 1]
    x2 = arr[:, 2]
    y2 = arr[:, 3]
    score = arr[:, 4]

    # 所有矩形框的面积
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    # 取出分数从大到小排列的索引。.argsort()是从小到大排列，[::-1]是列表头和尾颠倒一下。
    order = score.argsort()[::-1]
    # 上面这两句比如分数score = [0.72 0.8  0.92 0.72 0.81 0.9 ]
    # 对应的索引order = [2, 5, 4, 1, 3, 0]记住是取出索引，scores列表没变。

    # 这边的keep用于存放，NMS后剩余的方框
    keep = []

    # order会剔除遍历过的方框，和合并过的方框
    while order.size > 0:
        # 取出第一个方框进行和其他方框比对，看有没有可以合并的，就是取最大score的索引
        i = order[0]

        # 因为我们这边分数已经按从大到小排列了。
        # 所以如果有合并存在，也是保留分数最高的这个，也就是我们现在那个这个
        # keep保留的是索引值，不是具体的分数。
        keep.append(i)

        # 计算交集的左上角和右下角
        # 这里要注意，比如x1[i]这个方框的左上角x和所有其他的方框的左上角x的
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        # 这边要注意，如果两个方框相交，xx2-xx1和yy2-yy1是正的。
        # 如果两个方框不相交，xx2-xx1和yy2-yy1是负的，我们把不相交的w和h设为0.
        w = np.maximum(0, xx2-xx1+1)
        h = np.maximum(0, yy2-yy1+1)
        # 计算重叠面积就是上面说的交集面积。不相交因为W和H都是0，所以不相交面积为0
        inter = w * h

        # 这个就是IOU公式（交并比）。
        # 得出来的ious是一个列表，里面拥有当前方框和其他所有方框的IOU结果。
        ious = inter / (areas[i] + areas[order[1:]] - inter)

        # 接下来是合并重叠度最大的方框，也就是合并ious中值大于thresh的方框
        # 我们合并的操作就是把他们剔除，因为我们合并这些方框只保留下分数最高的。
        # 我们经过排序当前我们操作的方框就是分数最高的，所以我们剔除其他和当前重叠度最高的方框
        # 这里np.where(ious<=thresh)[0]是一个固定写法。
        index = np.where(ious <= thresh)[0]

        # 把留下来框在进行NMS操作
        # 这边留下的框是去除当前操作的框，和当前操作的框重叠度大于thresh的框
        # 每一次都会先去除当前操作框（n个框计算n-1个IOU值），所以索引的列表就会向前移动移位，要还原就+1，向后移动一位
        order = order[index+1]

    return keep

def plot_bbox(dets, c='k'):
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]

    plt.plot([x1, x2], [y1, y1], c)
    plt.plot([x1, x1], [y1, y2], c)
    plt.plot([x1, x2], [y2, y2], c)
    plt.plot([x2, x2], [y1, y2], c)
    plt.title(" nms")

if __name__ == '__main__':

    boxes = np.array([[100, 100, 210, 210, 0.72],
                      [250, 250, 420, 420, 0.8],
                      [220, 220, 320, 330, 0.92],
                      [100, 100, 210, 210, 0.72],
                      [230, 240, 325, 330, 0.81],
                      [220, 230, 315, 340, 0.9]])


    plt.figure(1)
    ax1 = plt.subplot(1, 2, 1)
    ax2 = plt.subplot(1, 2, 2)

    plt.sca(ax1)
    plot_bbox(boxes, 'k')  # before nms

    keep = NMS(boxes, thresh=0.7)
    plt.sca(ax2)
    plot_bbox(boxes[keep], 'r')  # after nms
    plt.show()

soft-nms就是在nms的基础上进行了一定程度的改进。

nms有什么问题呢？看一下下面这张图片：

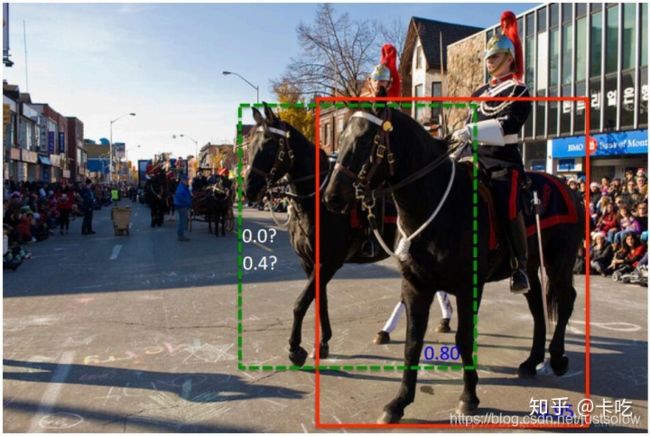
红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。另一方面，NMS的阈值也不太容易确定，设小了会出现下图的情况（绿色框因为和红色框重叠面积较大而被删掉），设置过高又容易增大误检。

解决思路：不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。

soft NMS算法的大致思路为：M为当前得分最高框，bi 为待处理框，bi 和M的IOU越大，bi 的得分si 就下降的越厉害。

下面看一下具体的公式：

NMS中置信度的公式为：

soft-nms中：
（１）线性加权：

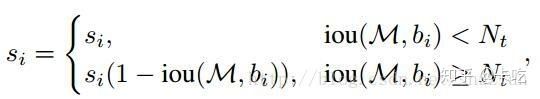
（２）高斯加权：

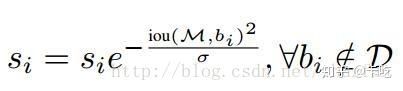
soft NMS仍然有问题：其阈值仍然需要手工设定

soft NMS的相关代码如下：

作者：IronMan
链接：https://zhuanlan.zhihu.com/p/42018282
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

# coding:utf-8
import numpy as np
def soft_nms(boxes, sigma=0.5, Nt=0.1, threshold=0.001, method=1):
    N = boxes.shape[0]
    pos = 0
    maxscore = 0
    maxpos = 0

    for i in range(N):
        maxscore = boxes[i, 4]
        maxpos = i

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # get max box
        while pos < N:
            if maxscore < boxes[pos, 4]:
                maxscore = boxes[pos, 4]
                maxpos = pos
            pos = pos + 1

    # add max box as a detection
        boxes[i,0] = boxes[maxpos,0]
        boxes[i,1] = boxes[maxpos,1]
        boxes[i,2] = boxes[maxpos,2]
        boxes[i,3] = boxes[maxpos,3]
        boxes[i,4] = boxes[maxpos,4]

    # swap ith box with position of max box
        boxes[maxpos,0] = tx1
        boxes[maxpos,1] = ty1
        boxes[maxpos,2] = tx2
        boxes[maxpos,3] = ty2
        boxes[maxpos,4] = ts

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # NMS iterations, note that N changes if detection boxes fall below threshold
        while pos < N:
            x1 = boxes[pos, 0]
            y1 = boxes[pos, 1]
            x2 = boxes[pos, 2]
            y2 = boxes[pos, 3]
            s = boxes[pos, 4]

            area = (x2 - x1 + 1) * (y2 - y1 + 1)
            iw = (min(tx2, x2) - max(tx1, x1) + 1)
            if iw > 0:
                ih = (min(ty2, y2) - max(ty1, y1) + 1)
                if ih > 0:
                    ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
                    ov = iw * ih / ua #iou between max box and detection box

                    if method == 1: # linear
                        if ov > Nt:
                            weight = 1 - ov
                        else:
                            weight = 1
                    elif method == 2: # gaussian
                        weight = np.exp(-(ov * ov)/sigma)
                    else: # original NMS
                        if ov > Nt:
                            weight = 0
                        else:
                            weight = 1

                    boxes[pos, 4] = weight*boxes[pos, 4]
                    print(boxes[:, 4])

            # if box score falls below threshold, discard the box by swapping with last box
            # update N
                    if boxes[pos, 4] < threshold:
                        boxes[pos,0] = boxes[N-1, 0]
                        boxes[pos,1] = boxes[N-1, 1]
                        boxes[pos,2] = boxes[N-1, 2]
                        boxes[pos,3] = boxes[N-1, 3]
                        boxes[pos,4] = boxes[N-1, 4]
                        N = N - 1
                        pos = pos - 1

            pos = pos + 1
    keep = [i for i in range(N)]
    return keep
boxes = np.array([[100, 100, 150, 168, 0.63],[166, 70, 312, 190, 0.55],[221, 250, 389, 500, 0.79],[12, 190, 300, 399, 0.9],[28, 130, 134, 302, 0.3]])
keep = soft_nms(boxes)
print(keep)

参考自：
https://www.zhihu.com/search?type=content&q=soft-nms
https://zhuanlan.zhihu.com/p/128125301