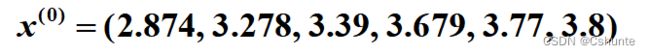Matlab灰色预测GM(1,1)和GM(2,1)对比

  灰色预测的主要特点是模型使用的不是原始数据序列，而是生成的数据序列。其核心体系是灰色模型（Grey Model，简称GM），即对原始数据作累加生成（或其它方法生成）得到近似的指数规律再进行建模的方法。

灰色系统的特点：

     1.数据量太少，不足以用神经网络或者回归等模型

     2.数据及其时间是已知的

     3.数据和时间之间存在内在联系

     4.具体函数关系未知

     5.短期预测（用于预测接下来的几个时间段的数据）

GM(1,1)表示模型是1阶微分方程，且只含1个变量的灰色模型。

GM(2,1)表示模型是2阶微分方程，且只含1个变量的灰色模型。

GM(1,1)适合于指数规律较强的序列，只能描述单调变化过程。对于具有一定随机波动性的序列，我们考虑使用Verhulst预测模型，或者GM(2,1)模型。

Verhulst和GM(2,1)适合于非单调的摆动发展序列或者具有饱和状态的 S 形序列。

下面做二者的对比：

已知序列：

分别建立GM(1,1)、GM(2,1)模型进行预测

①GM(1，1)模型

clc,clear
x0=[2.874 3.278 3.39 3.679 3.77 3.8]';
n=length(x0);
lamda=x0(1:n-1)./x0(2:n)                 %计算级比
range=minmax(lamda')                     %计算级比的范围
x1=cumsum(x0);                           %累加运算
B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];
Y=x0(2:n);
u=B\Y                                    %拟合参数u(1)=a,u(2)=b
x=dsolve('Dx+a*x=b','x(0)=x0');          %求微分方程的符号解
x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)}); %代入估计参数值和初始值
yuce1=subs(x,'t',[0:n-1]);               %求已知数据的预测值
y=vpa(x,6)                                %其中的6表示显示6位数字                
yuce=[x0(1),diff(yuce1)]                  %差分运算，还原数据
epsilon=x0-yuce                           %计算残差
delta=abs(epsilon./x0);                    %计算相对误差
rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda'    %计算级比偏差值，u(1)=a

输出为：

可见该模型达到较高的要求

预测第7个数据：

82.4747*exp(0.0393139*6) - 79.6007-(82.4747*exp(0.0393139*5) - 79.6007)

输出结果：

 ②GM(2,1)模型

clc,clear;
x0=[2.874 3.278 3.39 3.679 3.77 3.8];
n=length(x0);
x1=cumsum(x0)   %计算1次累加序列
a_x0=diff(x0)' %计算1次累减序列
z=0.5*(x1(2:end)+x1(1:end-1))';%计算矩阵序列
B=[-x0(2:end)',-z,ones(n-1,1)];
u=B\a_x0   %最小二乘法拟合参数
syms x(t)
x=dsolve(diff(x,2)+u(1)*diff(x)+u(2)*x==u(3),x(0)==x1(1),x(5)==x1(6));%求符号解
xt=vpa(x,6)
yuce=subs(x,t,0:n-1);     %求已知数据点1次累加序列的预测值
yuce=double(yuce)      %显示6位数字的符号解       得到的y可以用来预测
x0_hat=[yuce(1),diff(yuce)];    %求已知数据点的预测值
x0_hat=round(x0_hat)      %四舍五入取整数
epsilon=x0-x0_hat   %求残差
delta=abs(epsilon./x0)  %求相对误差

输出为：

 可见该模型达到较高的要求

预测第7个数据

38.8692*exp(0.0787376*6) - 0.0398091*exp(0.617978*6) - 35.9554-(38.8692*exp(0.0787376*5) - 0.0398091*exp(0.617978*5) - 35.9554)

输出结果：