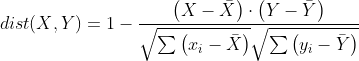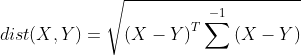机器学习（6）——数据探索与可视化（2）

目录

1 可视化分析数据关系

1.1 连续变量间关系可视化分析

1.1.1 两个连续变量之间的可视化

1.1.2 多个连续变量之间的可视化

1.2 分类变量间关系可视化分析

1.2.1 两个分类变量

1.2.2 多个分类变量

1.3 连续变量和分类变量间关系可视化分析

1.3.1 一个分类变量和一个连续变量

1.3.2 两个分类变量和一个连续变量

1.3.3 两个分类变量和两个连续变量

1.3.4 一个分类变量和多个连续变量

1.4 其他类型数据可视化分析

1.4.1 时间序列数据

1.4.2 文本数据

 1.4.3 社交网络数据

2 数据样本间的距离

2.1 欧氏距离和曼哈顿距离

2.2 切比雪夫距离和余弦距离

2.3 相关系数距离和马氏距离

---

注意：本篇博文中所记录的笔记中尚存一些问题，已用红色字体标示出。

1 可视化分析数据关系

本节将会根据不同的数据类型，使用合适的数据可视化方法，对数据进行分析。针对不同的可视化图像，会尽可能地使用相对简单的可视化方式进行数据可视化。在进行数据可视化时，分为连续变量间关系可视化分析、分类变量间关系可视化、连续变量和分类变量间关系可视化分析，以及其他类型数据可视化分析。

1.1 连续变量间关系可视化分析

当待分析的数据均为连续变量时，由于数据变量的数目不同和想要从数据中获取信息的目的不同，可以使用不同的可视化方法。下面以鸢尾花数据集为例：

Iris.csv文件链接：

链接：https://pan.baidu.com/s/1TEq5SxWyi-6deYixjP_s8Q 
提取码：whj6

import pandas as pd
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
print(Iris2.head(3))

运行结果如下：

SepalLengthCm  SepalWidthCm  PetalLengthCm  PetalWidthCm
0            5.1           3.5            1.4           0.2
1            4.9           3.0            1.4           0.2
2            4.7           3.2            1.3           0.2

1.1.1 两个连续变量之间的可视化

对于两个连续数值变量之间的可视化方式，最直观的就是使用散点图进行可视化分析。下面对于鸢尾花数据集中的SepalLengthCm和SepalWidthCm变量，使用以下程序得到散点图：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
plt.figure(figsize=(10,6))
sns.scatterplot(x="SepalLengthCm",y="SepalWidthCm",data=Iris2,s=50)
plt.grid()
plt.title('散点图')
plt.show()

运行结果如下：

 两个连续变量之间的可视化

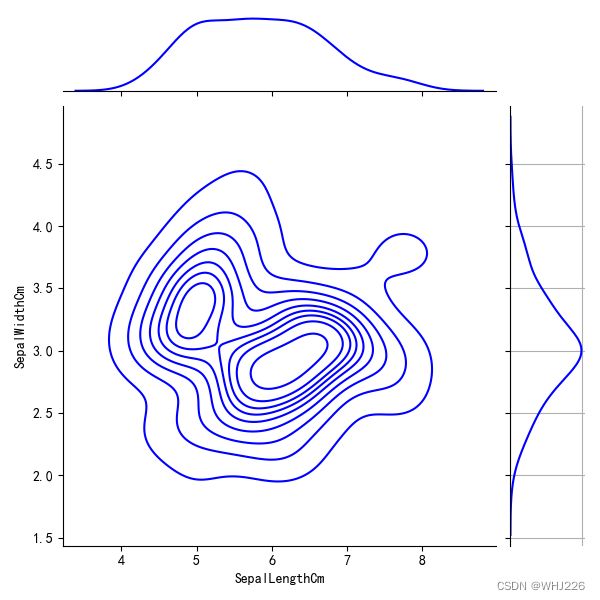
从散点图中很容易分析两个变量之间的变化趋势，如果想要分析两个变量在空间中的分布情况，可以使用2D密度曲线图进行可视化分析。

#2D密度曲线
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
sns.jointplot(x="SepalLengthCm",y="SepalWidthCm",data=Iris2,kind='kde',color='blue')
plt.grid()
plt.show()

运行结果如下：

 2D密度曲线图

2D密度曲线图中不同位置，数据分布的密度是不一样的，同时在图的右侧和上方，分别可视化出了两个变量的一维密度曲线，用于帮助分析数据的分布情况。

针对两个数值变量，如果想要分析两者在各自的一维空间上分布情况差异，可以使用分组直方图可视化出两组数据在同一坐标系下的分布情况。

#直方图
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
Iris2.iloc[:,0:2].plot(kind='hist',bins=30,figsize=(10,6))
plt.grid()
plt.title('分组直方图')
plt.show()

运行结果如下：

从运行结果来看，两个变量的数据分布位置和范围都很容易比较，而且还可以发现两者数据聚集情况的差异，其中变量SepalLengthCm的取值范围比变量SepalWidthCm大，位置也更集中，但是SepalWidthCm的分布更加聚集。

1.1.2 多个连续变量之间的可视化

针对多个连续变量之间的数据可视化，通常会使用气泡图、小提琴图、蒸汽图等对数据进行可视化分析。

气泡图通常用于3个变量的可视化，其中两个变量表示点所在的位置，另一个变量使用点的大小反映数据取值大小，从而可以在二维空间中分析3个变量之间的关系。

#气泡图
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
plt.figure(figsize=(10,6))
sns.scatterplot(x="PetalWidthCm",y="SepalWidthCm",data=Iris2,
                size="SepalLengthCm",sizes=(20,200),palette="muted")
plt.title('气泡图')
plt.legend(loc="best")
plt.grid()
plt.show()

运行结果如下：

变量PetalWidthCm和变量SepalWidthCm用于指定点在空间中的位置，而气泡的大小使用变量SepalLengthCm表示。从图中可以发现，变量PetalWidthCm和变量SepalWidthCm的取值越大，所对应的气泡也越大。

如果想要分析多个变量之间数据分布趋势的差异，则可以使用小提琴图进行分析，在小提琴图中可以获取数据的取值范围、集中位置、离散情况等，并且还可以同时将多个变量的小提琴图可视化在一幅图中，用于分析多个变量的分布差异等内容。

#使用小提琴图分析数据取值上的差异
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Iris2 = Iris.drop(["Id","Species"],axis=1)
plt.figure(figsize=(10,6))
sns.violinplot(data=Iris2.iloc[:,0:4],palette="Set3",bw=0.5)
plt.title('小提琴图')
plt.grid()
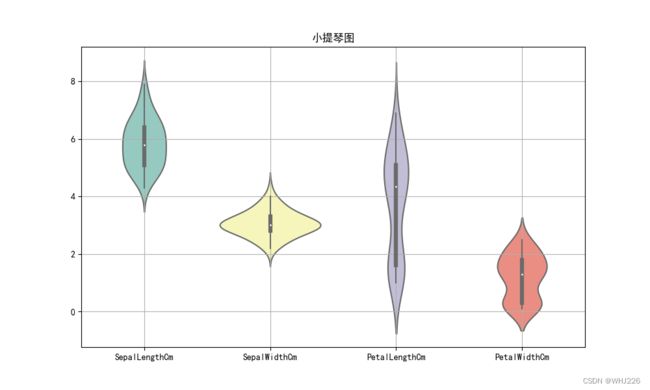
plt.show()

 运行结果如下：

从图中可以发现，数据的离散程度从小到大以此是：SepalWidthCm、PetalLengthCm、SepalLengthCm、PetalWidthCm，而且数据中PetalLengthCm变量和PetalWidthCm变量的分布为双峰图。

对于多个连续变量，也可以使用蒸汽图分析随着样本量的增加（或者时间的增长），数据取值的变化情况。（此处翻车了，在查找错误处，错误现象是无法显示蒸汽图）

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import altair as alt
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Irislong = Iris.melt(["Id","Species"],var_name="Measurement_type",value_name="value")
print(Irislong.head())
#蒸汽图可视化
alt.Chart(Irislong).mark_area().encode(
    alt.X("Id:Q"), #X轴
    alt.Y("value:Q",stack="center",axis=None), #Y轴
    alt.Color('Measurement_type:N') #设置颜色
).properties(width=500,height=300) #设置图形大小

运行结果如下：

Id Species Measurement_type  value
0   1  setosa    SepalLengthCm    5.1
1   2  setosa    SepalLengthCm    4.9
2   3  setosa    SepalLengthCm    4.7
3   4  setosa    SepalLengthCm    4.6
4   5  setosa    SepalLengthCm    5.0

在上面的程序中，在使用鸢尾花数据之前，先对其使用melt()方法，将宽数据转化为长数据，因此在获得长数据Irislong中，变量Measurement_type表明了使用的特征名，value对应着原始特征的相应取值。

1.2 分类变量间关系可视化分析

首先导入待分析的泰坦尼克号数据：

链接：https://pan.baidu.com/s/1RSD9gfUNRqsdSimkY1wQlA 
提取码：whj6

import pandas as pd
#读取演示数据
Titanic = pd.read_csv("E:/PYTHON/Titanic数据.csv")
print(Titanic.head())

运行结果如下：

   Pclass   Name     Sex   Age  SibSp  Parch     Fare Embarked  Survived
0       3    Mr.    male  22.0      1      0   7.2500        S         0
1       1   Mrs.  female  38.0      1      0  71.2833        C         1
2       3  Miss.  female  26.0      0      0   7.9250        S         1
3       1   Mrs.  female  35.0      1      0  53.1000        S         1
4       3    Mr.    male  35.0      0      0   8.0500        S         0

由运行结果来看，导入的数据包含多个分类变量，针对分类变量数量的不同，可以使用不同的可视化方法进行数据分析。

1.2.1 两个分类变量

以Titanic数据中的变量Embarked和Survived为例，可以使用数据列联表查看每种组合下的样本数量，也可以使用卡方检验分析两个变量是否独立。

import pandas as pd
from scipy.stats import chi2_contingency
#读取演示数据
Titanic = pd.read_csv("E:/PYTHON/Titanic数据.csv")
#print(Titanic.head())
#卡方检验
tab = pd.crosstab(Titanic["Embarked"],Titanic["Survived"])
print(tab)
c,p,_,_= chi2_contingency(tab.values)
print("卡方值:", c, ";P value:", p)

运行结果如下：

Survived    0    1
Embarked          
C          75   93
Q          47   30
S         427  219
卡方值: 25.964452881874784 ;P value: 2.3008626481449577e-06

从上面的输出结果可以发现，卡方检验的P值远小于0.05，说明两个变量不是独立的，即有些相关性。针对两个变量之间的相关性情况，可以使用马赛克图进行可视化分析，如下：

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.mosaicplot import mosaic
#图像显示中文设置
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#读取演示数据
Titanic = pd.read_csv("E:/PYTHON/Titanic数据.csv")
#马赛克图
mosaic(Titanic,["Embarked","Survived"],gap=0.01,title="马赛克图")
plt.show()

运行结果如下：

从图中可以发现，当变量Embarked的取值为S或者Q时，Survived取值为1所占的比例就更低。

1.2.2 多个分类变量

针对多个分类变量的关系，可以使用树图进行可视化分析，树图使用矩形来表示数量的多少，可对数据进行逐层分组可视化，如下:

#图像显示中文设置
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
#导入要使用的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
import altair as alt
from statsmodels.graphics.mosaicplot import mosaic
from scipy.stats import chi2_contingency
import plotly.express as px
from pandas.plotting import parallel_coordinates
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
from scipy.spatial import distance

#读取演示数据
Titanic = pd.read_csv("E:/PYTHON/Titanic数据.csv")
#树图
Titanic["Titanic"] = "Titanic"
Titanic["value"] = 1
fig = px.treemap(Titanic,path=["Titanic","Survived","Sex","Embarked"],
                 values="value",color="Fare",color_continuous_scale="RdBu",width=800,height=500)
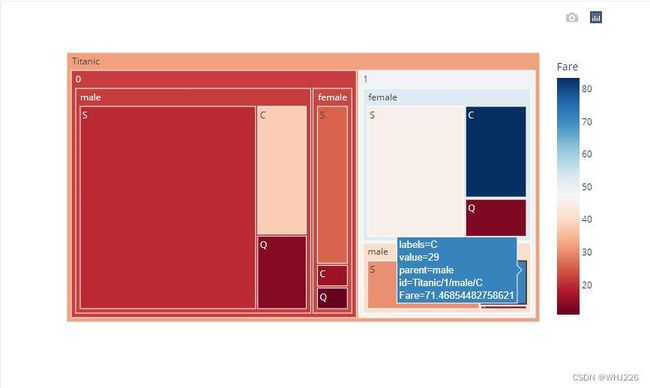
fig.show()

运行结果如下：（下图在浏览器中生成）

从图中运行结果可以发现，遇难者明显多于幸存者；票价（Fare）低的乘客更容易遇难；在遇难的人员中，男性远远多于女性；在幸存的人员中，女性远远多于男性。使用Plotly包获得的图像是可交互的图像，可以通过单击对图像进行更多查看和对比分析。

1.3 连续变量和分类变量间关系可视化分析

在数据分析过程中，很少会有只包含连续变量或者分类变量的情况，通常待分析的数据会同时包含连续变量和分类变量。前面变换得到的鸢尾花长型数据集Irislong，就包含多个分类变量和连续变量。下面使用该数据集展示：

1.3.1 一个分类变量和一个连续变量

如果要分析长型鸢尾花数据中的一个分类变量和一个连续变量之间的关系，可以使用箱线图。它可以分析在不同分类变量下，连续变量的分布情况。

首先，基本设置和所需包的导入如下：（后面出现新模块时再添加，否则以下所有程序默认包含以下程序）：

#图像显示中文设置
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
#导入要使用的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
import altair as alt
from statsmodels.graphics.mosaicplot import mosaic
from scipy.stats import chi2_contingency
import plotly.express as px
from pandas.plotting import parallel_coordinates
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
from scipy.spatial import distance

对于Irislong数据表，使用箱线图可视化变量Species和变量value之间的关系：

#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Irislong = Iris.melt(["Id","Species"],var_name="Measurement_type",value_name="value")
#分组箱线图
plt.figure(figsize=(10,6))
sns.boxplot(data=Irislong,x="Species",y="value")
plt.title('分组箱线图')
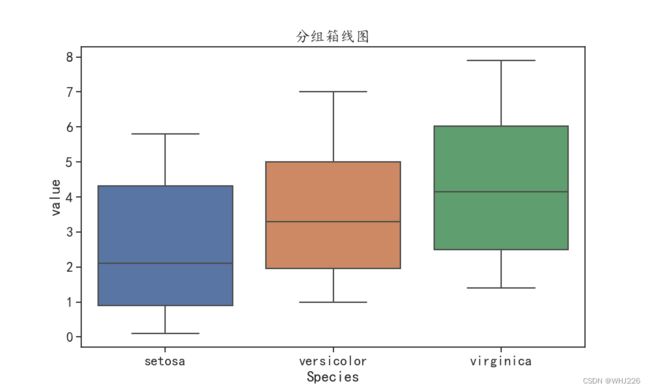
plt.show()

运行结果如下：

从图中可以看出，三者的取值极差相近，但是数据的集中位置逐次升高。

一个分类变量和一个连续变量，还可以使用分面密度曲线图查看数据的分布。以长型鸢尾花数据为例，可以使用Measurement_type变量进行分面，分析value变量的数据分布情况。

#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Irislong = Iris.melt(["Id","Species"],var_name="Measurement_type",value_name="value")
#分面密度曲线查看数据分布
alt.Chart(Irislong).transform_density(
    density="value",bandwidth=0.3,
    groupby=["Measurement_type"],extent=[0,8]
).mark_area().encode(
    alt.X("value:Q"), #X轴
    alt.Y("density:Q"), #Y轴
    alt.Row('Measurement_type:N'),
).properties(width=500,height=80) #设置图形大小

出现了和蒸汽图同样的问题（待解决）

1.3.2 两个分类变量和一个连续变量

对于数据中包含两个分类变量和一个连续变量的情况，可以使用分组箱线图对数据进行可视化，即一个分组变量作为箱线图的横坐标变量，另一个变量作为对应x轴坐标的再次分割变量。

## 分组箱线图
#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
Irislong = Iris.melt(["Id","Species"],var_name="Measurement_type",value_name="value")
plt.figure(figsize=(10,6))
sns.boxplot(data = Irislong,x = "Measurement_type",y = "value",hue = "Species")
plt.legend(loc = 1)
plt.title("分组箱线图")
plt.show()

运行结果如下：

从图中可以发现，value的分布不仅受Measurement_type取值的影响，而且变量Species的取值也对数据value的分布有较大的影响。

1.3.3 两个分类变量和两个连续变量

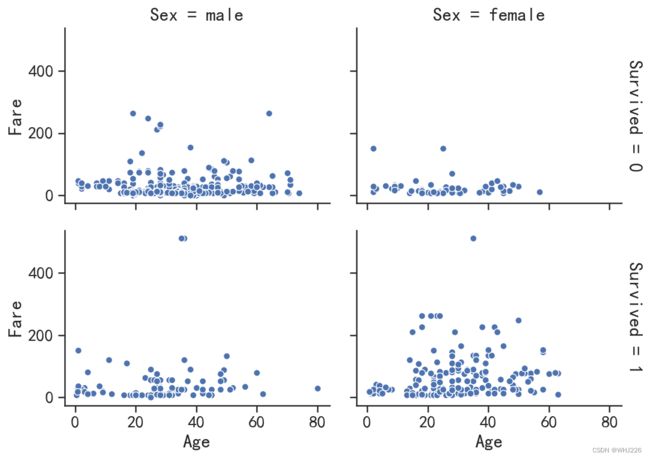
如果想要可视化两个分类变量和两个连续变量之间的关系，可以使用分面散点图，其中两个分类变量将可视化界面切分为网格，然后再对应的网格下面可视化出两个连续变量的散点图，从而对数据进行对比分析。下面将对泰坦尼克号数据中的两个分类变量和两个连续变量进行可视化：

#读取演示数据
Titanic = pd.read_csv("E:/PYTHON/Titanic数据.csv")
## 分面散点图
## 设置网格分面
g = sns.FacetGrid(data = Titanic,row="Survived",col="Sex",
                  margin_titles=True,height=3,aspect=1.4)
## 添加散点图
g.map(sns.scatterplot,"Age" ,"Fare")
plt.show()

运行结果如下：（如出现图像闪退的话只需要在读取数据下面添加一行代码，此处可解决闪退）

plt.figure(figsize=(10,7))

1.3.4 一个分类变量和多个连续变量

对于一个分类变量和多个连续变量的数据可视化方法，最常用的就是使用平行坐标图，其中每个连续变量是横轴中的一个坐标点，其取值大小则标记在对应的竖直线上，可以使用颜色为分组变量中的每条平行线进行分组编码。对于鸢尾花数据集的4个连续变量和1个分类变量，使用下面的程序可以获得平行坐标图：

#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
## 平行坐标图
plt.figure(figsize=(10,6))
parallel_coordinates(Iris.iloc[:,1:6], "Species",alpha = 0.8)
plt.title("平行坐标图")
plt.show()

运行结果如下：

从运行结果来看，3种不同的花在PetalLengthCm变量上的差异最大，而在SepalWidthCm变量上的差异性最小。

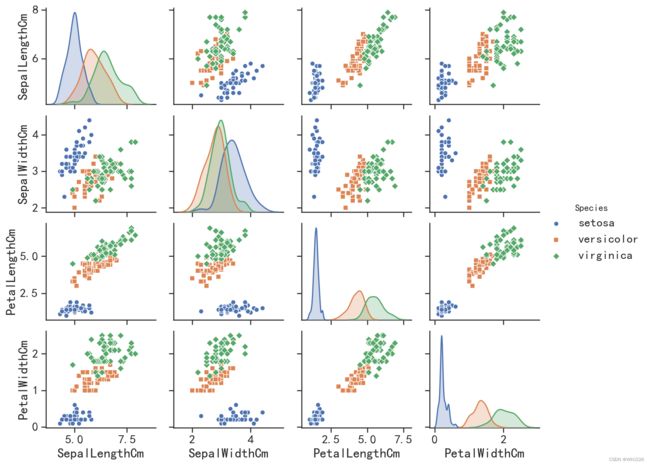
对于一个分类变量和多个连续变量的数据，如果想要分析不同分类变量下，连续变量之间的关系，可以使用矩阵散点图进行数据可视化。针对鸢尾花数据使用矩阵散点图进行数据可视化：

#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
## 矩阵散点图
sns.pairplot(Iris.iloc[:,1:6],hue="Species",height=2,aspect=1.2,
             diag_kind="kde",markers=["o", "s", "D"])
plt.show()

 运行结果如下：

 （如出现图像闪退的话只需要在读取数据下面添加一行代码，此处可解决闪退）

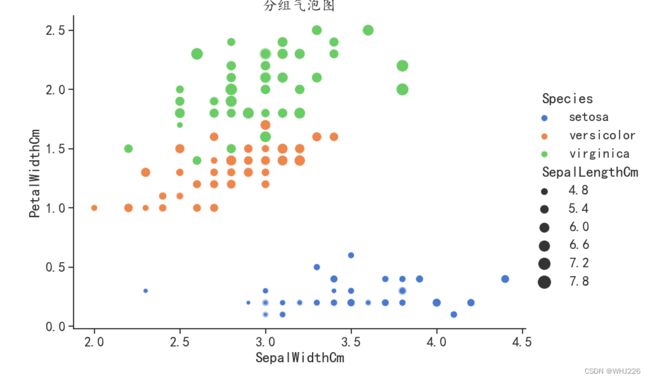
plt.figure(figsize=(10,7))

气泡图可以可视化3个数值变量之间的关系，如果添加一个分类变量，对数据进行可视化，可以获得分组气泡图，也可以用于分析分组数据对其他数值之间关系的影响。

#读取鸢尾花数据集
Iris = pd.read_csv("E:/PYTHON/Iris.csv")
## 分组气泡图
plt.figure(figsize=(10,7))
sns.relplot(data = Iris, x="SepalWidthCm", y="PetalWidthCm",
            hue="Species", size = "SepalLengthCm",sizes = (20,200),
            palette="muted",height=6,aspect = 1.4)
plt.title("分组气泡图")
plt.show()

  运行结果如下：

 在该图中，使用了不同的颜色对气泡进行分组，用于发现不同组内数据关系和组间数据差异。

1.4 其他类型数据可视化分析

1.4.1 时间序列数据

对于时间序列数据，可以使用散点图和折线图等进行可视化，但是需要注意的是，时间序列数据的可视化图像中，x轴通常表示时间的变化，而且有顺序，所以位置不能随意变化，否则将不具有其原有的数据含义。

OpenPowerSystemData.csv提取链接：

链接：https://pan.baidu.com/s/1S0NFkVpuu8LR5YGba5pvpw 
提取码：whj6

## 时间序列数据
opsd = pd.read_csv("E:/PYTHON/OpenPowerSystemData.csv")
opsd.head()
## 折线图
opsd.plot(kind = "line",x = "Date",y = "Solar",figsize = (10,6))
plt.ylabel("Value")
plt.title("时间序列曲线")
plt.show()

运行结果如下：

1.4.2 文本数据

文本数据是常见的非结构化数据，其常用的数据可视化方法是词云，利用词云来描述词语出现的频繁程度。下面以《三国演义》的文本内容为例，统计出每个词语出现的频次，然后使用词云进行可视化：

三国演义分词后.csv提取链接：

链接：https://pan.baidu.com/s/1g8_tiDTnKCCBQ7k_0xkdqA 
提取码：whj6 

from wordcloud import WordCloud #新导入模块
## 文本数据
## 词云可视化

## 准备数据
TKing = pd.read_csv("E:/PYTHON/三国演义分词后.csv")
## 计算每个词语出现的频次
TK_fre = TKing.x.value_counts()
TK_fre = pd.DataFrame({"word":TK_fre.index,
                       "Freq":TK_fre.values})
## 去除出现次数较少的词语
TK_fre = TK_fre[TK_fre.Freq > 100]
TK_fre
## 可视化词云
## 将词和词频组成字典数据准备
worddict = {}
for key,value in zip(TK_fre.word,TK_fre.Freq):
    worddict[key] = value
## 生成词云
redcold = WordCloud(font_path="/Library/Fonts/Microsoft/SimHei.ttf",
                    margin=5,width=1800, height=1000,
                    max_words=400, min_font_size=5,
                    background_color='white',
                    max_font_size=250,)
redcold.generate_from_frequencies(frequencies=worddict)
plt.figure(figsize=(10,7))
plt.imshow(redcold)
plt.axis("off")
plt.show()

font_path参数指定合适的字体，使用generate_from_frequencies方法传入准备好的字典。其他参数width=1800, height=1000用来指定图像的大小，max_words指定最多显示多少个词语，max_font_size指定词语最大的尺寸。

运行结果如下：（因安装wordcloud包失败无法运行，但下图是成功运行后的结果）

1.4.3 社交网络数据

也可以使用图可视化社交网络数据。图由边和节点组成，每条边表示其所连接的两个节点之间的联系，针对数据可以使用networkx库可视化，下面先导入空手道俱乐部的社交网络数据：

karate.csv提取链接：

链接：https://pan.baidu.com/s/1F9EQPYx8psynu_3ygxzoGw 
提取码：whj6

## 读取网络数据
karate = pd.read_csv("E:/PYTHON/karate.csv")
print(karate.head())

运行结果如下：

From       to  weight
0  Mr Hi  Actor 2       4
1  Mr Hi  Actor 3       5
2  Mr Hi  Actor 4       3
3  Mr Hi  Actor 5       3
4  Mr Hi  Actor 6       3

在karate数据中，From和to两个变量表示两个节点的一条边，weight变量表示两个节点之间的权重，可视化程序如下：

## 读取网络数据
karate = pd.read_csv("E:/PYTHON/karate.csv")
#print(karate.head())
## 网络图数据可视化
plt.figure(figsize=(12, 8))
## 生成社交网络图
G = nx.Graph()

## 为图像添加边
for ii in karate.index:
    G.add_edge(karate.From[ii], karate.to[ii], weight=karate.weight[ii])

## 根据权重大小定义2种边
elarge = [(u, v) for (u, v, d) in G.edges(data=True) if d['weight'] > 3.5]
esmall = [(u, v) for (u, v, d) in G.edges(data=True) if d['weight'] < 3.5]

## 图的布局方式
pos = graphviz_layout(G, prog="fdp")
# pos=nx.circular_layout(G)

# 可视化图的节点
nx.draw_networkx_nodes(G, pos, alpha=0.4, node_size=20)

# 可视化图的边
nx.draw_networkx_edges(G, pos, edgelist=elarge,
                       width=2, alpha=0.5, edge_color="red")
nx.draw_networkx_edges(G, pos, edgelist=esmall,
                       width=2, alpha=0.5, edge_color="blue", style='dashed')

# 为节点添加标签
nx.draw_networkx_labels(G, pos, size=16)
plt.axis('off')
plt.title("空手道俱乐部人物关系")
plt.show()

运行结果如下：（再次运行失败，同样的问题，下图为正确运行结果）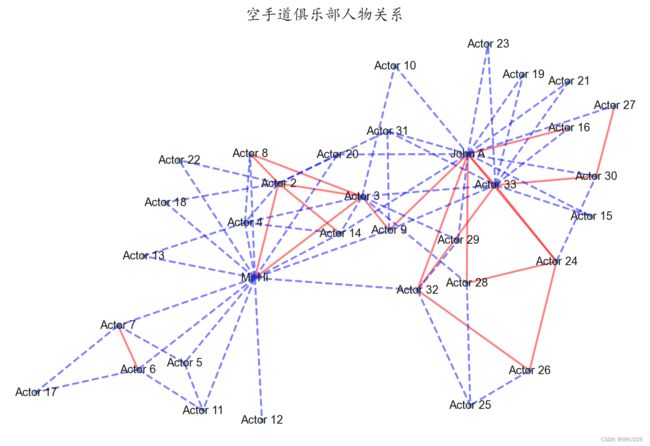

在上面的程序中，先使用G = nx.Graph()定义一个图，并使用G.add_edge()增加有关联的成员之间的边，分别指定边的起点、终点和权重；根据权重将成员之间的边分为两种类型（elarge和esmall）较大的权重（大于3.5）用实线表示，较小的权重（小于3.5）用虚线表示；用nx.draw_networkx_nodes()函数绘制图的节点，并且指定节点图像的大小等性质；用nx.draw_networkx_edges()函数绘制图的边，可以指定边的线宽、颜色、线形等属性；用nx.draw_networkx_labels()函数为节点添加标签。

2 数据样本间的距离

对于给定的数据样本，每个样本都具有多个特征，因此每个样本均是高维空间的一个点，那么在高维空间中如何比较样本之间的距离远近或相似程度呢？

2.1 欧氏距离和曼哈顿距离

下面我们用种子数据集进行试验：

链接：https://pan.baidu.com/s/1W1eXQdfbGao2qmXIfMz28g 
提取码：whj6

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
print(datadf2.head())

运行结果如下：

      x1     x2      x3     x4     x5     x6     x7
0  15.26  14.84  0.8710  5.763  3.312  2.221  5.220
1  14.88  14.57  0.8811  5.554  3.333  1.018  4.956
2  14.29  14.09  0.9050  5.291  3.337  2.699  4.825
3  13.84  13.94  0.8955  5.324  3.379  2.259  4.805
4  16.14  14.99  0.9034  5.658  3.562  1.355  5.175

对于该数据，可以使用多种距离度量方式，比较每个种子样本之间的关系。首先计算的是欧氏距离和曼哈顿距离。

欧氏距离用来度量欧几里得空间中两点间的直线距离，即对于n维空间中的两点，，他们之间的欧氏距离定义为：

曼哈顿距离用以表明两个点在标准坐标系上的绝对轴距的总和，即对于n维空间中的两点，，他们之间的曼哈顿距离定义为：

对于种子数据的这两种距离，可以使用distance.cdist()函数进行计算。下面的程序不仅计算出数据中样本的距离，还是用热力图将距离矩阵进行可视化：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
## 欧式距离
dist = distance.cdist(datadf2,datadf2,"euclidean")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间欧式距离")
plt.show()

运行结果如下：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
# ## 欧式距离
# dist = distance.cdist(datadf2,datadf2,"euclidean")
# ## 使用热力图可视化样本之间的距离
# plt.figure(figsize=(8,6))
# sns.heatmap(dist,cmap="YlGnBu")
# plt.title("样本间欧式距离")
# plt.show()
## 曼哈顿距离
dist = distance.cdist(datadf2,datadf2,"cityblock")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间曼哈顿距离")
plt.show()

 运行结果如下：

这两张图中，这两种距离在整体分布上是一致的，但是距离大小的取值不尽相同。而且在对角线周围形成了3个距离较近的对角块，而每个块和其它块的距离较远，说明针对该数据使用聚类算法，将其分为3类较合适。 

2.2 切比雪夫距离和余弦距离

切比雪夫距离即为两个点之间各个坐标数值差的最大值，即对于n维空间中的两点，，他们之间的切比雪夫距离定义为：

余弦相似性是通过测量两个向量夹角的余弦值来度量他们之间的相似性， 即对于n维空间中的两点，，他们之间的余弦距离定义为：

下面的程序不仅计算出数据中样本的距离，还是用热力图将距离矩阵进行可视化：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
## 切比雪夫距离
dist = distance.cdist(datadf2,datadf2,"chebyshev")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间切比雪夫距离")
plt.show()

运行结果如下：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
# ## 切比雪夫距离
# dist = distance.cdist(datadf2,datadf2,"chebyshev")
# ## 使用热力图可视化样本之间的距离
# plt.figure(figsize=(8,6))
# sns.heatmap(dist,cmap="YlGnBu")
# plt.title("样本间切比雪夫距离")
# plt.show()
## 余弦距离
dist = distance.cdist(datadf2,datadf2,"cosine")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间余弦距离")
plt.show()

 运行结果如下：

数据的切比雪夫距离的分布趋势和前面的两种数据分布较为一致，而样本间的余弦距离则有了较大的差异，形成了一大一小的对角矩阵块。

2.3 相关系数距离和马氏距离

相关系数距离是根据相关性定义的，数值越大距离越远，即对于n维空间中的两点，，他们之间的相关系数距离定义为：

马氏距离表示数据的协方差距离。它是一种有效地计算两个未知样本集相似度的方法。 对于n维空间中的两点，，他们之间的马氏距离定义为：

下面的程序不仅计算出数据中样本的距离，还是用热力图将距离矩阵进行可视化：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
## 相关系数距离
dist = distance.cdist(datadf2,datadf2,"correlation")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间相关系数距离")
plt.show()

 运行结果如下：

## 使用计算距离的数据
datadf = pd.read_csv("E:/PYTHON/种子数据.csv")
datadf2 = datadf.iloc[:,0:7]
# ## 相关系数距离
# dist = distance.cdist(datadf2,datadf2,"correlation")
# ## 使用热力图可视化样本之间的距离
# plt.figure(figsize=(8,6))
# sns.heatmap(dist,cmap="YlGnBu")
# plt.title("样本间相关系数距离")
# plt.show()

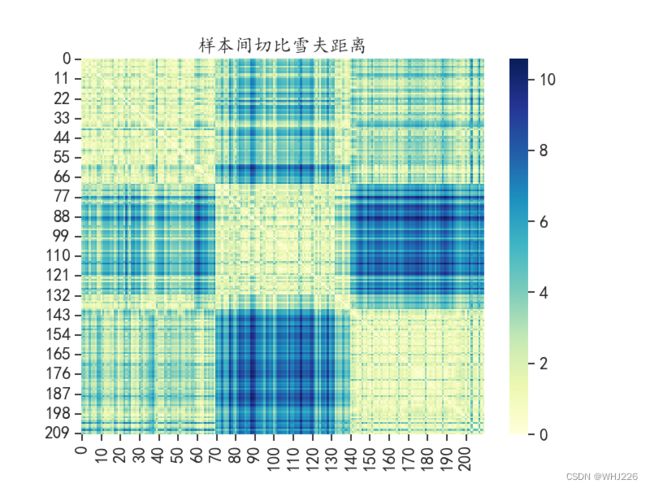
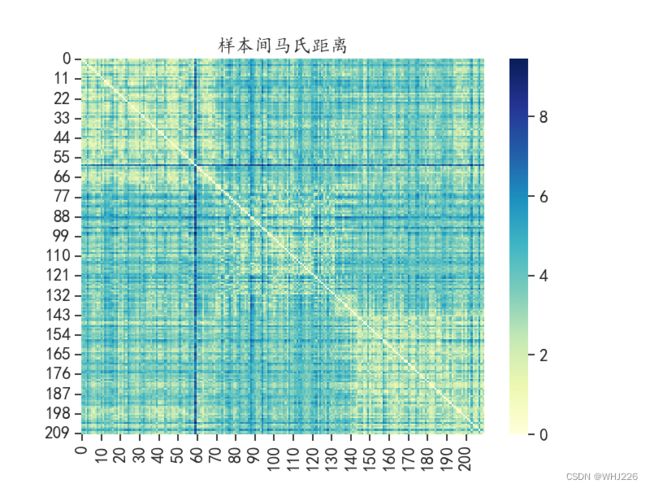
## 马氏距离
dist = distance.cdist(datadf2,datadf2,"mahalanobis")
## 使用热力图可视化样本之间的距离
plt.figure(figsize=(8,6))
sns.heatmap(dist,cmap="YlGnBu")
plt.title("样本间马氏距离")
plt.show()

 运行结果如下：

数据的相关系数距离的分布趋势和前面的余弦距离的分布较一致，样本间的马氏距离则又呈现出一种新的距离大小分布情况。 

笔记摘自——《Python机器学习算法与实战》