B站吴恩达深度学习视频笔记(5)——二分类问题
前言
这几天在努力攻克神经网络,并想办法怎么把那些非常吓人的推到公式变成大家喜欢看的形式,用大家熟知的语言描述出来。很多人都是在神经网络这里看到一大坨公式然后知难而退。神经网络是机器学习的必经之路,是初学者们必须攻克的第一个难题,我会尽量用你们容易接受的语言和知识向你们描述神经网络中的一些最最基础也是最最重要的部分。现在我们来了解一下深度学习中比较简单的一类问题:二分类问题。
二分类(Binary Classification)
吴恩达老师的视频讲二分类问题的角度虽然比较专业,但是还是很容易理解的,这里面会有一些你们可能理解不是很深刻的名词,如果你觉得困难的话,不如先等几天,看完我介绍神经网络再来参考这篇博文学习二分类问题。
本篇博文还是以吴恩达老师的视频为基础
我们将学习神经网络的基础知识,其中需要注意的是,当实现一个神经网络的时候,我们需要知道一些非常重要的技术和技巧。例如有一个包含m个样本的训练集,你很可能习惯于用一个for循环来遍历训练集中的每个样本(适用于有编程思维和经验的人),但是当实现一个神经网络的时候,我们通常不直接使用for循环来遍历整个训练集,所以在这周的课程中你将学会如何处理训练集。
另外在神经网络的计算中,通常先有一个叫做**前向暂停(forward pause)或叫做前向传播(foward propagation)的步骤,接着有一个叫做反向暂停(backward pause) 或叫做反向传播(backward propagation)**的步骤。
所以这周也会向你介绍为什么神经网络的训练过程可以分为前向传播和反向传播两个独立的部分。
在课程中我将使用**逻辑回归(logistic regression)**来传达这些想法,以使大家能够更加容易地理解这些概念。即使你之前了解过逻辑回归,我认为这里还是有些新的、有趣的东西等着你去发现和了解,所以现在开始进入正题。
逻辑回归是一个用于二分类(binary classification)的算法。
二分类问题示例:
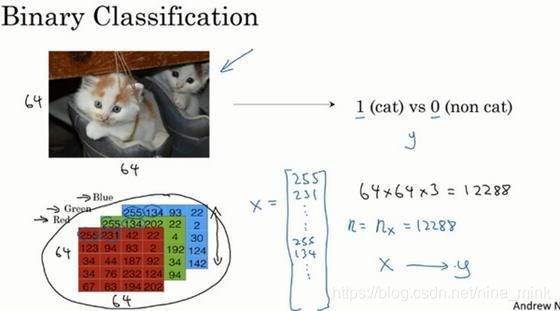
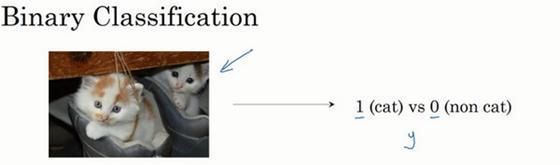
首先我们从一个问题开始说起,这里有一个二分类问题的例子,假如你有一张图片作为输入,比如这只猫,如果识别这张图片为猫,则输出标签1作为结果;如果识别出不是猫,那么输出标签0作为结果(这也就是著名的cat和non cat问题)。现在我们可以用字母y来表示输出的结果标签,如下图所示:
我们来看看一张图片在计算机中是如何表示的,为了保存一张图片,需要保存三个矩阵(矩阵的概念,一定要清楚,不清楚的需要去看看线性代数了,补充下,推荐B站宋浩老师的线性代数,我看了他的视频线代考了96分),它们分别对应图片中的红、绿、蓝三种颜色通道,如果你的图片大小为64x64像素,那么你就有三个规模为64x64的矩阵,分别对应图片中红、绿、蓝三种像素的强度值。为了便于表示,这里我画了三个很小的矩阵,注意它们的规模为5x4 而不是64x64,如下图所示:
 为了把这些像素值放到一个特征向量(这个是重点,特征向量!这个是后面很多神经网络的核心思维!)中,我们需要把这些像素值提取出来,然后放入一个特征向量x。为了把这些像素值转换为特征向量 x,我们需要像下面这样定义一个特征向量 x 来表示这张图片,我们把所有的像素都取出来,例如255、231等等,直到取完所有的红色像素,接着最后是255、134、…、255、134等等,直到得到一个特征向量,把图片中所有的红、绿、蓝像素值都列出来。(可以想象成把所有画素值并成一列或者一排,这里最好理解成一列,因为后续的思路是按列来看的),如果图片的大小为64x64像素,那么向量 x 的总维度,将是64乘以64乘以3,这是三个像素矩阵中像素的总量。
为了把这些像素值放到一个特征向量(这个是重点,特征向量!这个是后面很多神经网络的核心思维!)中,我们需要把这些像素值提取出来,然后放入一个特征向量x。为了把这些像素值转换为特征向量 x,我们需要像下面这样定义一个特征向量 x 来表示这张图片,我们把所有的像素都取出来,例如255、231等等,直到取完所有的红色像素,接着最后是255、134、…、255、134等等,直到得到一个特征向量,把图片中所有的红、绿、蓝像素值都列出来。(可以想象成把所有画素值并成一列或者一排,这里最好理解成一列,因为后续的思路是按列来看的),如果图片的大小为64x64像素,那么向量 x 的总维度,将是64乘以64乘以3,这是三个像素矩阵中像素的总量。
在这个例子中结果为12,288。现在我们用n_x=12,288,来表示输入特征向量的维度,有时候为了简洁,我会直接用小写的n来表示输入特征向量x的维度。所以在二分类问题中,我们的目标就是习得一个分类器,它以图片的特征向量作为输入,然后预测输出结果y为1还是0,也就是预测图片中是否有猫:
符号定义 :
x:表示一个n_x维数据,为输入数据,维度为(n_x,1);
y:表示输出结果,取值为(0,1)(取值问题,一定要注意,这个是后期输出值的把控重点!);
(x(i),y(i))(代表x的(i)上标,y的(i)上标):表示第i组数据,可能是训练数据,也可能是测试数据,此处默认为训练数据;
X=[x(1),x(2),…,x^(m)]:表示所有的训练数据集的输入值,放在一个 n_x×m的矩阵中,其中m表示样本数目;
Y=[y(1),y(2),…,y^(m)]:对应表示所有训练数据集的输出值,维度为1×m。
此处方便理解,特意截图出来,希望能了解!

用一对(x,y)来表示一个单独的样本,x代表n_x维的特征向量,y 表示标签(输出结果)只能为0或1。 而训练集将由m个训练样本组成,其中(x(1),y(1))表示第一个样本的输入和输出,(x(2),y(2))表示第二个样本的输入和输出,直到最后一个样本(x(m),y(m)),然后所有的这些一起表示整个训练集。有时候为了强调这是训练样本的个数,会写作M_train,当涉及到测试集的时候,我们会使用M_test来表示测试集的样本数,所以这是测试集的样本数:

最后为了能把训练集表示得更紧凑一点,我们会定义一个矩阵用大写X的表示,它由输入向量x(1)、x(2)等组成,如下图放在矩阵的列中,所以现在我们把x(1)作为第一列放在矩阵中,x(2)作为第二列,x(m)放到第m列,然后我们就得到了训练集矩阵X。所以这个矩阵有m列,m是训练集的样本数量,然后这个矩阵的高度记为n_x,注意有时候可能因为其他某些原因,矩阵X会由训练样本按照行堆叠起来而不是列,如下图所示:x(1)的转置直到x^(m)的转置,但是在实现神经网络的时候,使用左边的这种形式,会让整个实现的过程变得更加简单
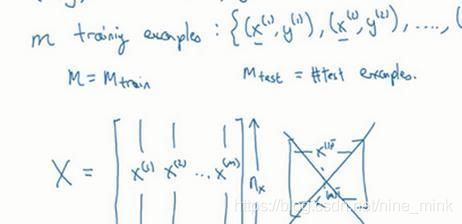
现在来简单温习一下:X是一个规模为n_x乘以m的矩阵,当你用Python实现的时候,你会看到X.shape,这是一条Python命令,用于显示矩阵的规模,即X.shape等于(n_x,m),X是一个规模为n_x乘以m的矩阵。所以综上所述,这就是如何将训练样本(输入向量X的集合)表示为一个矩阵。
那么输出标签y呢?同样的道理,为了能更加容易地实现一个神经网络,将标签y放在列中将会使得后续计算非常方便,所以我们定义大写的Y等于y(1),y(m),…,y^(m),所以在这里是一个规模为1乘以m的矩阵,同样地使用Python将表示为Y.shape等于(1,m),表示这是一个规模为1乘以m的矩阵。
 当你在后面的课程中实现神经网络的时候,你会发现,一个好的符号约定能够将不同训练样本的数据很好地组织起来。而所说的数据不仅包括 x 或者 y 还包括之后你会看到的其他的量。
当你在后面的课程中实现神经网络的时候,你会发现,一个好的符号约定能够将不同训练样本的数据很好地组织起来。而所说的数据不仅包括 x 或者 y 还包括之后你会看到的其他的量。
将不同的训练样本的数据提取出来,然后就像刚刚我们对 x 或者 y 所做的那样,将他们堆叠在矩阵的列中,形成我们之后会在逻辑回归和神经网络上要用到的符号表示。