24考研数学每日一题(带解析)
题目来源于武老师的每日一题,答案是自己做的,不太严谨,仅供参考

2022年11月1日
知识点:函数定义域
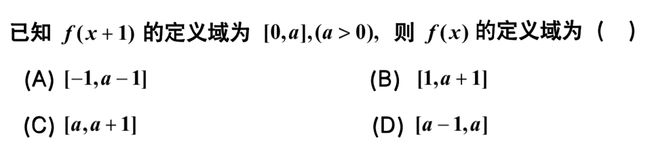
答案:
函数定义域是指自变量 x 的取值范围,不可以把 x + 1 作为自变量, x 才是自变量, 同一个 f ( ) ,括号内整体范围相同。由题意得 0 ⩽ x ⩽ a ⇒ 1 ⩽ x + 1 ⩽ a + 1 ,所以 f ( x ) 定义域为 [ 1 , a + 1 ] \text{函数定义域是指自变量}x\text{的取值范围,不可以把}x+1\text{作为自变量,}x\text{才是自变量,} \\ \text{同一个}f()\text{,括号内整体范围相同。由题意得}0\leqslant x\leqslant a\Rightarrow 1\leqslant x+1\leqslant a+1\text{,所以}f\left( x \right) \text{定义域为}\left[ 1,a+1 \right] 函数定义域是指自变量x的取值范围,不可以把x+1作为自变量,x才是自变量,同一个f(),括号内整体范围相同。由题意得0⩽x⩽a⇒1⩽x+1⩽a+1,所以f(x)定义域为[1,a+1]
2022年11月2日
知识点:函数定义域

答案:
f [ φ ( x ) ] = 1 − x 2 , f ( x ) = e x 2 ⟹ e φ 2 ( x ) = 1 − x , 两边同时求 ln , φ 2 ( x ) = ln ( 1 − x ) 由题意得 φ ( x ) ≥ 0 , 两边开根号 , φ ( x ) = ln ( 1 − x ) , 负半边不要了,只留正的。定义域: ln ( 1 − x ) ≥ 0 ⇒ 1 − x ≥ 1 ⇒ x ≤ 0 f\left[ \varphi \left( x \right) \right] =1-x^2,f\left( x \right) ={e^x}^{^2}\Longrightarrow e^{\varphi ^2\left( x \right)}=1-x,\text{两边同时求}\ln ,\varphi ^2\left( x \right) =\ln \left( 1-x \right) \\ \text{由题意得}\varphi \left( x \right) \ge 0,\text{两边开根号},\varphi \left( x \right) =\sqrt{\ln \left( 1-x \right)},\text{负半边不要了,只留正的。定义域:}\ln \left( 1-x \right) \ge 0\Rightarrow 1-x\ge 1\Rightarrow x\le 0 f[φ(x)]=1−x2,f(x)=ex2⟹eφ2(x)=1−x,两边同时求ln,φ2(x)=ln(1−x)由题意得φ(x)≥0,两边开根号,φ(x)=ln(1−x),负半边不要了,只留正的。定义域:ln(1−x)≥0⇒1−x≥1⇒x≤0
2022年11月3日
知识点:复合函数
g ( x ) = { 2 − x , x ≤ 0 x + 2 , x ≥ 0 , f ( x ) = { x 2 , x < 0 − x , x ≥ 0 , f ( x ) 是 g ( x ) 的复合函数 x 2 , x < 0 但是 x 2 > 0 , − x , x ≥ 0 但是 − x < 0 , 所以 g [ f ( x ) ] = { 2 + x , x ≥ 0 x 2 + 2 , x < 0 , 注意 x 的取值,与 f ( x ) 的取值是一致的 g\left( x \right) =\begin{cases} 2-x, x\le 0\\ x+2,x\ge 0\\ \end{cases},f\left( x \right) =\begin{cases} x^2, x<0\\ -x,x\ge 0\\ \end{cases},f\left( x \right) \text{是}g\left( x \right) \text{的复合函数} \\ x^2,x<0\text{但是}x^2>0,-x,x\ge 0\text{但是}-x<0,\text{所以}g\left[ f\left( x \right) \right] =\begin{cases} 2+x^{}, x\ge 0\\ x^2+2,x<0\\ \end{cases},\text{注意}x\text{的取值,与}f\left( x \right) \text{的取值是一致的} g(x)={2−x,x≤0x+2,x≥0,f(x)={x2,x<0−x,x≥0,f(x)是g(x)的复合函数x2,x<0但是x2>0,−x,x≥0但是−x<0,所以g[f(x)]={2+x,x≥0x2+2,x<0,注意x的取值,与f(x)的取值是一致的
2022年11月4日
知识点:反函数
把 f ( x ) 分段拆开来看 , 当 x < − 1 , y = 1 − 2 x 2 ⇒ x = ± 1 − y 2 , 因为 x < − 1 , x = − 1 − y 2 , x = − 1 时 , y = − 1 , 所以 x = − 1 − y 2 , y < − 1 。 当 − 1 ≤ x ≤ 2 时 , y = x 3 ⇒ x = y 3 , 当 x = − 1 时 , y = − 1 , 当 x = 2 时 , y = 8 所以 x = y 3 , − 1 ≤ y ≤ 8 。 当 x > 2 时 , y = 12 x − 16 ⇒ x = y + 16 12 , x = 2 , y = 8 , 所以 x = y + 16 12 , y > 8 。 把 y 换成 x , g ( x ) = { − 1 − x 2 , x < − 1 x 3 , − 1 ≤ x ≤ 8 x + 16 12 , x > 8 \text{把}f\left( x \right) \text{分段拆开来看},\text{当}x<-1,y=1-2x^2\Rightarrow x=\pm \sqrt{\frac{1-y}{2}},\text{因为}x<-1,x=-\sqrt{\frac{1-y}{2}},x=-1\text{时},y=-1,\text{所以}x=-\sqrt{\frac{1-y}{2}},y<-1\text{。} \\ \text{当}-1\le x\le 2\text{时},y=x^3\Rightarrow x=\sqrt[3]{y},\text{当}x=-1\text{时},y=-1,\text{当}x=2\text{时},y=8\text{所以}x=\sqrt[3]{y},-1\le y\le 8\text{。} \\ \text{当}x>2\text{时},y=12x-16\Rightarrow x=\frac{y+16}{12},x=2,y=8,\text{所以}x=\frac{y+16}{12},y>8\text{。} \\ \text{把}y\text{换成}x,g\left( x \right) =\left\{ \begin{array}{c} -\sqrt{\frac{1-x}{2}},x<-1\\ \sqrt[3]{x},-1\le x\le 8\\ \frac{x+16}{12},x>8\\ \end{array} \right. 把f(x)分段拆开来看,当x<−1,y=1−2x2⇒x=±21−y,因为x<−1,x=−21−y,x=−1时,y=−1,所以x=−21−y,y<−1。当−1≤x≤2时,y=x3⇒x=3y,当x=−1时,y=−1,当x=2时,y=8所以x=3y,−1≤y≤8。当x>2时,y=12x−16⇒x=12y+16,x=2,y=8,所以x=12y+16,y>8。把y换成x,g(x)=⎩ ⎨ ⎧−21−x,x<−13x,−1≤x≤812x+16,x>8
2022年11月5日
知识点:函数奇偶性
重点
设 h ( x ) 为奇函数, g ( x ) 为偶函数可以使 f ( x ) = h ( x ) + g ( x ) 成立, h ( − x ) = − h ( x ) , g ( − x ) = g ( x ) f ( − x ) = h ( − x ) + g ( − x ) = − h ( x ) + g ( x ) , { f ( x ) = h ( x ) + g ( x ) f ( − x ) = − h ( x ) + g ( x ) ⇒ g ( x ) = 1 2 [ f ( x ) + f ( − x ) ] ( x 与 − x 互换等式结果一样,偶函数 ) , h ( x ) = 1 2 [ f ( x ) − f ( − x ) ] ( x 与 − x 互换等式结果一样,奇函数 ) \text{设}h\left( x \right) \text{为奇函数,}g\left( x \right) \text{为偶函数可以使}f\left( x \right) =h\left( x \right) +g\left( x \right) \text{成立,}h\left( -x \right) =-h\left( x \right) ,g\left( -x \right) =g\left( x \right) \\ f\left( -x \right) =h\left( -x \right) +g\left( -x \right) =-h\left( x \right) +g\left( x \right) ,\left\{ \begin{array}{c} f\left( x \right) =h\left( x \right) +g\left( x \right)\\ f\left( -x \right) =-h\left( x \right) +g\left( x \right)\\ \end{array}\Rightarrow g\left( x \right) =\frac{1}{2}\left[ f\left( x \right) +f\left( -x \right) \right] \left( x\text{与}-x\text{互换等式结果一样,偶函数} \right) ,h\left( x \right) =\frac{1}{2}\left[ f\left( x \right) -f\left( -x \right) \right] \left( x\text{与}-x\text{互换等式结果一样,奇函数} \right) \right. 设h(x)为奇函数,g(x)为偶函数可以使f(x)=h(x)+g(x)成立,h(−x)=−h(x),g(−x)=g(x)f(−x)=h(−x)+g(−x)=−h(x)+g(x),{f(x)=h(x)+g(x)f(−x)=−h(x)+g(x)⇒g(x)=21[f(x)+f(−x)](x与−x互换等式结果一样,偶函数),h(x)=21[f(x)−f(−x)](x与−x互换等式结果一样,奇函数)
2022年11月6日
知识点:函数基本性质
f ( − x ) = − x tan ( − x ) ⋅ e sin − x = x tan x ⋅ e − sin x , f ( x ) ≠ f ( x ) , A 错 e sin x 为周期函数, tan x 为周期函数, x 单调递增,相乘后不是周期函数, C 错 x , tan x 在 ( − π 2 , π 2 ) 上单调递增, e sin x 为周期函数,则 f ( x ) 不是单调函数, D 错,证明出 B 正确 f\left( -x \right) =-x\tan \left( -x \right) \cdot e^{\sin -x}=x\tan x\cdot e^{-\sin x},f\left( x \right) \ne f\left( x \right) ,A\text{错} \\ e^{\sin x}\text{为周期函数,}\tan x\text{为周期函数,}x\text{单调递增,相乘后不是周期函数,}C\text{错} \\ x,\tan x\text{在}\left( -\frac{\pi}{2},\frac{\pi}{2} \right) \text{上单调递增,}e^{\sin x}\text{为周期函数,则}f\left( x \right) \text{不是单调函数,}D\text{错,证明出}B\text{正确} f(−x)=−xtan(−x)⋅esin−x=xtanx⋅e−sinx,f(x)=f(x),A错esinx为周期函数,tanx为周期函数,x单调递增,相乘后不是周期函数,C错x,tanx在(−2π,2π)上单调递增,esinx为周期函数,则f(x)不是单调函数,D错,证明出B正确