【从FT到DFT和FFT】（三）从离散傅里叶变换到快速傅里叶变换

推荐阅读

前置阅读

1. 【从FT到DFT和FFT】（一）从三角函数正交性到傅里叶变换的详细公式推导_Twilight Sparkle.的博客-CSDN博客
2. 【从FT到DFT和FFT】（二）从傅里叶变换到离散傅里叶变换_Twilight Sparkle.的博客-CSDN博客

推荐阅读

• From FFT to NTT | fat fatzard’s Blog
• 【数字信号处理】【傅里叶分析】【FFT】快速傅里叶变换的完整公式推导_寒霜雨刃的博客-CSDN博客
• 十分简明易懂的FFT（快速傅里叶变换）_路人黑的纸巾的博客-CSDN博客_fft

前言

早在打ACM时对FFT就有所耳闻，学长一再叮嘱一定要每个队员都把FFT尽早学会。当时只知道FFT可以拿来加速多项式乘法，可以将时间复杂度从$O(n^2)$加速至$O(nlogn)$ 。奈何我是数论fw，一直迟迟没有学习。直到图像处理，才知道FFT其实是离散傅里叶变换（DFT）的加速版，多项式乘法不过是它的应用之一。

我查到的推导FFT的过程大多都是从多项式乘法入手，在这里先贴上我某数论朋友的FFT详细推导（推荐阅读第一篇文章），他在文章中同时用代码详细实现了FFT，并且进一步推导了快速数论变换（NTT），如果对公式推导和代码实现感兴趣的朋友，强力推荐。

从离散傅里叶变换到快速傅里叶变换

上篇提到的离散傅里叶变换(DFT)公式以及逆变换公式：
$$\begin{array}{rl}& X[k]=\sum _{m=0}^{M-1}x[m]e^{-i\frac{2\pi }{M}mk}\\ & x[k]=\frac{1}{M}\sum _{m=0}^{M-1}X[m]e^{i\frac{2\pi }{M}mk}\end{array}$$
我们先讨论正变换公式：
$$X[k]=\sum _{m=0}^{M-1}x[m]e^{-i\frac{2\pi }{M}mk}$$
现在考虑来对一个长度为N的离散非周期序列做离散傅里叶变换，时间复杂度很容易看出是$O(n^2)$。接下来我们将使用FFT把时间复杂度减小到$O(nlogn)$。

单位根

复数$w$满足$w^n=1$ 称作w是n次单位根。如果你看过傅里叶变换原理，应该可以知道复数相乘其实是旋转。
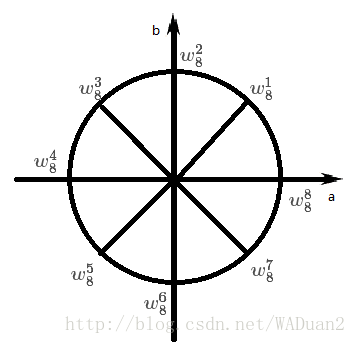
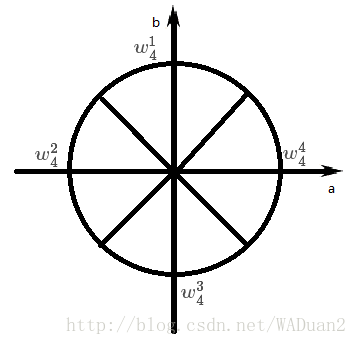
接下来例举8次单位根和4次单位根图像：

注：这两幅图来自博客：FFT算法讲解——麻麻我终于会FFT了！_Duan2baka的博客-CSDN博客_fft算法

能够轻易看出，
$$\begin{array}{rl}& w_{2n}^{2m}=w_n^m\\ & w_n^m=-w_n^{m+\frac{n}{2}}\end{array}$$

对DFT进行分治得到FFT

设多项式$A(x)$:
$$A(x)=\sum _{i=0}^{n-1}{a}_i{x}^i=a_0+a_{1}x+a_2{x}^2+...+a_{n-1}{x}^{n-1}$$

仔细观察DFT，其实$A(x)$ 就是DFT的简化版。

对$A(x)$根据奇偶性劈成两半：
$$\begin{array}{rl}A(x)& =(a_0+a_2{x}^2+...+a_{n-2}{x}^{n-2})+(a_{1}x+a_3{x}^3+...+a_{n-1}{x}^{n-1})\\ & =(a_0+a_2{x}^2+...+a_{n-2}{x}^{n-2})+x(a_1+a_3{x}^2+...+a_{n-1}{x}^{n-2})\end{array}$$
现在，设:
$$\begin{array}{rl}& A_1(x)=a_0+a_{2}x+a_4{x}^2+...+a_{n-2}{x}^{\frac{n}{2}-1}\\ & A_2(x)=a_1+a_{3}x+a_5{x}^2+...+a_{n-1}{x}^{\frac{n}{2}-1}\end{array}$$
于是：
$$A(x)=A_1(x^2)+x{A}_2(x^2)$$

计算前半截

设$k<\frac{n}{2}$，将$x$换为单位根$w_n^k$:
$$\begin{array}{rl}A(w_n^k)& =A_1(w_n^{2k})+w_n^k{A}_2(w_n^{2k})\\ & =A_1(w_{\frac{n}{2}}^k)+w_n^k{A}_2(w_{\frac{n}{2}}^k)\end{array}$$

计算后半截

将$w_n^{k+\frac{n}{2}}$ 代入$A(w_n^{k+\frac{n}{2}})$:
$$\begin{array}{rl}A(w_n^{k+\frac{n}{2}})& =A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}{A}_2(w_n^{2k+n})\\ & =A_1(w_n^{2k}{w}_n^n)-w_n^k{A}_2(w_n^{2k}{w}_n^n)\\ & =A_1(w_n^{2k})-w_n^k{A}_2(w_n^{2k})\\ & =A_1(w_{\frac{n}{2}}^k)-w_n^k{A}_2(w_{\frac{n}{2}}^k)\end{array}$$

---

我们发现前半截和后半截要计算的局部都一样，不过符号不一样。所以只需要计算$A_1(w_{\frac{n}{2}}^k)$ 、$A_2(w_{\frac{n}{2}}^k)$,就可以计算出前半段和后半段的值。所以我们可以利用分治：每次回溯只扫描前一半的序列，即可得后一半序列结果。时间复杂度自然缩短为$O(nlogn)$ 。对DFT进行分治的算法就叫FFT。

快速傅里叶逆变换（IFFT）

结论：一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数。

看不懂？这里解释一下这句话在说什么。

考虑这样一个问题：现在要将离散频域信号变为离散时域信号，即离散傅里叶逆变换（IDFT），现在需要利用分治加速（IFFT）。

前面已经提到了IDFT的公式：
$$x[k]=\frac{1}{M}\sum _{m=0}^{M-1}X[m]e^{i\frac{2\pi }{M}mk}$$
使用同样的思路，对${\sum }_{m=0}^{M-1}X[m]e^{i\frac{2\pi }{M}mk}$ 进行分治即可。

不过在分治过程中，观察DFT和IDFT指数部分的不同：

DFT：$e^{-i\frac{2\pi }{M}mk}$

IDFT:$e^{i\frac{2\pi }{M}mk}$

发现没，这两个虚部是相反数。所以对于FFT的分治步骤，需要对单位根乘共轭复数才是IFFT的分治步骤。

然后直接看公式就知道，分治结束了还要除个M。