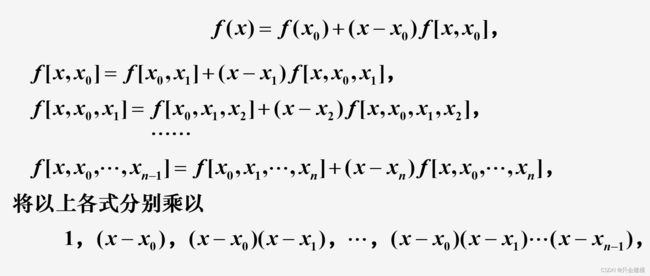数学建模及数据分析上的插值处理——第二部分实践线性插值及牛顿插值

2.分段线性插值

  实际工作中，并非插值多项式次数越高误差越小，常采用分段多项式插值。分段多项式插值就是求一个分段（共n段）多项式 P(x)，使其满足插值条件或更高要求。
  分段一次多项式插值y=f(x)，几何上就是用折线代替曲线 ，也称折线插值或分段线性插值。分段线性插值多项式P1(x)为

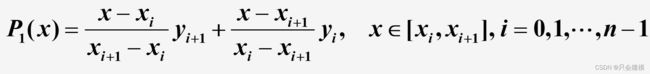
3.分段二次插值

  这里插值函数P2(x)是一个二次多项式，在几何上就是分段抛物线代替曲线y=f(x) ，也称分段抛物线插值，此时要求有2n+1个节点，其插值公式为

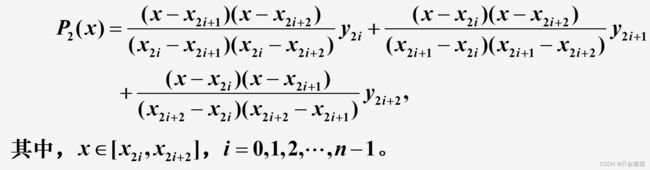
4.牛顿插值

  在导出Newton插值公式前，先介绍公式表示中所需要用到的差分和差商概念。

def diff_forward(f, k, h, x):
    if k<=0: return f(x)
    else: return diff_forward(f, k-1, h, x+h) - diff_forward(f, k-1, h, x)

"""计算n阶差商 f[x0, x1, x2 ... xn]
输入参数：xi为所有插值节点的数组
输入参数：fi为所有插值节点函数值的数组
返回值:  返回xi的i阶差商(i为xi长度减1)"""
def diff_quo(xi=[], fi=[]):
    if len(xi)>2 and len(fi)>2:
        return (diff_quo(xi[:len(xi)-1],fi[:len(fi)-1])-diff_quo(xi[1:len(xi)],fi[1:len(fi)]))\
                /float(xi[0]-xi[-1])  #续行
    return (fi[0]- fi[1])/float(xi[0]-xi[1])

5.样条插值

  许多工程技术中提出的计算问题对插值函数的光滑性有较高要求，如飞机的机翼外形，内燃机的进气门、排气门的凸轮曲线，都要求曲线不仅连续，而且具有连续的曲率，这即是样条函数提出的背景之一。

  样条（spline）本来是工程设计中的一种绘图工具，是富有弹性的细木条或细金属条，绘图员利用它把已知点连接成一条光滑曲线（称为样条曲线），并使连接点处有连续曲率。三次样条插值就是由此抽象出来的。

6.二维数据的双三次样条插值

  对于二维数据的插值，首先要考虑两个问题：一是二维区域是任意区域还是规则区域；二是给定的数据是有规律分布的还是散乱、随机分布的。
  第一个问题比较容易处理，只需将不规则区域划分为规则区域或扩充为规则区域来讨论即可。对于第二个问题，当给定的数据是有规律分布时，方法较多也较成熟；而给定的数据是散乱、随机分布时，没有固定的方法，但一般的处理思想是：从给定的数据出发，依据一定的规律恢复出规则分布点上的数据，转化为数据分布有规律的情形来处理。
  当给定的二维数据在规则区域上有规律分布时，一种常用的插值方法是所谓的双三次样条插值。其基本思想是，对于给定未知函数z=f(x,y)的二维观测数据如下表所示。它们对x轴和y轴的分割：

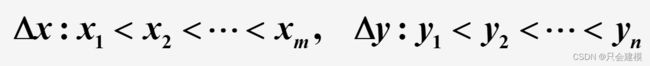
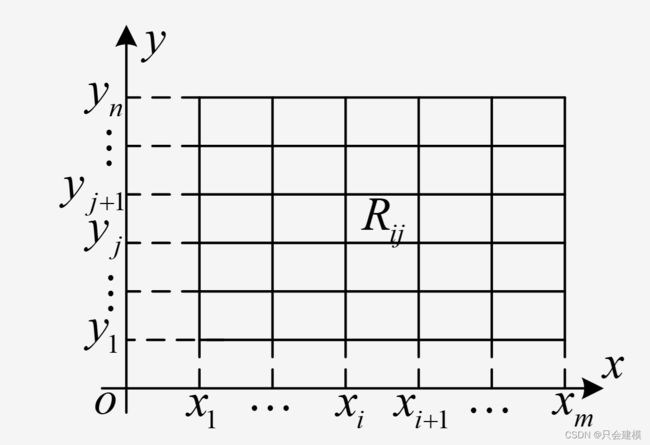
  可以导出xy平面上矩形区域R的一个矩形网格分割 ，如下图所示。

  scipy.interpolate模块有一维插值函数interp1d，二维插值函数interp2d，多维插值函数interpn、interpnd。
  interp1d的基本调用格式为
  interp1d(x, y, kind=‘linear’)
  其中kind的取值是字符串，指明插值方法，kind的取值可以为：‘linear’, ‘nearest’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’等，这里的’zero’, ‘slinear’, ‘quadratic’ and 'cubic’分别指的是0阶、1阶、2阶和3阶样条插值。

1.一维插值

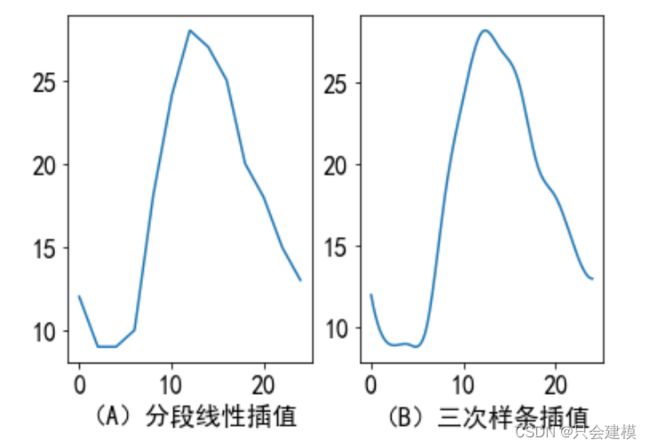
  例 在一天24小时内，从零点开始每间隔2小时测得的环境温度（摄氏度）如下表所示。分别进行分段线性插值和三次样条插值，并画出插值曲线。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d 
x=np.arange(0,25,2)
y=np.array([12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13])
xnew=np.linspace(0, 24, 500)  
#插值点
f1=interp1d(x, y); y1=f1(xnew);
f2=interp1d(x, y,'cubic'); y2=f2(xnew)
plt.rc('font',size=16); plt.rc('font',family='SimHei')
plt.subplot(121), plt.plot(xnew, y1); plt.xlabel("（A）分段线性插值")
plt.subplot(122); plt.plot(xnew, y2); plt.xlabel("（B）三次样条插值")
plt.savefig("figure7_4.png", dpi=500)
plt.show()