插头DP && 概率DP / 期望DP
插头DP && 概率DP / 期望DP
-
- 写在前面:
- 插头DP
-
- P5056 【模板】插头dp
-
- 手写哈希表的方法:
- 拉链法的代码如下:
- 开放寻址法的代码如下:
- 接下来是这道题的代码实现:
- P3190 [HNOI2007]神奇游乐园
-
- 具体的代码实现如下:
- P3272 [SCOI2011]地板
-
- 具体的代码实现如下:
- 期望DP
-
- UVA12230 过河 Crossing Rivers
-
- 具体的代码实现如下:
- 期望dp / 概率dp的概念:
- 期望DP / 概率DP常见的状态表示及其转移:
- SP1026 FAVDICE - Favorite Dice
-
- 具体的代码实现如下:
- 【SGU495】【Kids and Prizes】
-
- 具体的代码实现如下:
- CF148D Bag of mice
-
- 具体的代码实现如下:
- POJ 3071 Football
-
- 具体的代码实现如下:
- CodeForces 768 D - Jon and Orbs
-
- 具体的代码实现如下:
- POJ2096 Collecting Bugs
-
- 具体的代码实现如下:
- P1850 [NOIP2016 提高组] 换教室
-
- 具体的代码实现如下:
- HDU3853 LOOPS
-
- 具体的代码实现如下:
- 总结:
写在前面:
快开学了,先发下最近整理的DP,还有过年前学的状压DP、记忆化搜索等基础DP还有图论等知识还在整理中…
由于本人平时比较懒,所以把十几道题都弄在一篇博客,这篇博客比较长,近3万字,但我相信大家还是能看懂我在说什么的。
插头DP
P5056 【模板】插头dp
有些状压DP问题要求我们记录状态的连通性信息,这类问题一般被形象的称为插头DP或连通性状态压缩DP。插头dp是基于连通性状态压缩的动态规划,一般的适用范围:数据范围小,并且处于网格图中,对连通性有要求(要求选择出来的格子是一个连通块或者是一个路径/回路)。这样说起来很抽象,我先介绍一道插头dp的模板题:
给我们一个n * m的棋盘,这个棋盘里面有些格子是障碍,有些格子是空格,求这个棋盘有多少个不同的哈密顿回路(要经过每个格子,并且每个格子只能经过一遍),我们来简单回顾一下哈密顿回路的做法:先用一个状态S表示我们当前已经走过哪些点,另外用i表示我们当前走到了哪个点,然后枚举下一个点是哪一个点,假设下一个点是j,f(s, i)就变成了f(s | 1 << j, j),此时的时间复杂度是2n * n2,现在是一个棋盘,如果按照这种做法来做时间复杂度会太大。棋盘有个特点:每个格子只能和上下左右四个格子相连,并不是能和任意格子相连,所以可以按照一行一行来枚举所有状态(对于一般图我们就不能这样),我们递推的时候一般是按格来递推,举个例子,我们要考虑这个格子,这也意味着我们已经考虑完了这个红色线上方的格子,所以此时我们只要分析这个格子的状态就可以了。

因为我们要组成一个回路,所以每个格子只能有两条边会被经过,假设有一个边是进来的,有一个边是出去的,也就是在它的四条边里边选两条边经过,这样经过每个格子有6种情况,对于整一个连通块,我们只关心它轮廓线上的状态(即每条边有没有线经过),还要维护轮廓线上方部分的连通性(经过轮廓线的边哪些是属于同个连通块的)

(上面0和7,3和6就是属于同一个连通块)记录连通块一般有两种方法:1、最小表示法,从左往右遍历轮廓线,当遍历到没被标记的边(且有路径要经过它)的时候,按顺序标记,所以0和7标记成1,3和6标记成2(属于同个连通块标记相同),所以此时轮廓线的状态:10020021。2、括号表示法,括号表示法的适用范围要小一些,但效率更高(首选),因为我们要找的是一个哈密顿回路,这就意味着上半部分有一条边上去,就一定有一条边下来,这些边必然是两两配对的,而且这两条边之间的连通块是不可能交叉的(两条边所连的路径不可能交叉),因为是相邻的两两配对,所以可以看做是若干个括号,我们用1表示“左括号”,用2表示有括号,用一个三进制的数就能表示轮廓线的状态,所以此时轮廓线的状态:10010022。
这道题用括号表示法比用最小表示法的优势是,我们用012就可以表示轮廓线的状态,而最小表示法要用到的数可能很大(有多少个连通块,最大就是多少)。另外,括号表示法每一位就012,可以把它看成是4进制,然后在更新状态的时候就可以用位运算去优化。
状态表示是三维,f[i, j, s]表示当遍历到第i行第j列的格子的时候分界线的状态是s时,所有方案的数量,s有效的状态是4、5万个(因为它要满足1和2是两两配对的)。插头dp比较麻烦的就是状态转移,我们把目标格子(g[i, j])在轮廓线上的边标记成x和y,轮廓线上的状态为state,需要分成以下几种情况(转移的过程中x对应格子下面的边,y对应格子右边的边):
1、g[i, j]是障碍物,x和y一定是0,且这个格子也不会有路径经过,所以state不变(x和y都是0,转移之后也是0)
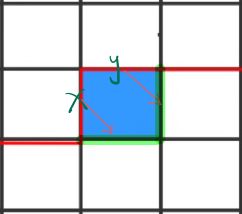
接下来g[i, j]不是障碍物的情况:
2、x和y均为0,更新后state中x = 1, y = 2

3、x为0,y非0,更新后state中状态不变或者x = y, y = 0


4、x非0,y为0,更新后state中y = x, x = 0或者状态不变
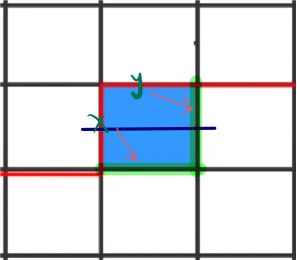
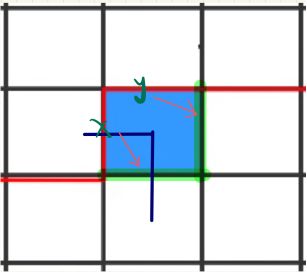
5、x = y = 1,x和y相连,此时state中原来x和y的位置变成0,然后离y最近的2变成1,又因为格子已经有两条边了,所以更新之后x和y对应的位置为0。

6、x = y = 2,x和y相连,此时state中原来x和y的位置变成0,然后离x最近的1变成2,又因为格子已经有两条边了,所以更新之后x和y对应的位置为0。
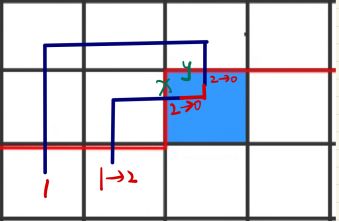
7、x = 2, y = 1,x与其前面第一个1配对,y与后面第一个2配对,更新后state中x = 0, y = 0。
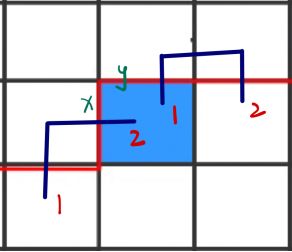
8、x = 1, y = 2,x是某个路径的左半边,y是某个路径的右半边,又因为x和y在轮廓线中是相邻的,所以x和y是属于同一个路径的,这种情况只会发生在最后一个合法的格子。
接下来分析数据,在f[i, j, s]中s是轮廓线的状态,因为我们是用四进制来表示三进制,而4的13次方是等于67108864,而有效的状态只有4w多个,所以插头dp在存状态的时候一般是用哈希表来存的,而且哈希表最好不要用stl中的哈希表,因为插头dp的常数比较大,题目卡得比较严,所以现在我们要手写哈希表…
手写哈希表的方法:
1、开放寻址法
2、拉链法
哈希表的作用:从较庞大的空间/值域,把它映射到一个较小的空间(0 ~ N)。
结合这道题来介绍手写哈希表的两种做法:

当要存储的数是x时,我们可以构造一个哈希函数h(x),这个函数它可以把-109 ~ 109的一个数映射到0 ~ 105之间的一个数,通常会采取x % 105的做法,值域比较大,但是映射的结果比较小,所以必然会产生冲突,也就是我们可能会把两个相同的数映射成同一个数,对于冲突的解决方式可以采用两种方法(开放寻址法/拉链法)。
拉链法:
先开一个长度为105的数组,当两个数发生冲突的时候,就在某个位置i拉下一条链,把之前的数放在链的第一个位置,然后把新得到的数放在i位置,类似于对于某一个数组元素接一个邻接表。哈希算法是一种期望算法,虽然说每一个位置都有可能拉下来一条链,但是在平均情况下,每一条链的长度可以看成是常数,所以哈希表的时间复杂度可以看成O(1)。
我们在建立一个哈希表的长度的时候一般取成一个质数(就是取模的数),而且这个质数要离2的n次方尽可能远。定义h[N]哈希数组,对于每一个“槽”,我们要向下拉一条链(类似于之前的链表),链表要存两个东西,一个是它的值e[idx],另一个是下一个值的下标ne[idx],具体做法和对链表的插入查找相同。
拉链法的代码如下:
const int N = 100003;
int h[N], e[N], ne[N], idx;
int insert(int x){
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx++;
}
int find(int x){
int k = (x % N + N) % N;
for(int i = h[k]; i != -1; i = ne[i]){
if(e[i] == x) return 1;
}
return 0;
}
int main(){
int n, m;
cin >> n;
char p[2];
memset(h, -1, sizeof(h));
while(n--){
scanf("%s%d", p, &m);
if(p[0] == 'I') insert(m);
else{
if(find(m)) cout << "Yes\n";
else cout << "No\n";
}
}
return 0;
}
开放寻址法:
它只开了一个一维数组,一维数组的长度一般要开到题目数据范围的两到三倍(这道题开到20w ~ 30w),这样的话冲突的概率就小一点。开放寻址法就像我们去厕所找坑位,我想要的坑位有人了,就按顺序看看下一个空位有没有人,以此类推,直到找到坑位为止。
开放寻址法的代码如下:
const int N = 200003, null = 0x3f3f3f3f;
int find(int x){
int k = (x % N + N) % N;
while(h[k] != null && h[k] != x){
k++;
if(k == N) k = 0;
}
return k;
}
int main(){
int n, m;
cin >> n;
char p[2];
memset(h, 0x3f, sizeof(h));
while(n--){
scanf("%s%d", p, &m);
if(p[0] == 'I') h[find(m)] = m;
else{
if(h[find(m)] == null) cout << "No\n";
else cout << "Yes\n";
}
}
return 0;
}
言归正传,我在插头dp这道题用开放寻址法,另外,这个题目合法状态大约4w多个,估算一下5w * 144(格子数),大概是700多w个状态,有些题目的数量可能更多,所以要用到滚动数组。由于对于每个格子,总共的状态有6k多w个,合法状态只有不到5w个,我们去枚举的时候就没必要去枚举所有状态,而要用一个数组先存储每一次滚动的有效状态。估算下时间复杂度:f[i, j, s]假设所有有效状态数量是S(最多不到5w),再乘以i、j(n2),然后再算状态的时候,对于5和6的情况,我们是需要枚举找出与某条边配对的边,最坏情况下是需要O(N)的计算量,所以整个算法的时间复杂度就是S * n3,大概是5w * 12 * 12 * 12 = 8.64 * 107,但本质上来说没有这么高(有效状态不到5w,也不是所有状态都要枚举8种情况),这就是插头dp的具体思路。
接下来是这道题的代码实现:
(具体有点复杂,为了大家方便理解,我每一行我都加了注释,虽然我自己都觉得有点恶心…)
#include P3190 [HNOI2007]神奇游乐园
这道题相当于一个n * m的棋盘,然后从里边选择一个回路,但这道题跟上一题不一样的地方是不一定每一个格子都要经过,回路里边包含的格子数量不能少于四,也就是起码要存在一个拐点。要我们求在所有的回路里权值和最大是多少,状态表示和上面那道题是类似的,只有状态转移不太一样,我们用f[i, j, S]遍历到当前第i行j列的格子轮廓线的状态是S时所有方案的集合,S在存插头状态的时候,跟上面那道题是类似的,也是用三进制(类似于括号序列的方式)来存下每条边的状态,主要是维护下所有插头的连通性。
状态转移是7种情况(上一道题格子可能是障碍物),我就不画图了,用文字说明(每个变量表示的东西都跟上一道题一样):
情况一:x = 0, y = 0, 这个格子有两种可能(因为这个格子可以走,可以不走),不走的话,insert(cur, state, w);;走的话,insert(cur, state + set(j - 1, 1) + set(j, 2), w + g[i][j]);
情况二:x = 0, y非0,经过这个格子的时候如果向右走,insert(cur, state, w + g[i][j]);
如果向下走,insert(cur, state + set(j - 1, y) - set(j, y), w + g[i][j]);
情况三:x非0, y = 0,经过这个格子的时候如果向右走,insert(cur, state + set(j, x) - set(j - 1, x), w + g[i][j]);如果向下走,insert(cur, state, w + g[i][j]);
情况四:如果x = 1, y = 1,在y的右边找到第一个2与y配对,把其更新为1,insert(cur, state -set(j - 1, 1) - set(j, 1) - set(u, 1), w + g[i][j]);
情况五:如果x = 2, y = 2,在x的左边找到第一个1与x配对,把其更新为2,insert(cur, state - set(j - 1, 2) - set(j, 2) + set(u, 1), w + g[i][j]);
情况六:x = 2, y = 1,这种状态其它边不受影响,直接转移就好了insert(cur, state - set(j - 1, 2) - set(j, 1), w + g[i][j]);
情况七:x = 1, y = 2,这种状态说明轮廓线的上方已经形成了回路,因为这道题不是所有的格子都要走,所以当遇到这种情况的时候,我们要更新权值和的最大值:ans = max(ans, w + g[i][j]);
具体的代码实现如下:
(跟第一道题很像,只是状态转移的条件和过程不一样,其他辅助函数都一样)
#include P3272 [SCOI2011]地板
这道题是一个非回路的问题,在r * c的地面上铺地板,地面上可能有障碍物,没有障碍物的地方一定要铺上地板,而且铺的地板要呈”L”型(如题目图示),求铺满整个地面的总方案数。题目中r和c没有大小关系,但规定了r * c <= 100,因此r和c的最小值一定是小于等于10,从数据范围上看它也是可以用插头dp的,这一题跟上两道题不一样,它不是一个回路,就不可以用类似括号序列的方式来表示轮廓线的状态,这道题依旧用f[i, j, S]来表示遍历到第i行第j列的格子,轮廓线的状态是S时的方案数。这道题轮廓线上的插头状态
存的是”L”型地板经过轮廓线上的某一条边时,在轮廓线上方是否已经“拐弯”,它存的是每个插头当前有没有“拐弯”,如果无插头,记录为0;如果有插头且还没“拐弯”,记录为1;如果有插头且已经“拐弯”,记录为2。重点是如何进行状态转移,可以分成7种情况((每个变量表示的东西都跟上一道题一样):
情况一:如果这个格子是障碍物,insert(cur, state, w);
情况二:当格子不是障碍物时(下面的情况都是格子不是障碍物的情况),x = 0, y = 0,还可以分成三种子情况,以当前格子为起点,如果只往下走,insert(cur, state + set(j - 1, 1), w);如果只往右走,insert(cur, state + set(j, 1), w);如果既往下又往右走,insert(cur, state + set(j - 1, 2) + set(j, 2), w);
情况三:x = 0, y = 1,如果往下走,insert(cur, state + set(j - 1, 1) - set(j, 1), w);如果往右走insert(cur, state + set(j, 1), w);
情况四:x = 0, y = 2,如果往下走,insert(cur, state - set(j, 2) + set(j - 1, 2), w);如果在当前格子停下insert(cur, state - set(j, 2), w);如果已经遍历到最后一个有效格子,更新方案数,ans = (ans + w) % mod;
情况五:x = 1, y = 0,如果往右走,insert(cur, state - set(j - 1, 1) + set(j , 1) ,w);如果往下走,insert(cur, state + set(j - 1, 1), w);
情况六:x = 2, y = 0,如果往右走,insert(cur, state - set(j - 1, 2) + set(j , 2), w);如果在当前格子停下insert(cur, state - set(j - 1, 2), w);如果已经遍历到最后一个有效格子,更新方案数,ans = (ans + w) % mod;
情况七:x = 1, y = 1,这种情况说明这个格子是某个“L”型地板的“拐弯”处,insert(cur, state - set(j - 1, 1) - set(j, 1), w);如果此时已经遍历到了最后一个有效的格子,更新方案数,ans = (ans + w) % mod;
注意,这道题在进行状态转移的时候要考虑当前“L”型地板覆盖的地方有没有障碍物。
具体的代码实现如下:
(跟前两道插头dp很像,只是状态转移的条件和过程不一样,其他辅助函数都一样)
#include 期望DP
在介绍期望dp之前,先做一道简单的数学求期望,熟悉一下算法题是怎样考查期望的。
UVA12230 过河 Crossing Rivers

题意:从A到B需要经过n条河,已知AB间距离D和每条河的长度L以及在该条河上的船速v,求A到B平均情况下需多长时间。
陆地行走速度为1,船的位置和朝向均匀随机。因为在某条河里面船的位置和朝向是均匀随机的,人在河边最久等待2 * l / v(人到河边,船刚走),最理想情况是不用等待,所以平均等待时间的期望就是l / v,加上人坐船过河需要时间,所以人过河(包括等船)需要时间的期望为2 * l / v,一直人在陆地上的速度为1,所以每遇到河时,需要的期望时间就是在总路程长度中,减去河的长度(- l),再加上人过这条河需要时间的期望(+ 2 * l / v)。
具体的代码实现如下:
#include 期望dp / 概率dp的概念:
根据概率分析,递推求出每个状态的期望的算法。
期望DP / 概率DP常见的状态表示及其转移:
1、设成dp[i]表示已经完成i个,要达到目标状态的期望。也就是由i状态变成目标状态的期望。对于这种方法,转移的时候要选择刷表法倒序枚举。(根据这个状态本身就可以理解)
2、设成dp[i]表示已经完成i个的期望。对于这种方法,转移的时候要选择填表法正序枚举。
对于以上两种方法,很多时候可以互换。但是有些时候不能互换。需要经过具体情况灵活判断。
3、设成dp[i][j]表示i种物品选择了j个的期望。
4、设成dp[i][j]表示有i个第一种物品,j个第二种物品的期望。
对于以上两种方法,就是二维的状态转移。
然后就是转移的具体过程。对于状态转移,一般我们要把整个过程拆解成两种情况:已处理和未处理,也就是符合需要和不符合需要。比如抛硬币,要算正面朝上的期望,那么就把抛硬币的过程拆成:朝上和不朝上。或者掷一个有N面的骰子,要算掷多少次才能都掷完各面的期望,那么就把这个掷骰子的过程拆成:掷到已经处理的面和掷到未处理的面。
这样的话,就可以通过两种过程的概率以及上面所讲述的期望的性质进行转移。
对于填表、刷表法的选择:一般来讲,初始状态确定时用顺推填表,终止状态确定时可用逆推刷表。
SP1026 FAVDICE - Favorite Dice
一个n面的骰子,求期望掷几次能使得每一面都被掷到。dp[i]表示已经从n个面中掷出来i面后,掷出所有面的次数期望,所以dp[n] = 0, dp[0]即为所求。我们可以采用逆推刷表,已知在n面的骰子中已经掷出了i面,再掷一次恰好是没掷出的面的概率为(n - i) / n,所以从n面的骰子中掷出之前没掷出的面的期望次数是n / (n - i),因为是逆推刷表,所以状态转移方程:dp[i] = dp[i + 1] + n * 1.0 / (n - i); dp[0]即为所求的期望次数。
具体的代码实现如下:
#include 【SGU495】【Kids and Prizes】
这道题是我在网上找的期望dp的基础题,做完后想提交,才发现SGU这个oj没了…
题意:有n个奖品放在n个盒子里,有m个小朋友轮流去选择一个盒子,若有奖品则拿走,无论有没有奖品都要将空盒子放回去。问最后获得奖品个数的期望。
求获得奖品个数的期望,只要把每一个小朋友拿到奖品的概率相加即为所求,所以我们要dp求每一轮小朋友拿到奖品的概率,第一个小朋友拿到奖品的概率为1,dp[1] = 1;之后第i个小朋友拿到奖品的概率(dp[i])与第i - 1个小朋友拿到奖品(dp[i - 1])的概率有关,分为两种情况:当第i - 1个小朋友没有拿到奖品时,此时第i个小朋友拿到奖品的概率与第i - 1个小朋友拿到奖品的概率相同,此时dp[i] = (1 - dp[i - 1]) * dp[i -1];当第i - 1个小朋友拿到奖品时,第i个小朋友拿到奖品的概率是(dp[i - 1] - 1.0 / n),此时dp[i] = dp[i - 1] * (dp[i - 1] - 1.0 / n),结合起来,状态转移方程:dp[i] = (1 - dp[i - 1]) * dp[i - 1] + dp[i - 1] * (dp[i - 1] - 1 / n)。
具体的代码实现如下:
#include CF148D Bag of mice

cf的英文题,我大概说下题意:袋子里有 w 只白鼠和 b 只黑鼠,公主和龙轮流从袋子里抓老鼠。谁先抓到白色老鼠谁就赢,如果袋子里没有老鼠了并且没有谁抓到白色老鼠,那么算龙赢。公主每次抓一只老鼠,龙每次抓完一只老鼠之后会有一只老鼠跑出来。每次抓的老鼠和跑出来的老鼠都是随机的。公主先抓。问公主赢的概率。
设f[i, j]为轮到公主时袋子里有i只白鼠,j只黑鼠,公主赢的概率。初始化边界,f[0,j] = 0因为没有白鼠了算龙赢,f[i, 0] = 1因为抓一只就是白鼠,公主赢。考虑f[i, j]的转移(每一轮公主和龙轮流拿,可以分成四种情况):
情况一:公主抓到了一只白鼠,公主赢了(龙不用抓了),这种情况发生的概率为:i / (i + j)。
情况二:公主抓到了一只黑鼠,龙抓到了一只白鼠(龙胜利了),这种情况发生的概率为:j / (i + j) * i / (i + j -1)。
情况三:公主抓到了一只黑鼠,龙抓到了一只黑鼠,跑出来了一只白鼠,转移到了f[i - 1, j - 2],这种情况发生的概率:j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2)。
情况四:公主抓到了一只黑鼠,龙抓到了一只黑鼠,跑出来了一只黑鼠,转移到了f[i, j - 3],这种情况发生的概率:j / (i + j) * (j - 1) / (i + j - 1) * (j - 2) / (i + j - 2)。
考虑公主赢的概率,第二种情况不参与计算。并且要保证后两种情况合法,所以还要判断i, j的大小,满足第三种情况至少要有 3 只黑鼠,满足第四种情况要有 1 只白鼠和 2 只黑鼠。
具体的代码实现如下:
#include POJ 3071 Football

先说说这道题的题意:有2n次方个队,已知任意两个队之间每个队获胜的概率,比赛的规则是相邻的两个队伍之间比赛,赢的继续下一轮,输的直接淘汰(相邻的两个队伍是指,1和2,3和4,5和6…如果1和2中假设1赢了,1再跟3和4中的赢家比赛,这样最后赢的那个队一共打了n场比赛。题目的输入是一个2 n的矩阵,第i行第j列的小数表示第i队战胜第j队的概率,所以p[i][j] + p[j][i] == 1。要我们通过概率求得哪一支队伍最终取得冠军的概率最大。
我们用dp[i][j]表示j参加的第i场比赛赢的概率,那么有递推方程dp[i] [j] = dp[i - 1][j] * dp[ i - 1][k] * p[j][k],j能参加的第i场比赛,那么j参加的第i - 1场肯定赢,所以此时有dp[i - 1][j],第i场比赛j的对手是k,k能参加第i场比赛,那么k参加的第i - 1场比赛也肯定赢,所以此时有dp[i - 1][k],因为我们是假设第i场比赛i战胜j,所以有p[j][k]。
这道题的关键是判断第i轮,哪两支队可能进行比赛,因为每场比赛只允许相邻两支上一轮获胜的队伍比赛。这需要用到位运算,我们把1 ~ 2n支队伍的编号变成0 ~ 2n - 1,再把每支队伍的编号看成是二进制(第5支队伍的编号为:101),假设n = 3, 所以第一轮比赛的队伍:000 vs 001,010 vs 011,100 vs 101,110 vs 111。我们发现两两比赛的队伍的编号只有最后一位是不同的;假设第一轮获胜的队伍是第1支(编号为0,二进制:000),第4支(编号为3,二进制:011),第6支(编号为5,101),第7支(编号为6,110),所以此时第二轮比赛:000 vs 011,101 vs 110,这时我们又发现这一轮两两比赛的队伍的编号只要倒数第二位是不同的,以此类推…最终我发现了规律:第i轮比赛能进行比赛的队伍j和k需满足:(((j - 1) >> (i - 1)) ^ 1) == ((k - 1) >> (i - 1)),j - 1和k - 1的含义相当于我们上面第i支队伍的编号为i - 1,当进行到第i轮的时候,我们判断的是编号的倒数第i位(编号右移i - 1,看最后一位(与1异或之后)是否与其他队伍的编号相同),这一系列的操作就是为了判断两支队伍的编号的二进制是不是除了倒数第i位(倒数第i位之后的数不管)之外,前面的都一样,若满足条件,这两支队伍在第i轮就有可能进行比赛。
最后遍历dp[n][i],找到最大的概率,记录并输出dp[n][i]中的i即可。
具体的代码实现如下:
#include CodeForces 768 D - Jon and Orbs
题目大意:有k种物品,每天只能取一种物品,取后放回,有q组询问,每次给出一个数pi,求取物品的期望天数n满足全取完k种物品的概率不小于pi / 2000。
我们用dp[i][j]表示第i天已经出现了j种物品的概率,状态转移方程:dp[i][j] = dp[i - 1][j] * j / k + dp[i - 1][j - 1] * (k - j + 1) / k;所以我们要开始从第一天开始遍历,终止条件是p <= 1000(题目给出了p1的范围),这道题相当于在动态转移的过程中打表了当1 <= p <= 1000时的所有情况。在特定的前i天对已经取得了j(1 ~ k)种物品进行递推求出概率,到最后求出来dp[i][k]之后进行while(p <= 1000 && dp[i][k] * 2000 > p) s[p++] = i; 把符合概率条件的p记录为i。
具体的代码实现如下:
#include POJ2096 Collecting Bugs
看英文看了半天的废话,这道题的大意就是:一个软件有s个子系统,会产生n种bug。某人一天发现一个bug,这个bug属于某种bug分类,也属于某个子系统。每个bug属于某个子系统的概率是1 / s,属于某种bug分类的概率是1 / n。求发现n种bug,且s个子系统都找到bug的期望天数。
这道题就属于期望dp中,终止状态确定时用逆推刷表。我们用dp[i][j]表示以及找到了i中bug分类,这些bug属于j个子系统时,达到目标状态的期望天数。我们这道题的目标是找到n中bug分类,s个子系统的bug。那么就有dp[i][j] = 0,因为此时已经达到了目标状态,不需要更多的天数去发现bug了,达到目标状态的期望天数自然就为0。于是就已目标状态为起点开始递推,答案是dp[i][j]。
dp[i][j]的状态转移情况:
1、dp[i][j],发现一个bug属于已经发现的i种bug分类,j个子系统,这情况发生的概率是:p1 = i / n * j / s
2、dp[i][j + 1],发现一个bug属于已经发现的i种bug分类,但不属于已经发现的j个子系统,这种情况发生的概率是:p2 = i / n * (s - j) / s
3、dp[i + 1][j],发现一个bug不属于已经发现的i中bug分类,属于已经发现的j个子系统,这种情况发生的概率是:p3 = (n - i) / i * j / s
4、dp[i + 1][j + 1],发现的一个bug既不属于已经发现的i个子系统,也不属于已经发现的j个子系统,这种情况发生的概率是:p4 = (n - i) / i * (s - j) / j
因为我们是从终止状态逆推到初始状态的,每一个状态到终止状态期望的天数,都是由它转移到若干状态的概率 与 其对应状态到终止状态期望天数的乘积 相累加得到的(因为是再找一个bug才能转移,所以还要加1),所以我们可以得到状态转移方程:dp[i][j] = p1 * dp[i][j] + p2 * dp[i][j + 1] + p3 * dp[i + 1][j] + p4 * dp[i + 1][j + 1] + 1,把等式两边的dp[i][j]合并可得最终的状态转移方程:dp[i][j] = (dp[i][j + 1] * i * (s - j) + dp[i + 1][j] * (n - i) * j + dp[i + 1][j + 1] * (n - i) * (s - j) + n * s) / (n * s - i * j);
最终得到的dp[0][0]即为发现n种bug,且s个子系统都找到bug的期望天数。
具体的代码实现如下:
#include P1850 [NOIP2016 提高组] 换教室
题目比较长,我先说说大概的意思:牛牛要上n个时间段的课,第i个时间段在ci号教室,可以申请换到di号教室,申请成功的概率为pi,至多可以申请m节课进行交换。第i个时间段的课上完后要走到第i + 1个时间段的教室,给出一张图v个教室e条路,移动会消耗体力,申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小,也就是求出最小的期望路程和。
对于这个无向连通图,先用Floyd求出最短路,为后续状态转移带来便利(我们用f[a][b]表示第a间教室到第b间教室之间的距离)。假设现在在第i - 1个时间段,考虑去第i个时间段上课,如果申请从ci号教室交换到第di号教室上课,则有pi的概率申请成功,1 - pi的概率申请不成功,而且每人只有m个申请的机会(无论申请成功与否,都看作用了申请的机会),求出到第n个时间段走过的最小期望路程和。我们定义dp[i][j][0]表示前i个时间段已经申请了j次,且第i个时间段不申请换教室;dp[i][j][1]表示前i个时间段已经申请了j次,且第i个时间段申请换教室。最终最小的期望路程和就是min{dp[n][j][0], dp[n][j][1]},j的取值范围是0 ~ m。注意初始化边界dp[1][0][0] = dp[1][1][1] = 0。
现在考虑dp[i][j][0/1]的状态转移:
一:dp[i][j][0],第i个时间段不换教室,此时的状态可能是第i - 1个时间段没申请换教室转移来的,也有可能是第i - 1个时间段申请换教室(有pi - 1概率申请成功)转移来的。前者为:dp[i - 1][j][0] + f[c[i - 1]][c[i]],对于后者的情况:如果申请成功,f[d[i - 1]][c[i]] * p[i - 1];如果申请失败,f[c[i - 1]][c[i]] * (1 - p[i - 1]),综合起来,后者为:dp[i - 1][j ][1] + f[d[i - 1]][c[i]] * p[i - 1] + f[c[i - 1]][c[i]] * (1 - p[i - 1])。取前者和后者路程期望的最小值,所以情况一的转移方程:dp[i][j][0] = min(dp[i - 1][j][0] + f[c[i - 1]][c[i]], (dp[i - 1][j][1] + f[d[i - 1]][c[i]] * p[i - 1] + f[c[i - 1]][c[i]] * (1 - p[i - 1])));
二:dp[i][j][1],第i个时间段申请换教室,此时的状态可能是第i - 1个时间段没申请换教室转移来的,也有可能是第i - 1个时间段申请换教室(有pi - 1概率申请成功)转移来的。前者:如果第i个时间段申请成功,f[c[i - 1]][d[i]] * p[i],如果第i个时间段申请不成功,f[c[i - 1][c[i]]] * (1 - p[i]),综合起来,前者:dp[i - 1][j - 1][0] + f[c[i - 1]][d[i]] * p[i] + f[c[i - 1]][c[i]] * (1 - p[i])。后者要分成四种情况(第i - 1和i个时间段都申请换教室了,都有申请成功和失败两种情况),如果都申请成功,f[d[i - 1]][d[i]] * p[i - 1] * p[i];如果都申请失败,f[c[i - 1]][c[i]] * (1 - p[i]) * (1 - p[i - 1]);如果第i - 1个时间段申请成功,第i个时间段申请失败,f[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]);如果第i - 1个时间段申请失败,第i个时间段申请成功,f[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i],综合四种情况起来,后者为:dp[i - 1][j - 1][1] + f[c[i - 1]][c[i]] * (1 - p[i]) * (1 - p[i - 1]) + f[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i] + f[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]) + f[d[i - 1]][d[i]] * p[i - 1] * p[i]。取前者和后者路程期望的最小值,所以情况二的转移方程:dp[i][j][1] = min(dp[i - 1][j - 1][0] + f[c[i - 1]][d[i]] * p[i] + f[c[i - 1]][c[i]] * (1 - p[i]), dp[i - 1][j - 1][1] + f[c[i - 1]][c[i]] * (1 - p[i]) * (1 - p[i - 1]) + f[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i] + f[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]) + f[d[i - 1]][d[i]] * p[i - 1] * p[i]);
最后,取dp[n][j][0/1]的最小值(j的范围:1 ~ m)即为最终的答案。
具体的代码实现如下:
#include HDU3853 LOOPS
这道题的意思是:有一个R * C的迷宫布局,有个人想从起点(1, 1)出发,走到终点(R, C),他要走的话只能向下或者向下走,但每个格子都有让人停留在原地,往右走一个,往下走一格的概率,已知每走一格消耗2点能量,求出最后所需要的能量期望。
输入的时候,首先输入的是R和C,然后依次给出如果经过每个格子的时候,停在原地、向右走、向下走的概率,我们可以用一个三维数组a[i][j][0/1/2]把概率存起来,第三维012分别表示停在原地、向右走、向下走。这道题是期望dp,用逆推的思想求的期望,用dp[i][j]表示当人走到第i行第j列个格子的时候,要到终点(r, c)所需的期望能量,所以dp[r][c] = 0,我们目标是求dp[1][1]。状态转移:dp[i][j] = dp[i][j] * a[i][j][0] +dp[i][j + 1] *a[i][j][1] + dp[i + 1][j] * a[i][j][2] + 2。化简后可得:dp[i][j] = (dp[i][j + 1] * a[i][j][1] + dp[i + 1][j] * a[i][j][2] + 2) / (1 - a[i][j][0]);最后得到的dp[1][1]即为(1, 1)到终点(r, c)的能量期望。
具体的代码实现如下:
#include 总结:
DP求期望的题目在对具体是求一个值或是最优化问题上会对方程得到转移方式有一些影响,但无论是DP求概率还是DP求期望,总是离不开概率知识和列出、化简计算公式的步骤,在写状态转移方程时需要思考的细节也类似。