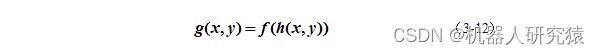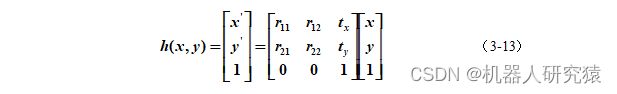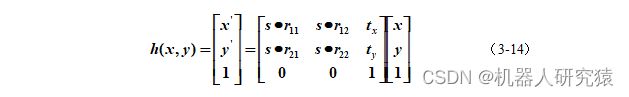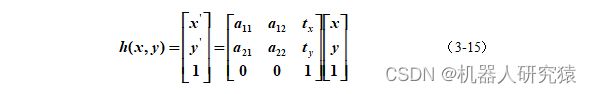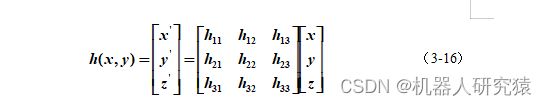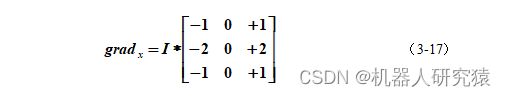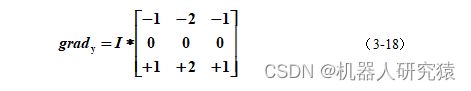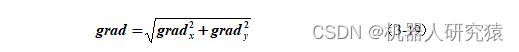一起自学SLAM算法:3.3 图像变换
连载文章,长期更新,欢迎关注:
写在前面
第1章-ROS入门必备知识
第2章-C++编程范式
第3章-OpenCV图像处理
3.1 认识图像数据
3.2 图像滤波
3.3 图像变换
3.4 图像特征点提取
...
更多精彩内容,持续更新中......
大家如有任何技术问题,欢迎加入QQ技术群(117698356),进群一起交流讨论
经过3.2节图像滤波的学习,相信大家对图像处理有了一定的了解。不过,图像滤波只是很初级的处理,其目的是提升图像本身的质量。本节要讲到的图像变换,从改变图像的结构入手,将图像变换成不同的形态。由于篇幅限制,这里重点讲在后续视觉SLAM章节中涉及到的图像变换算法。其他一些常用图像变换算法将略过,比如频谱变换、小波变换、图像金字塔等,感兴趣可以查阅相关资料。
3.3.1 射影变换
这里从基本概念入手,逐步对仿射变换的原理进行解析。首先需要了解的就是重映射(remap),就是把原图中某个位置的像素放到另一个位置,这样原图的所有像素经过重映射操作得到目标图像。原图中的像素与目标图像的像素存在一个对应关系,如式(3-12)所示,其中h(x,y)表示原图像素位置与目标图像像素位置的映射关系,比如图像沿水平方向翻转或沿垂直方向翻转就是最典型的映射。
知道重映射是把原图中某个位置的像素放到另一个位置过程,接下来就可以介绍一些更实用的重映射方法,即欧式变换、相似变换、仿射变换和射影变换。这些变换可以用h(x,y)来表示,欧式变换是最简单的,其实就是对二维图像平面做旋转和平移,如式(3-13)所示。
相似变换,是在欧式变换的基础增加了尺度变换,也就是缩放。很简单,只需要在变换矩阵中加入尺度因子s就行了,如式(3-14)所示。
仿射变换,是在相似变换的基础上,将其中的缩放扩展为更一般性的情况,即非均匀缩放,如式(3-15)所示。这里举个例子来说明非均匀缩放,比如一个长方形经过非均匀缩放可以变成平行四边形。
射影变换,是对仿射变换更一般的推广。其将仿射变换中的变换矩阵的零元素变成了非零元素,这样让射影变换能有非线性的效应出现,如式(3-16)所示。从公式中不难发现,对坐标点引入了z坐标值。其实,射影变换在三维空间中就容易理解了。可以把原图像和目标图像看做三维空间中的两种图像,过某一个公共点进行中心投影,这样就能把原图像中的点投射到目标图像上,这也正是射影变换名字的由来。
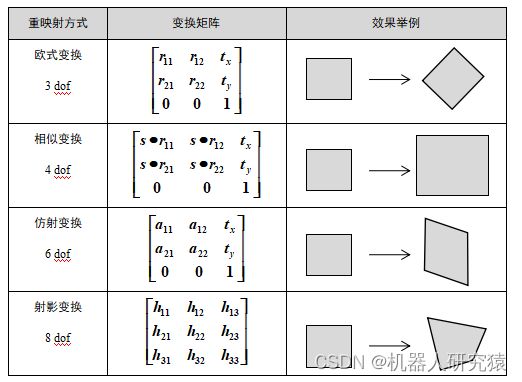
讲到这里,不难发现,射影变换是最一般的形式,也就是说欧式变换、相似变换和仿射变换是射影变换的特例。这里对这几中重映射方式做一个总结,如表3-1所示,图像射影变换及其特例总结。
表3-1 图像射影变换及其特例总结
不难发现,只要会用射影变换对图像进行变换,欧式变换、相似变换和仿射变换这些特例自然也能用射影变换实现。进行射影变换的关键是要知道变换矩阵,通过原图像的4个点与目标图像的4个点,就能求得射影变换矩阵。有了射影变换矩阵,就很容易得到目标图像了。求射影变换矩阵的方法已经被封装到OpenCV的getPerspectiveTransform函数,函数原型如下:
Mat getPerspectiveTransform(const Point2f* src,const Point2f* dst)射影变换被封装到OpenCV的warpPerspective函数,函数原型如下:
void warpPerspective(InputArray src,
OutputArray dst,
InputArray M,
Size dsize,
int flags=INTER_LINEAR,
int borderMode=BORDER_CONSTANT,
const Scalar& borderValue=Scalar())3.3.2 霍夫变换
在很多场合,提取图像中的直线特征非常有用,霍夫变换就是很好的解决办法。在极坐标下,直线用![]() 表示。过固定点
表示。过固定点![]() 有一簇直线,这一簇直线的参数
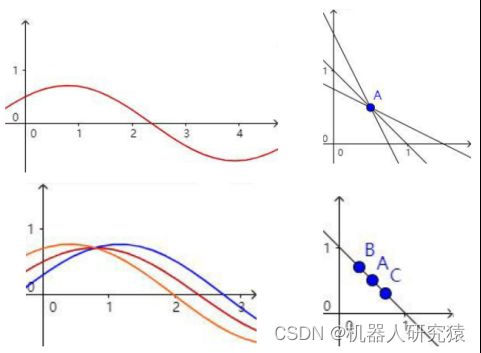
有一簇直线,这一簇直线的参数![]() 可以绘制出一条正弦曲线。同理,过固定点B、C等等都可以得到一簇直线,当直线簇绘出来的正弦曲线相交时,说明A、B、C等这些点过同一条直线,如图3-4所示。霍夫变换就是通过这样的方法,来检测直线的。
可以绘制出一条正弦曲线。同理,过固定点B、C等等都可以得到一簇直线,当直线簇绘出来的正弦曲线相交时,说明A、B、C等这些点过同一条直线,如图3-4所示。霍夫变换就是通过这样的方法,来检测直线的。
图3-4 霍夫变换提取直线原理
在实际的操作中,考虑容错和干扰因素,算法会做一些调整优化。在OpenCV中,标准霍夫变换和多尺度霍夫变换被封装在HoughLines函数中,而累计概率霍夫变换被封装在HoughLinesP函数中。由于累计概率霍夫变换拥有更高的执行效率,所以推荐直接使用累计概率霍夫变换,函数原型如下:
void HoughLinesP(InputArray image,
OutputArray lines,
double rho,
double theta,
int threshold,
double minLineLength=0,
double maxLineGap=0)3.3.4 边缘检测
利用边缘检测,能提取图像中的轮廓,而图像轮廓可以用于分割图像中的物体或者理解图像的意义。常用的两种边缘检测算法是sobel算法和canny算法。
sobel算法是利用微分求导的方式来近似求解图像的梯度。计算也很简单,先分别求解x和y方向的导数,其实就是用x和y方向的卷积核分别对图像I进行卷积操作即可,然后两个方向的导数合成就是该图像点的近似梯度。
1)求x方向导数:
2)求y方向导数:
3)近似梯度:
canny算法为了提高边缘检测的效果,在sobel算法的基础上,做了大量的优化。先用高斯滤波去除图像的噪声;然后用sobel算法求图像的梯度幅值和方向,这里的梯度方向将用于判断像素之间的连接性;接着将候选边缘像素挑选出来,排除非边缘像素;最后使用滞后阈值的方式将最终的边缘像素提取出来,滞后阈值有两个阈值,即高阈值和低阈值,大于高阈值的像素被保留为边缘像素,小于低阈值的像素被排除,而介于两个阈值之间的像素,如果该像素与边缘像素相连接则被保留下来。
sobel算法被封装到OpenCV的Sobel函数,函数原型如下:
void Sobel(InputArray src,
OutputArray dst,
int ddepth,
int dx,
int dy,
int ksize=3,
double scale=1,
double delta=0,
int borderType=BORDER_DEFAULT)canny算法被封装到OpenCV的Canny函数,函数原型如下:
void Canny(InputArray image,
OutputArray edges,
double threshold1,
double threshold2,
int apertureSize=3,
int ksize=3,
bool L2gradient=false)3.3.5 直方图均衡
图像直方图是表示图像中亮点分布的统计图,横坐标是亮度值,纵坐标是每个亮度值对应的像素总数量,如图3-5所示。直方图能反映图像中像素强度的统计信息,是非常重要的统计特征,可以利用这种统计特征判断两幅图的相似性。
图3-5 图像直方图
从图3-5可以看出,图像的像素亮度大都集中在0~150之间,也就是图像整体偏暗。经过直方图均衡后,图像的像素亮度更均匀的分布于0~255区间,图像整体明暗度也更加分明,如图3-6所示。
图3-6 图像直方图均衡
计算直方图的方法被封装在OpenCV的calcHist函数,函数原型如下:
void calcHist(const Mat* images,
int nimages,
const int* channels,
InputArray mask,
OutputArray hist,
int dims,
const int* histSize,
const float** ranges,
bool uniform=true,
bool accumulate=false)图像直方图均衡的方法被封装在OpenCV的equalizeHist函数,函数原型如下:
void equalizeHist(InputArray src,OutputArray dst)参考文献
【1】 张虎,机器人SLAM导航核心技术与实战[M]. 机械工业出版社,2022.