回声消除学习记录

---

一、概述

声学前端算法主要指的是3A算法，即AEC（回声消除），ANS（自适应噪声抑制)和AGC (自动增益控制) 3类算法。其中,回声抵消器是前端声学信号处理的核心,也是各类智能语音终端设备所必需的关键模块。

国内的研究团队的研究重点主要在语音识别和和语义分析的算法研究上,对声学前端信号处理的环节重视程度不够,缺少对声学前端信号处理的理论、技术和方法的系统性研究。

二、基础知识

1.介绍

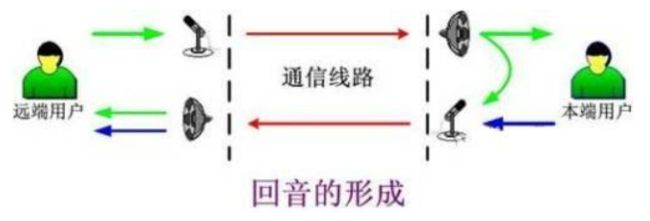
会议双方分处远端和近端，远端说话人的语音传输至近端，经由近端扬声器放出,同近端说话人的语音·一起被近端麦克风拾取，经过传输由远端的扬声器放出。此时远端说话人会同时听到近端说话人的语音和自己语音的回声。

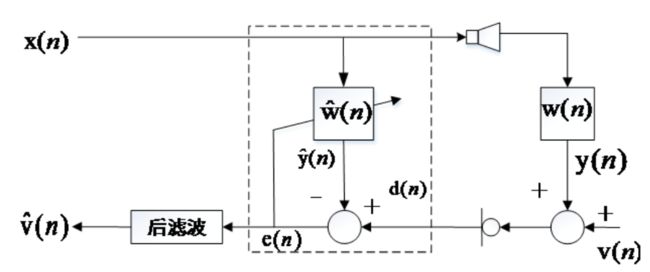
2.经典回声消除算法处理架构

代码如下（示例）：

3.回声评价指标：

1.失调系数：代表回声抵消算法估计出的回声路径接近真实路径的程度

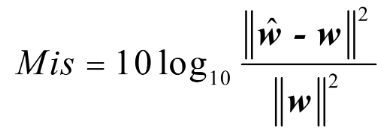
2.回波返回损失:代表回声抵消器以多大的增益从麦克风信号中移除回声

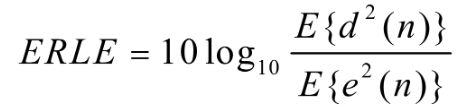
3.计算复杂度

三、回声消除算法

1.LMS算法

LMS算法由美国斯坦福大学的Widrow和Hopf提出，此算法简单实用，是自适应滤波器的标准算法。
$$e(n)=y(n)-\hat{y}(n)=y(n)-{\mathbf{w}}_n^T\mathbf{x}(n)$$
用最陡下降法对滤波器系数${\mathbf{w}}_n$进行如下式的更新:
$${\hat{\mathbf{w}}}_{n+1}={\hat{\mathbf{w}}}_n-\mathbf{g}(n)\mu (n)$$
迭代的梯度向量计算如下:
g ( n ) = ∂ E { ∣ e 2 ( n ) ∣ } ∂ w ^ n ∗ = ∂ E { e ( n ) e ∗ ( n ) } ∂ w ^ n ∗ = − E { e ( n ) x ∗ ( n ) } \boldsymbol{g}(n)=\frac{\partial E\left\{\left|e^2(n)\right|\right\}}{\partial \hat{\boldsymbol{w}}_n^*}=\frac{\partial E\left\{\mathrm{e}(n) e^*(n)\right\}}{\partial \hat{\boldsymbol{w}}_n^*}=-E\left\{e(n) \boldsymbol{x}^*(n)\right\} g(n)=∂w^n∗​∂E{ ​e2(n) ​}​=∂w^n∗​∂E{e(n)e∗(n)}​=−E{e(n)x∗(n)}
故滤波器系数的更新计算如下式所示:
$$\begin{array}{rl}{\hat{\mathbf{w}}}_{n+1}& ={\hat{\mathbf{w}}}_n+\mu (n)E\left\{e(n){\mathbf{x}}^{\ast }(n)\right\}\\ & ={\hat{\mathbf{w}}}_n+\mu (n)e(n)\mathbf{x}(n)\end{array}$$
LMS算法实现结构简单、实用。
有两点明显不足:
1）LMS算法采用瞬时值代替期望值的策略引入了随机波动, 严重影响收玫性能。输入信号过大将引起梯度放大, 输入信号过小又会导致收玫速度降低。
2） 每一个系数的更新, 都需要 $\mathrm{N}$ (滤波器阶数)次乘法, 随着滤波器阶数的增加, 计算复杂 度将显著增加, 这会导致此类系统在长延时回声的环境下, 不能及时消除回声, 使得 系统无法满足实时性的要求。

2.NLMS算法

NLMS算法LMS算法用样本瞬时值来估计,在平均意义上是无偏的,但是会引入随机波动,影响收敛后的性能。针对此不足, NLMS做了相应的改进,修正计算如下：

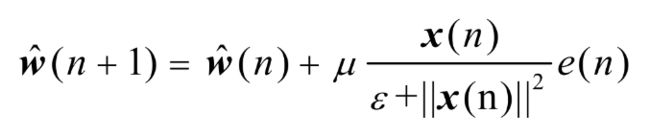
NLMS算法也是逐点更新,计算误差需要N次实数乘法,系数更新要N次实数乘法,计算自适应步长需要N次实数乘法,每次迭代共需3N次乘法,处理一个N点的序列，共需点实数乘法。

3.RLS算法

RLS算法最小二乘(LS)算法旨在使期望信号与模型滤波器输出之差的平方和达到最小。当每次迭代中接收到输入信号的新采样值时,可以采用递归形式求解最小二乘问题,得到递归最小二乘（RLS)算法。对于最小二乘算法,其目标函数是确定性的,并且由下式给出:

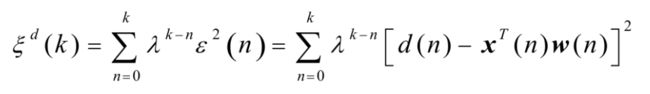
4.FDNLMS算法

FDNLMS算法将参考信号分割成N点的块,滤波器系数每N点更新一次,用N个样点的累加进行更新,这样处理可以有效利用FFT计算,也同NLMS算法具有相同的收敛速度。分块后,第p块的滤波输出值为第p块参考数据与对应滤波器系数的线性卷积(块内保持不变)，计算方法如下：

FDNLMS大大降低NLMS的运算复杂度，但仍有不足：
1)限制硬件的使用: FFT点数需为回声路径尾长的两倍,大多数可用的FFT或DSP芯片都是针对小尺寸FFT设计和优化的,通常小于256点。此时,实现几千个抽头的声学回声消除器是相当低效且昂贵的。
2)影响实时性能:由于FLMS算法实现块处理,如果滤波器长度为1024,则每次处理需等待1024个样本点,在16k采样之下便是64ms的延时。如此长的延迟会严重影响设备的实时性能。
3) FFT的量化误差:随着FFT的尺寸增加,乘法和缩放的数量增加,会导致额外的量化误差，影响计算精度。

5.PBFDAF算法

PBFDAF算法在处理长回声时,为了收集足够的处理数据, BFDAF将带来巨大的处理延迟,不适用于要求实时处理的场合。故在此基础上改进得到分段块频域滤波算法算法基本思想:在频域滤波之前,将自适应滤波器的系数分成相等的长度,补零后变换到频域进行类似于NLMS算法的计算