定位：(plücker coordination)直线的普吕克表示与正交表示，及其相互转换

---

前言

3D空间下的直线可以用普吕克$(\mathbf{n},\mathbf{d})$表示，方便参与几何运算，但其维度为6，在优化中普吕克表达不占优，而正交表示$(\mathbf{U},\mathbf{W})$有4个自由度，主要参与优化运算。本文主要记录以下几点

• 线的普吕克表示
• 与线的正交表示
• 两者之间的关系及相互转换过程

---

一、向量的叉乘与点乘

面的讲解会用到叉乘与点乘，为了避免陌生感，首先来复习一下向量的基本运算：
$$\begin{gathered} \mathbf{a}\cdot \mathbf{b}=\mathbf{b}\cdot \mathbf{a} \\ \mathbf{a}\times \mathbf{b}=-\mathbf{b}\times \mathbf{a} \\ \mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})=(\mathbf{a}\times \mathbf{b})\cdot \mathbf{c} \\ \mathbf{a}\times (\mathbf{b}\times \mathbf{c})=(\mathbf{a}\cdot \mathbf{c})\mathbf{b}-(\mathbf{a}\cdot \mathbf{b})\mathbf{c} \end{gathered}$$

---

二、普吕克坐标系(plücker coordination)

1. 定义

3D空间中刚体有6个自由度，而线有4个自由度，因为线绕自己旋转(roll)，或在线的方向上平移还是同一个直线，因此少了两个自由度。

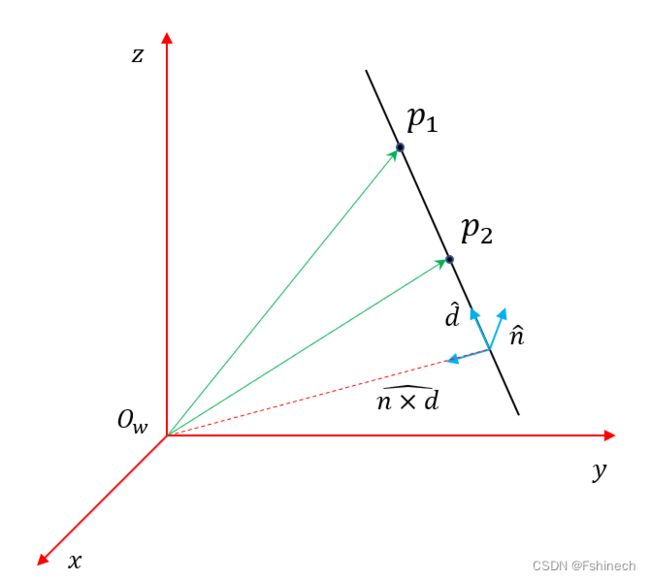
plücker coordination是Julius Plücker在19世纪定义的，也叫Grassmann coordinates。普吕克坐标系定义为$(\mathbf{n},\mathbf{d})$，$\mathbf{n}$为矩向量 (moment vector) 也是法向量，$\mathbf{d}$为线 $\ell$ 的方向向量。具体：已知线上两点 $p_1,p_2$，则线的方向向量 $\mathbf{d}$：
$$\mathbf{d}={\mathbf{p}}_1-{\mathbf{p}}_2\text{\hspace{1em}(1)}$$
法向量 $\mathbf{n}$：
$$\mathbf{n}=\mathbf{p}\times \mathbf{d}\text{\hspace{1em}(2)}$$

其中，$\mathbf{n}$ 垂直于线 $\ell$ 与坐标原点所形成的平面。$\mathbf{p}$ 为线上任一点（可以是$p_1$或$p_2$）在世界坐标的向量表示。点$p$可以任意选取的原因在于，线上任一点 $p^{\prime }$ 满足 ${\mathbf{p}}^{\prime }-\mathbf{p}=\lambda \mathbf{d}$：
$$\begin{array}{rl}{\mathbf{p}}^{\prime }\times \mathbf{d}& =(\mathbf{p}+({\mathbf{p}}^{\prime }-\mathbf{p}))\times \mathbf{d}\\ & =\mathbf{p}\times \mathbf{d}+({\mathbf{p}}^{\prime }-\mathbf{p})\times \mathbf{d}\\ & =\mathbf{n}+\lambda \mathbf{d}\times \mathbf{d}\\ & =\mathbf{n}\end{array}\text{\hspace{1em}(3)}$$

2. 性质

2.1. 一点 $p$ 在线 $\ell$ 上的充分必要条件：$\mathbf{q}\times \mathbf{d}=\mathbf{n}$。
2.2. 坐标原点到 $\ell$ 的距离为$\frac{||\mathbf{n}||}{||\mathbf{d}||}$。
2.3. 线$(\mathbf{n},\mathbf{d})$与线$(\alpha \mathbf{n},\alpha \mathbf{d}),\alpha \ne 0$ 表示的是同一直线。
2.4. 线 $\ell$ 与过原点的垂线的交点（垂足）记为$p_{\perp }$，则：

$$\begin{array}{rl}{\mathbf{p}}_{\perp }& =\mathbf{p}-(\mathbf{d}\cdot \mathbf{p})\mathbf{d}\\ & =(\mathbf{d}\cdot \mathbf{d})\mathbf{p}-(\mathbf{d}\cdot \mathbf{p})\mathbf{d}\\ & =\mathbf{d}\times (\mathbf{p}\times \mathbf{d})\\ & =\frac{\mathbf{d}}{||\mathbf{d}||}\times (\mathbf{p}\times \frac{\mathbf{d}}{||\mathbf{d}||})\\ & =\frac{\mathbf{d}}{||\mathbf{d}||}\times \frac{\mathbf{n}}{||\mathbf{d}||}\\ & =\frac{\mathbf{d}\times \mathbf{n}}{||\mathbf{d}|{|}^2}\end{array}\text{\hspace{1em}(4)}$$

2.5. $\mathbf{n}=0$时，直线 $\ell$ 经过坐标原点。 那么，经过坐标原点的线的普吕克表示为$(0,\_)$。
2.6. 平面 $\Pi$ 经过坐标原点，那么位于面 $\Pi$ 上的所有无穷远处的直线的具有相同的普吕克表示为 $(\mathbf{n},0)$, $\mathbf{n}$ 为面 $\Pi$ 的法线。
2.7. 直线 $\ell$ 关于空间任一点 $q$ 的矩向量（moment vector）为${\mathbf{n}}_q$，$q$ 在$\ell$ 上的投影为$q_{\perp }$，则：
$$\begin{array}{rl}{\mathbf{n}}_q& =(\mathbf{p}-\mathbf{q})\times \mathbf{d}\\ & =\mathbf{p}\times \mathbf{d}-\mathbf{q}\times \mathbf{d}\\ & =\mathbf{n}-\mathbf{q}\times \mathbf{d}\end{array}\text{\hspace{1em}(5)}$$
又，
$$\begin{array}{rl}\mathbf{d}\times {\mathbf{n}}_q& =\mathbf{d}\times ({\mathbf{q}}_{\perp }-\mathbf{q})\times \mathbf{d}\\ & =(\mathbf{d}\cdot \mathbf{d})({\mathbf{q}}_{\perp }-\mathbf{q})-(\mathbf{d}\cdot ({\mathbf{q}}_{\perp }-\mathbf{q}))\mathbf{d}\\ & ={\mathbf{q}}_{\perp }-\mathbf{q}\end{array}\text{\hspace{1em}(6)}$$
因此，
$${\mathbf{q}}_{\perp }=\mathbf{q}+\mathbf{d}\times {\mathbf{n}}_q\text{\hspace{1em}(7)}$$
直线的普吕克表示适合几何运算，但不适合优化，而直线的正交表示可以应用到优化过程。

3. 世界坐标系下线的普吕克坐标转换到相机坐标系

已知世界坐标系到相机坐标系的变换矩阵${\mathbf{T}}_w^c=\left[\begin{array}{cc}{\mathbf{R}}_w^c& {\mathbf{t}}_w^c\\ 0& 1\end{array}\right]$，世界坐标系下的直线普吕克表示${\mathcal{L}}_w$，则相机坐标系下的普吕克表示${\mathcal{L}}_c$可通过式 $(8)$ 得到：
$${\mathcal{L}}_c=\left[\begin{array}{c}{\mathbf{n}}_c\\ {\mathbf{d}}_c\end{array}\right]={\mathcal{T}}_w^c{\mathcal{L}}_w=\left[\begin{array}{cc}{\mathbf{R}}_w^c& {\left[{\mathbf{t}}_w^c\right]}_{\times }{\mathbf{R}}_w^c\\ 0& {\mathbf{R}}_w^c\end{array}\right]{\mathcal{L}}_w\text{\hspace{1em}(8)}$$
其中，$[{\mathbf{t}}_w^c{]}_{\times }$ 为平移向量 ${\mathbf{t}}_w^c$ 的反对称矩阵(Skew-symmetric matrix)，${\mathcal{T}}_w^c$ 为直线的普吕克坐标从世界坐标系到相机坐标系的变换矩阵。同理，将直线从相机坐标系转换到世界坐标系的变换矩阵${\mathcal{T}}_c^w$，如式(9)所示：
$${\mathcal{T}}_c^w={{\mathcal{T}}_w^c}^T=\left[\begin{array}{cc}{{\mathbf{R}}_w^c}^T& -{\left[{{\mathbf{R}}_w^c}^T{\mathbf{t}}_w^c\right]}_{\times }{{\mathbf{R}}_w^c}^T\\ 0& {{\mathbf{R}}_w^c}^T\end{array}\right]\text{\hspace{1em}(9)}$$

三、线的正交表示

正交表示只需要4个变量$(\mathbf{\theta },\varphi )\in {\mathbb{R}}^3\times {\mathbb{R}}^1$，对应两个正交矩阵$(\mathbf{U},\mathbf{W})\in SO(3)\times SO(2)$，比较适合在优化过程中对线的表示。

1. 普吕克表示转换到正交表示

正交表示和普吕克表示可以相互转换，在SLAM中可灵活应用。正交表示可以通过对普吕克坐标进行QR分解得到，但实际应用中很容易构造如下所示的矩阵：
$$\begin{array}{rl}\left[\mathbf{n}\mathbf{d}\right]& =\left[\begin{array}{ccc}\frac{\mathbf{n}}{||\mathbf{n}||}& \frac{\mathbf{d}}{||\mathbf{d}||}& \frac{\mathbf{n}\times \mathbf{d}}{||\mathbf{n}\times \mathbf{d}||}\end{array}\right]\left[\begin{array}{cc}||\mathbf{n}||& 0\\ 0& ||\mathbf{d}||\\ 0& 0\end{array}\right]\\ & =\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]\left[\begin{array}{cc}||\mathbf{n}||& 0\\ 0& ||\mathbf{d}||\\ 0& 0\end{array}\right]\end{array}\text{\hspace{1em}(10)}$$

因此，很容易得到一个表示旋转的正交矩阵，也就是旋转矩阵 $\mathbf{U}$：
$$\begin{array}{rl}\mathbf{U}& =\mathbf{R}(\mathbf{\theta })={\mathbf{R}}_x({\theta }_1){\mathbf{R}}_y({\theta }_2){\mathbf{R}}_z({\theta }_3)\\ & =\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{\mathbf{n}}{||\mathbf{d}||}& \frac{\mathbf{d}}{||\mathbf{d}||}& \frac{\mathbf{n}\times \mathbf{d}}{||\mathbf{n}\times \mathbf{d}||}\end{array}\right]\end{array}\text{\hspace{1em}(11)}$$

其中，$\mathbf{\theta }$ 为依次绕 $x-y-z$ 轴的旋转角，显然，$\mathbf{R}(\mathbf{\theta })$ 就是绕 $x-y-z$ 旋转后的旋转矩阵。
矩阵$\left[\begin{array}{cc}||\mathbf{n}||& 0\\ 0& ||\mathbf{d}||\\ 0& 0\end{array}\right]$只有一个自由度，将其归一化后可用一个$SO(2)$更新，用三角函数表示为：
$$\begin{array}{rl}\mathbf{W}& =\left[\begin{array}{cc}\cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \end{array}\right]\\ & =\left[\begin{array}{cc}{w}_1& -w_2\\ w_2& w_1\end{array}\right]\\ & =\frac{1}{\sqrt{||\mathbf{n}|{|}^2+||\mathbf{d}|{|}^2}}\left[\begin{array}{cc}||\mathbf{n}||& -||\mathbf{d}||\\ ||\mathbf{d}||& ||\mathbf{n}||\end{array}\right]\end{array}\text{\hspace{1em}(12)}$$

从式 (12) 可以看出 $\mathbf{W}$ 包含了距离信息。故正交表示$(\mathbf{U},\mathbf{W})$包含3自由度的旋转和1自由度的距离。

2. 正交表示转换到普吕克表示

已知线d正交表示$(\mathbf{U},\mathbf{W})$，或$(\mathbf{\theta },\varphi )$，很容易求得普吕克表示：
$$\left[\mathbf{n}\mathbf{d}\right]=\left[w_1{\mathbf{u}}_1^T{w}_2{\mathbf{u}}_2^T\right]\text{\hspace{1em}(13)}$$

其中，$w_1=\cos \varphi ,w_2=\sin \varphi$。

---

总结

本文主要记录了线的普吕克表示和正交表示，以及两者相互转化公式，有不对之处欢迎指正，谢谢！

参考文献

Jia, Yan-Bin. “Plücker Coordinates for Lines in the Space.” (2020).
He, Yijia et al. “PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features.” Sensors (Basel, Switzerland) 18 (2018)