【CV】图像恢复（去噪，去模糊，超分）模型 DPDNN 论文笔记

论文名称：Denoising Prior Driven Deep Neural Network for Image Restoration
论文下载：https://arxiv.org/abs/1801.06756
论文年份：TPAMI 2019
论文被引：9（2022/04/17）
论文代码：
TF：https://github.com/WeishengDong/DPDNN
Torch：https://github.com/WeishengDong/DPDNN_PyTorch

硕士论文：link

图像恢复相关的PPT：https://www.robots.ox.ac.uk/~az/lectures/ia/lect3.pdf

Abstract

Deep neural networks (DNNs) have shown very promising results for various image restoration (IR) tasks. However, the design of network architectures remains a major challenging for achieving further improvements. While most existing DNN-based methods solve the IR problems by directly mapping low quality images to desirable high-quality images, the observation models characterizing the image degradation processes have been largely ignored. In this paper, we first propose a denoising-based IR algorithm, whose iterative steps can be computed efficiently. Then, the iterative process is unfolded into a deep neural network, which is composed of multiple denoisers modules interleaved with back-projection (BP) modules that ensure the observation consistencies. A convolutional neural network (CNN) based denoiser that can exploit the multiscale redundancies of natural images is proposed. As such, the proposed network not only exploits the powerful denoising ability of DNNs, but also leverages the prior of the observation model. Through end-to-end training, both the denoisers and the BP modules can be jointly optimized. Experimental results on several IR tasks, e.g., image denoisig, super-resolution and deblurring show that the proposed method can lead to very competitive and often state-of-the-art results on several IR tasks, including image denoising, deblurring and super-resolution.

深度神经网络 (DNN) 已在各种 图像恢复 (image restoration, IR) 任务中显示出非常有希望的结果。然而，网络架构的设计仍然是实现进一步改进的主要挑战。虽然大多数现有的基于 DNN 的方法通过将低质量图像直接映射到所需的高质量图像来解决 IR 问题，但 表征图像退化过程 (image degradation processes) 的观察模型 在很大程度上被忽略了。在本文中，我们首先提出了一种 基于去噪的 IR 算法，该算法的迭代步骤可以有效地计算。然后，将迭代过程展开为一个深度神经网络，该网络由多个降噪模块和反投影 (back-projection, BP) 模块交织而成，以确保观测一致性。提出了一种基于卷积神经网络 (CNN) 的 去噪 (denoising) 方法，可以利用自然图像的多尺度冗余。因此，所提出的网络不仅利用了 DNN 强大的去噪能力，而且 利用了观察模型的先验。通过端到端的训练，降噪器和BP模块都可以联合优化。在图像去噪、超分辨率和去模糊等几个 IR 任务上的实验结果表明，所提出的方法可以产生了非常有竞争力且通常是最先进的结果。

I. INTRODUCTION

【图像恢复定义】：旨在从低质量观察中重建高质量图像。

【应用场景】：低级图像处理、医学成像、遥感、监控等。

【数学表示】：IR 问题可以表示为 y = Ax + n，其中 y 和 x 分别表示退化图像和原始图像，A表示与成像/退化系统相关的退化矩阵，n表示加性噪声。请注意，对于 A 的不同设置，可以表达不同的 IR 问题。

• 当 A 是恒等映射矩阵（identical matrix）时，IR 问题是 **去噪（denoising）**问题。

• 当 A 是模糊矩阵/算子（blurring matrix/operator）时，IR 问题是 去模糊（denoising） 问题。

• 当 A 是子采样矩阵/算子（subsampling matrix/operator）时，IR 问题是 **超分辨率（super-resolution）**问题。

  本质上，从 y 恢复 x 是一个具有挑战性的 不适定逆问题（ill-posed inverse problem）。在过去的几十年里，IR问题得到了广泛的研究。然而，它们仍然是一个活跃的研究领域。

【图像恢复分类】

• 基于模型的方法：

  • 通过解决优化问题来解决这个问题，优化问题通常是从贝叶斯的角度构建的。在贝叶斯设置中，通过最大化后验 P(x|y) 来获得解决方案，可以用公式表示为：
    

  • 其中 logP(y|x) 和 logP(x) 分别表示数据似然性和先验项。对于加性高斯噪声，P(y|x) 对应于 l2-范数数据保真度项，而先验项 P(x) 表征了概率设置中x的先验知识。形式上，公式(1)可以改写为：

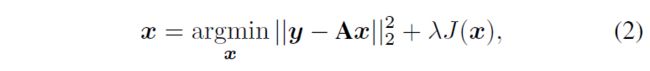
  • 其中 J(x) 表示与先验项 P(x) 相关联的正则化器。然后，理想的解决方案是最小化 l2-范数数据保真项和由参数 λ 加权的正则化项。显然，正则化项在寻找高质量解决方案中起着至关重要的作用。

  • 正则化器	文献	优缺点
    总变差 (total variation，TV) 正则化器	[42]	TV 正则化器擅长表征分段常数信号，但无法对更复杂的图像边缘和纹理进行建模。
    具有现成（off-the-shelf）变换或学习字典的稀疏基正则化器	[3]、[14]、[20]、[ 39]、[60]	基于稀疏性的技术更有效地表示具有来自现成变换矩阵（例如，DCT 和小波）或学习字典的一些元素结构（称为原子）的局部图像结构。
    非局部自相似性（nonlocal self-similarity，NLSS）启发的正则化器	[6]、[10]、[19]
    将 NLSS 与稀疏表示和低秩近似相结合的非局部正则化技术	[10]、[15]、[16]、[19]
    基于去噪的 IR 方法	[5]、[8]、[45]、[51]、[54]

  • 在这些方法中，原始优化问题被解耦为两个独立的子问题——一个用于处理数据保真项，另一个用于正则化项，从而产生更简单的优化问题。具体来说，与正则化相关的子问题是一个纯去噪问题，因此也可以采用其他更复杂的不能表示为正则化项的去噪方法，例如 BM3D [10]、NCSR [19] 和 GMM [66] 方法。

• 基于学习的方法

  • 基于学习的 IR 方法 学习映射函数以从观察到的图像中推断丢失的高频细节或所需的高质量图像。

  • 算法	原理	优缺点
    基于学习的图像超分辨率方法 [12]、[13]、[21]、[27]、[52]、[24]、[49]、[53]、[63]、 [65]	学习从低分辨率（LR）补丁到高分辨率（HR）补丁的映射函数
    DCNN 模型：SRCNN [ 12]、FSRCNN [13]、VDSR [27] 和 EDSR [34] 用于图像超分辨率
    DCNN 模型：TNRD [9]、DnCNN [63] 和 MemNet [50] 用于图像去噪	DCNN 用于学习从退化图像到原始图像的映射函数。	DCNN 方法在适应不同的图像恢复任务方面缺乏灵活性，因为尚未明确利用数据似然项。
    结合基于优化的方法和 DCNN 降噪器的混合 IR 方法	在 [41]、[64] 中，一组 DCNN 模型针对图像去噪任务进行了预训练，并集成到基于优化的 IR 框架中，用于不同的 IR 任务。	解决了上述问题。
    基于自动编码器的 IR 方法 [2]	去噪自动编码器被预训练为自然图像先验，并提出了基于预训练自动编码器的正则化器。然后通过梯度下降迭代地解决由此产生的优化问题。	尽管方法 [2]、[64] 很有效，但它们必须迭代地解决优化问题，因此它们的计算复杂度很高。此外，[2]、[64] 中采用的 CNN 和自动编码器模型是预训练的，不能与其他算法参数联合优化。

【本文提出的方法】

在本文中，我们提出了一种去噪先验驱动的（denoising prior driven）深度网络，以利用基于优化和判别学习的 IR 方法。首先，我们提出了一种基于去噪的 IR 方法，其迭代过程可以有效地进行。然后，我们将迭代过程展开为前馈神经网络，其各层模拟（mimic）所提出的基于去噪的 IR 算法的流程。此外，提出了一种可以利用多尺度冗余的（multi-scale redundancies）有效 DCNN 降噪器并将其插入深度网络。通过端到端的训练，DCNN 去噪器和其他网络参数都可以联合优化。实验结果表明，所提出的方法可以在包括图像去噪、去模糊和超分辨率在内的几个 IR 任务上实现非常有竞争力且通常是最先进的结果。

II. RELATED WORK

简要回顾了与所提出的方法相关的 IR 方法，即基于去噪的 IR 方法和基于判别学习的 IR 方法。

A. Denoising-based IR methods

基于去噪的 IR 方法 [54] 不是使用明确表达的正则化器，而是通过解耦（decoupling）等式的优化问题，允许使用更复杂的图像先验。方程 (2) 分成两个子问题，一个用于数据似然项，另一个用于前项。通过引入辅助变量 v，方程 (2) 可以改写为：

在[8]、[54]中，利用ADMM技术将上述等约束优化问题转化为两个子问题

其中 u 表示增广拉格朗日乘数，更新为 $u^{(t+1)}=u^{(t)}+\rho (x^{(t+1)}-v^{(t+1)})$。 x-子问题是一个简单的二次优化，它有闭式解：

中间重建的图像 $x^{(t+1)}$ 取决于观测模型和 v 的固定估计值。v 子问题也称为 J(v) 的邻近算子，在点 $x^{(t+1)}+u^{(t)}$，其解可以通过去噪算法获得。通过交替更新 x 和 v 直到收敛，解决方程 (2) 的原始优化问题。该框架的优势在于，其他无法在 J(x) 中明确表示的最先进的去噪算法也可用于更新 v，从而获得更好的 IR 性能。

• 例如，众所周知的 BM3D [10]、高斯混合模型 [66]、NCSR [19] 已被用于各种 IR 应用 [5]、[51]、[54]。在 [64] 中，最先进的 CNN 降噪器也被插入作为一般 IR 的图像先验。由于出色的去噪能力，已经获得了针对不同 IR 任务的最先进的 IR 结果。
• 与 [2] 类似，自动编码器降噪器被插入到等式 (2) 的目标函数中。然而，与上面描述的变量分裂方法不同，[2]的目标函数是通过梯度下降来最小化的。
• 尽管基于去噪的 IR 方法在利用现有技术的图像方面非常灵活和有效，但它们需要大量迭代才能收敛，并且无法联合优化整个组件。

B. Deep network based IR methods

【DCNN 的应用场景】：

• 图像分类 [26]、[30]、目标检测 [37]、[44]、语义分割 [38] 等
• 低级图像处理任务 [ 9]、[12]、[27]、[63]
• 与耦合稀疏编码 [60] 类似，DCNN 被提出来学习从 LR 补丁空间到 HR 补丁空间的非线性映射 [12]。
• 在 [63] 中，提出了带有残差学习的 DCNN 用于图像恢复。

---

【图像恢复领域不同的DCNN】：

• 为了提高 SR 性能，已经开发了非常深的 CNN，并取得了最先进的 SR 结果 [27]。
• 为了减轻训练非常深的网络的难度，已经提出了深度递归残差学习来训练非常深的网络用于图像 SR [49]。
• 通过将深度超分辨率架构视为单状态循环神经网络 (RNN)，在 [24] 中提出了一种用于 SR 的双状态 RNN，以联合利用低分辨率和高分辨率信号。
• 为了重用前几层的特征图，还为图像 SR [53] 开发了密集连接网络。
• 与现有的恒等映射快捷连接不同，[65] 中还提出了具有可学习参数的自适应快捷连接用于图像恢复任务。
• 除了常用的均方损失之外，还提出了一种基于生成对抗网络 (GAN) 的使用感知损失函数的 SR 模型，用于逼真的超分辨率自然图像 [31]。
• 为了利用深度 CNN 中的长期依赖关系，在 [50] 中，已经开发了包含内存块的非常深的持久内存网络，从而为典型的图像恢复任务带来了实质性的改进。
• 对于非盲图像去模糊，已经开发了多人感知器网络 [7] 来去除去卷积伪影。在[58]中，建议使用 DCNN 进行非盲图像去模糊（non-blind image deblurring）。

尽管已经获得了出色的 IR 性能，但这些 DCNN 方法通常将 IR 问题视为去噪问题，即去除最初恢复图像的噪声或伪影（artifacts），而忽略观察模型。

---

【尝试利用领域知识和 IR 观察模型】

• 在 [56] 中，基于学习的迭代收缩/阈值算法 (LISTA) [23]，Wang 等人开发了一个深度网络，其层对应于基于稀疏编码的图像 SR 的步骤。
• 在[9]中，经典的迭代非线性反应扩散方法也被实现为深度网络，其参数是联合训练的。
• 受基于 ADMM 的稀疏编码算法启发的 DNN 也被开发用于基于压缩感知的 MRI 重建 [61]。
• 在 [57] 中，用于解决“0 范数稀疏恢复问题”的截断迭代硬阈值算法被实现为 DNN。与原始迭代算法相比，这些基于模型的 DNN 在效率和有效性方面都显示出显着的改进。然而，传统的基于稀疏编码的方法的严格实现导致卷积滤波器的接收域有限，因此不能有效地利用特征图的空间相关性，导致 IR 性能受限。
• 在 [28] 中，在替代最小化框架下提出了基于 DCNN 的学习正则化器，在几个 IR 任务中显示出非常有希望的结果。
• 然而，在所提出的框架中也有一些手工制作的组件，例如用于提取梯度特征的梯度算子和用于从正则化梯度重建图像的预条件共轭梯度 (PCG) 方法。代替在梯度域中学习正则化器，像素域中基于 DCNN 的图像去噪器也被学习为用于图像恢复的凸能量最小化算法的正则化的近端算子 [41]、[64]。

---

III. PROPOSED DENOISING-BASED IMAGE RESTORATION ALGORITHM

在本节中，我们开发了一种有效的迭代算法来解决基于去噪的 IR 方法，下一节将在此基础上提出前馈 DNN。考虑方程 (3) 的基于去噪的 IR 问题，我们采用半二次分裂方法（the half-quadratic splitting），通过这种方法可以将等约束的优化问题转化为无约束的优化问题，如

x-子问题是一个二次优化问题（quadratic optimization），可以用封闭形式求解，如 $x^{(t+1)}=W^{-1}b$，其中 W 是与退化矩阵 A 相关的矩阵。通常，W 很大，所以不可能计算出它的逆矩阵。相反，迭代经典共轭梯度 (CG) 算法可用于计算 $x^{(t+1)}$，这需要多次迭代来计算 $x^{(t+1)}$。在本文中，我们建议使用单步梯度下降来计算 $x^{(t+1)}$，而不是求解 x 子问题的精确解，如

我们不需要精确地解决 x 子问题。更新 $x^{(t+1)}$ 一次足以使 $x^{(t)}$ 收敛到局部最优解。 v-子问题是在点 $x^{(t+1)}$ 计算的 J(v) 的邻近算子，其解可以通过降噪器获得，即 $v(t+1)=f(x^{(t+1)})$, 其中 $f(\cdot )$ 表示降噪器。可以使用各种去噪算法，包括那些不能由带有 J(x) 的 MAP 估计器明确表达的算法。受 DCNN 用于图像去噪的成功启发，本文选择了基于 DCNN 的去噪器来利用大型训练数据集。然而，与现有的 IR 的 DCNN 模型不同，我们考虑可以利用自然图像的多尺度冗余的网络，这将在下一节中描述。总之，用于解决基于去噪的 IR 问题的建议迭代算法总结在算法 1 中，我们将 $x^{(0)}$ 初始化为 $x^{(0)}=A^{T}y$。**

• 对于图像去噪，$x^{(0)}=y$。
• 对于图像SR，$x^{(0)}=A^{T}y=H^T{D}^{T}y$，这可以通过首先用零插值对 $y$ 进行上采样，然后用转置模糊矩阵 $H^T$ 对上采样的图像进行滤波来获得。对于具有双三次 (bicubic) 下采样的图像SR，$x^{(0)}=A^{T}y$ 被实现为具有双三次插值器的图像上采样。
• 对于图像去模糊，$x^{(0)}=A^{T}y=H^{T}y$，这可以实现为 $y$ 与 $H^T$ 的转置卷积。

我们现在讨论算法1的收敛特性。



在第二部分中，如果流形 (mainfold) 是非空的，则 J(x) 是适当的；如果流形的上图是闭的，则 J(x) 是下半连续的。这些条件很容易检查，并且经常得到满足，尽管并不总是如此。也就是说，为了使 ξ 强凸，流形需要是一阶光滑有界的，或者具有全局有界曲率 (globally bound curvatures)。

在 [4] 中已经表明，如果 ξ 具有 Kurdyka-Łojasiewicz (KL) 属性，则子序列收敛可以升级为全序列收敛，这已成为最近收敛分析的标准论点。如[59]所示，满足KL性质的函数包括但不限于实解析函数、半代数函数和局部强凸函数。因此，$(x^{(t)},v^{(t)})$ 收敛到一个固定点。静止点 $(x^{\ast },v^{\ast })$ 可能是鞍点而不是局部极小值。然而，众所周知，假设初始解是随机选择的，一阶方法几乎总是避免鞍点 [32]。因此，收敛到鞍点是极不可能的。

在 [1] 中已经表明，降噪器自动编码器可以被视为噪声输入 y 到无噪声图像流形的近似正交投影。因此，如上述第 2 部分所示，基于上述分析，具有由 DCNN 去噪器定义的映射函数 f(·) 的算法 1 收敛到局部最小化器。

IV. DENOISING PRIOR DRIVEN DEEP NEURAL NETWORK

一般来说，算法 1 需要多次迭代才能收敛，而且计算量很大。而且，参数和降噪器不能以端到端的训练方式联合优化。为了解决这些问题，我们建议将算法 1 展开为图 1 (a) 所示架构的深度网络。网络准确地执行算法 1 的 T 次迭代。输入的退化图像 $y\in R^{n_y}$ 首先经过一个由退化矩阵 $A\in {\mathbb{R}}^{n_y\times m_x}$ 参数化的线性层，用于初始估计 $x^{(0)}$。然后将 $x^{(0)}$ 输入去噪模块和由矩阵 $\overline{A}\in {\mathbb{R}}^{m_x\times m_x}$ 参数化的线性层。由 ${\delta }_{1,1}$ 加权的去噪信号 $v^{(1)}$ 经由快捷连接之后，与由 ${\delta }_{1,2}$ 加权的线性层 ${\overline{A}}^{T}y$ 和 $\overline{A}$ 相加，得到更新后的 $x^{(1)}$。去噪模块的结构如图1(b) 所示。这样的过程重复T次。在我们的实现中，T = 6。与使用固定权重不同，T 个循环阶段中涉及的所有权重 ${\delta }_{1,1}{\delta }_{t,2},t=1,2,\cdot \cdot \cdot ,T$ 可以通过端到端训练有区别地学习。由于使用的是包含大量参数的基于 DCNN 的去噪模块，因此强制所有去噪模块共享相同的参数以避免过拟合。

线性层 A^T 和 ¯A 对于典型的退化矩阵 A 也是可训练的。对于图像去噪，A = A^T = I，并且 ¯A 也简化为加权单位矩阵 ¯A = λI，其中 λ = 1 - δ (1 + η)。对于图像去模糊，层 A^T 可以简单地用卷积层来实现。层¯A = aI - δA^TA 也可以通过卷积运算有效计算。权重 a 和过滤器对应于 A^T 并且 A 也可以有区别地学习。对于图像超分辨率，考虑了两种类型的退化算子：高斯下采样和双三次下采样。对于高斯下采样，A = DH，其中 H 和 D 分别表示高斯模糊矩阵和下采样矩阵。在这种情况下，层 $A^T=H^T{D}^T$ 对应于首先通过零填充对输入 LR 图像进行上采样，然后将上采样图像与滤波器进行卷积。层¯A 也可以通过卷积、下采样和上采样操作来有效计算。这些操作中涉及的所有卷积滤波器都可以有区别地学习。对于双三次下采样，我们简单地使用具有缩放因子 s 和 1/s (s = 2, 3, 4) 的双三次插值函数来分别实现矩阵向量乘法 A^Ty 和 Ax。

A. The DCNN denoiser

受语义分割 [38] 和对象分割 [43] 的最新进展的启发，去噪网络的架构如图 1(b) 所示。请注意，其他更强大的去噪网络也可以用于所提出的 IR 框架中。与 U-net [46] 和 sharpMask net [43] 类似，去噪网络包含两个部分：特征提取和图像重建部分。在特征提取部分，有一系列卷积层，然后是下采样层，以降低特征图的空间分辨率。下采样层有助于增加神经元的感受野。卷积层被分组为 L 个特征编码块（在我们的实现中 L = 6），如图 1（b）中的灰色箭头所示。如图 1© 所示，每个特征编码块包含四个具有 ReLU 非线性的卷积层和 3×3 内核，每个卷积层生成 64 通道特征图。前四个编码块之后是下采样层，以降低特征图的空间分辨率，比例因子为 0.5。在下采样层中，特征图沿两个轴按比例因子 2 进行子采样。

图像重建部分还包含一系列卷积层，它们被分组为四个特征解码块（如图 1(b) 中的绿色箭头所示），然后是上采样层以提高特征图的空间分辨率。由于最终提取的特征图丢失了大量空间信息，直接从提取的特征中重建图像无法恢复精细的图像细节。为了补偿丢失的空间信息，将编码阶段生成的相同空间分辨率的特征图与解码阶段生成的上采样特征图融合，以获得新的上采样特征图。如图 1© 所示，每个解码块由五个卷积层组成。第一层使用 1 × 1 内核和 ReLU 函数将特征图的数量从 128 个减少到 64 个。以下四层生成具有 ReLU 非线性的 3 × 3 内核的 64 通道特征图。最后一层生成的特征图然后通过反卷积层以缩放因子 2 进行上采样。然后将上采样的特征图与来自编码部分的相同空间分辨率的特征图融合。具体来说，融合是通过连接特征图来进行的。输出图像是使用大小为 3×3 的滤波器从 64 通道特征图重建的。我们没有直接重建原始图像，而是强制去噪网络预测残差，这已被证明更鲁棒 [63] 。为此，添加了从输入到重建图像的跳过连接。

B. Overall network training

请注意，DCNN 降噪器不必经过预训练。相反，图 1(a) 所示的整个深度网络是通过端到端训练来训练的。为了减少参数数量从而避免过拟合，我们强制每个 DCNN 降噪器共享相同的参数。采用基于均方误差（MSE）的损失函数来训练所提出的深度网络，可以表示为

其中 yi 和 xi 分别表示第 i 对退化和原始图像块，F(yi; Θ) 表示具有参数集 Θ 的网络重建的图像块。也可以使用其他基于感知的损失函数来训练网络，这可能会导致更好的视觉质量。我们将此作为未来的工作。 ADAM 优化器 [29] 用于训练网络，设置 β1 = 0.9，β2 = 0.999 和 $ϵ$ = 10−8。卷积核由 [25] 中开发的 Xavier 初始化器初始化。与退化矩阵 A 相关的线性层由退化模型 A 初始化。其他参数，即 δ 和 η 分别根据经验初始化为 0.1 和 0.9。建议的网络以 16 的 minibatch 大小进行训练。学习率 $ϵ$ 初始化为 0.0005，每 43000 次小批量更新减半。提出的网络在 Tensorflow 框架下实现，并使用 4 个 Nvidia Titan Xp GPU 进行训练，大约需要一天时间才能收敛。请注意，由于所提出网络的所有层都是卷积的，因此输入的退化图像（degraded image）可以是任意大小。

V. EXPERIMENTAL RESULTS

在本节中，我们执行几个 IR 任务来验证所提出网络的性能，包括图像去噪、去模糊和超分辨率。我们针对不同的 IR 任务训练了每个模型。我们凭经验发现，在网络中实现算法 1 的 T = 6 次迭代通常会导致图像去噪、去模糊和超分辨率任务的满意 IR 结果。因此，我们为所有 IR 任务固定了 T = 6。为了训练网络，我们构建了一个大型训练图像集，由 [18] 中使用的 1000 张大小为 256 × 256 的图像组成。

A. Ablation study

为了展示退化矩阵 A 初始化的效果，我们使用两种类型的初始化来实现所提出的网络，即使用退化矩阵 A（表示为 DPDNN-A）和随机初始化（表示为作为 DPDNN-Random）。表 I 显示了这项比较研究。对于图像超分辨率，当我们使用双三次下采样的 SR 的双三次插值函数实现退化矩阵 A 时，我们只展示了使用高斯下采样的图像 SR 的消融研究。从表一可以看出，对于图像去模糊和 SR 任务，这两种初始化导致相似的结果，表明网络可以从零开始学习与退化矩阵相关的线性层。

我们还对降噪器初始化的影响进行了消融研究，即使用预先训练的降噪器（表示为 DPDNN-Pretrain）或随机初始化的降噪器（表示为 DPDNN-Random）来实现所提出的网络。总共提取了 450, 000 个大小为 40×40 的块用于训练。 [0, 50] 范围内的噪声水平用于模拟噪声图像块。表 II~IV 分别显示了该方法对图像去噪、SR 和去模糊任务的平均 PSNR 结果。从表 II~IV 中，我们可以看到降噪器的两次初始化也导致了相似的结果。上述两项消融研究表明，所提出的网络对参数的初始化不敏感。原因是网络参数的数量是可控的，因为我们强制每个降噪器共享相同的参数，因此可以有效地从头开始学习网络。

为了展示加入退化模型的效果，我们还训练了用于图像去模糊和 SR 的去噪网络。去噪网络的结构如图1(b) 所示。我们将去噪网络（表示为 Den-network）与提出的 DPDNN 进行了图像去模糊和 SR 的比较。比较结果如表Ⅴ～Ⅵ所示。从表 V~VI 中，我们可以看到所提出的 DPDNN 方法比去噪网络表现得更好。对于图像去模糊和 SR，去噪网络的平均 PSNR 增益可分别高达 0.42 dB 和 0.63 dB，展示了将退化模型纳入网络的优势。

B. Image denoising

对于图像去噪，A = I 和算法 1 简化为迭代去噪过程，即将加权噪声图像添加回去噪图像以进行下一个去噪过程。这种迭代去噪已经显示出对仅去噪一次的传统去噪方法的改进[14]。在这里，我们还发现在所提出的网络中实施多次去噪迭代可以改善去噪结果。为了训练网络，我们从训练图像中提取大小为 40 × 40 的图像块，并将加性高斯噪声添加到提取的块中以生成噪声块。总共 N = 450, 000 个补丁被提取用于训练。请注意，没有任何测试图像包含在训练图像集中。训练补丁也通过翻转和旋转来增强。我们将所提出的网络与几种领先的去噪方法进行了比较，包括三种基于模型的去噪方法，即 BM3D 方法 [10]、EPLL 方法 [66] 和基于低秩的方法 WNNM 方法 [15]，以及三种深度基于学习的方法，即 TNRD 方法 [9]、DnCNN-S 方法 [63] 和 MemNet [50]。

表 VII 显示了竞争方法在图 2 所示的一组常用测试图像上的 PSNR 结果。可以看出，MemNet 方法在低噪声水平上与 DnCNN-S 方法的性能相当，在低噪声水平上优于 DnCNN-S更高的噪音水平。所提出的网络平均比 MemNet 方法略好 0.2 dB。为了进一步验证所提出方法的有效性，我们还使用包含 68 张自然图像的伯克利分割数据集（BSD68）进行比较研究。表 VIII 显示了 BSD68 上测试方法的平均 PSNR 和 SSIM 结果。可以看出，对于更高的噪声水平，PSNR 增益相对于其他测试方法变得更大。所提出的方法在 BSD68 上平均优于 MemNet 方法高达 0.65 dB，证明了所提出方法的有效性。测试方法得到的部分去噪图像如图 3-4 所示。可以看到，通过基于模型的方法（即 BM3D、WNNM 和 EPLL）恢复的图像边缘和纹理是过度平滑的。基于深度学习的方法 TNRD、DnCNN-S、MemNet 和所提出的方法产生了视觉上更令人愉悦的图像结构。此外，所提出的方法在恢复图像细节方面比 TNRD、DnCNN-S 和 MemNet 方法产生了更好的结果。

C. Image deblurring

为了训练所提出的图像去模糊网络，我们首先将训练图像与模糊核进行卷积以生成模糊图像，然后从模糊图像中提取大小为 120 × 120 的训练图像块。标准差 σn 的加性高斯噪声也被添加到模糊图像中。采用了带有翻转和旋转的补丁增强，总共生成了 450, 000 个补丁用于训练。考虑了两种类型的模糊内核，即标准差为 1.6 的 25 × 25 高斯模糊内核和 [33] 中采用的大小为 19 × 19 和 17 × 17 的两个运动模糊内核。我们针对不同的模糊设置训练了每个模型。我们将所提出的方法与几种领先的去模糊方法进行了比较，即三种领先的基于模型的去模糊方法（EPLL [66]、IDDBM3D [11] 和 NCSR [19]）和当前最先进的基于去噪的去模糊CNN降噪器[64]（表示为DD-CNN）的方法。我们还与 MemNet [50] 方法进行了比较。我们使用成对的模糊图像块和原始图像块来训练 MemNet。为了公平比较，提出的网络和 MemNet 都使用了相同的训练图像块。本次比较研究中涉及的测试图像如图5所示。在本实验中，我们只对灰度图像进行反卷积。然而，所提出的方法可以很容易地扩展到彩色图像去模糊。

表 IX 中报告了测试去模糊方法的 PSNR 结果。为了公平比较，其他方法（MemNet除外）的所有PSNR都是由作者发布的代码生成或直接根据他们的论文编写的。从表 IX 中，我们可以看到 MemNet 方法的性能比传统的基于模型的 EPLL、IDDBM3D 和 NCSR 方法好得多。所提出的方法平均优于 MemNet 方法高达 0.44 dB。对于具有较高噪声水平的运动模糊内核，所提出的方法比 DD-CNN 方法稍差，后者需要更多的迭代（最多 30 次迭代）才能获得满意的结果。竞争方法的部分去模糊图像显示在图 6-8 中。从图 6-8 可以看出，所提出的方法不仅产生了更锐利的边缘，而且恢复了比其他方法更多的细节。

D. Image super-resolution

对于图像超分辨率，我们考虑两个图像子采样算子，即双三次下采样和高斯下采样。对于前一种情况，通过应用缩放因子为 1/s (s = 2, 3, 4) 的双三次插值函数对 HR 图像进行下采样，以模拟 LR 图像。对于后一种情况，LR 图像是通过将高斯模糊核应用于原始图像然后进行二次采样来生成的。在这种情况下，使用标准差为 1.6 的 7 × 7 高斯模糊核。 LR/HR 补丁对从 LR/HR 训练图像对中提取，并通过翻转和旋转进行增强，生成 450、000 个补丁对。 LR 补丁大小为 32 × 32，而 HR 补丁大小为 (32 * s) × (32 * s)。我们针对两个下采样案例训练每个网络。采用图像SR文献中常用的图像数据集进行性能验证，包括Set5、Set14、BSD100和包含100张高质量图像的Urban100数据集[27]。我们将所提出的方法与几种领先的图像 SR 方法进行了比较，包括两种基于 DCNN 的 SR 方法（SRCNN [12]、VDSR [27] 和 MemNet [50]）和两种去噪方法（TNRD [9] 和 DnCNN [63]），它通过首先使用双三次插值器对 LR 图像进行上采样，然后对上采样图像进行去噪以恢复高频细节来生成 HR 图像。为了公平比较，其他人的结果直接从他们的论文中借用或由作者发布的代码生成。

表 X 中报告了双三次下采样测试方法的 PSNR 结果。从表 X 中，我们可以看到所提出的方法和 MemNet 方法在 Set5 上平均优于其他方法。对于该数据集，MemNet 方法平均略好于建议的方法。如表 X 所示，平均而言，所提出的方法略优于 MemNet，这是该对照组中第二好的方法。表 XI 中报告了使用比例因子 3 进行高斯下采样的测试方法的 PSNR 结果。对于这种情况，我们将所提出的方法与 DD-CNN [64] 进行比较，它可以取得比他们早期的 DnCNN [63] 更好的结果。我们还与 MemNet 方法进行了比较 [50]。为了公平比较，我们还使用 LR 图像块和相应的 HR 图像块对重新训练 MemNet 模型。从表 XI 中，我们可以看到所提出的方法比 MemNet 方法有更大的优势。所提出的方法还优于使用预训练 DCNN 降噪器的迭代 DD-CNN 方法。测试方法重建的部分HR图像如图9-11所示，从中可以看出，所提出的方法可以产生比其他方法更清晰的边缘。

E. Complexity anlaysis

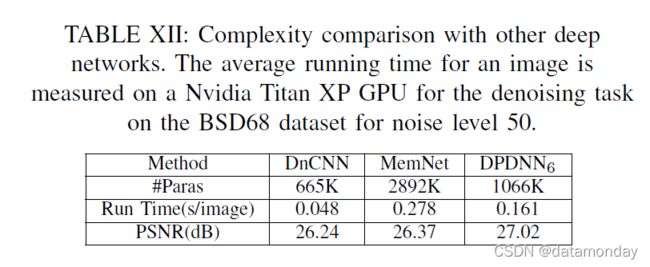
我们在复杂性方面将所提出的网络与其他两种基于深度学习的最先进的 IR 方法（即 DnCNN [63] 和 MemNet [50]）进行了比较。每个深度网络的参数数量如表 XII 所示。从表 XII 中，我们可以看到 MemNet 包含的参数数量最多，几乎是建议网络的三倍，因为它非常深（最多 80 层）。

由于我们强制每个降噪器共享相同的参数，因此建议网络的参数总数远小于 MemNet。虽然提出的网络有 L = 6 个阶段，但提出的网络的运行时间也小于 MemNet。这是因为降噪器中的特征图被逐渐下采样。因此，计算复杂度可以大大降低。

VI. CONCLUSION

在本文中，我们提出了一种用于一般图像恢复 (IR) 任务的新型深度神经网络。与当前基于深度网络的 IR 方法通常忽略观察模型不同，我们基于基于去噪的 IR 框架构建深度网络。为此，我们首先开发了一种有效的算法来解决基于去噪的 IR 方法，然后将该算法展开为一个深度网络，该深度网络由多个去噪模块（ denoising modules）与反投影模块（ denoising modules）交错组成，以实现数据一致性。开发了一种利用自然图像多尺度冗余的基于 DCNN 的降噪器。因此，所提出的深度网络不仅可以利用有效的 DCNN 去噪先验，还可以利用观察模型的先验。实验结果表明，所提出的方法可以在包括图像去噪、去模糊和超分辨率在内的几个 IR 任务上实现非常有竞争力且通常是最先进的结果。

---

Torch Code

# paper name "Denoising Prior Driven Deep Neural Network for Image Restoration "
# Code implementation by PyTorch

import numpy as np
import torch
import torch.nn as nn


class DPDNN(nn.Module):
    def __init__(self):
        super(DPDNN, self).__init__()

        # input channel = 1
        # Feature_Encoder contains four convolution layers, only the last layer halves the size of the feature map
        self.Feature_Encoder1_fe = nn.Sequential(
            nn.Conv2d(1, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU())
        self.Feature_Encoder1_down = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU())

        self.Feature_Encoder2_fe = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU())
        self.Feature_Encoder2_down = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU())

        self.Feature_Encoder3_fe = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU())
        self.Feature_Encoder3_down = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU())

        self.Feature_Encoder4_fe = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU())
        self.Feature_Encoder4_down = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1, stride=2), nn.ReLU())

        self.encoder_end = nn.Sequential(
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU())

        # Feature_Decoder contains five convolution layers, only the first layer doubles the size of the feature map
        self.decoder_up4 = nn.ConvTranspose2d(64, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.Feature_Decoder4 = nn.Sequential(
            nn.Conv2d(128, 64, 1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1))

        self.decoder_up3 = nn.ConvTranspose2d(64, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.Feature_Decoder3 = nn.Sequential(
            nn.Conv2d(128, 64, 1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1))

        self.decoder_up2 = nn.ConvTranspose2d(64, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.Feature_Decoder2 = nn.Sequential(
            nn.Conv2d(128, 64, 1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1))

        self.decoder_up1 = nn.ConvTranspose2d(64, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.Feature_Decoder1 = nn.Sequential(
            nn.Conv2d(128, 64, 1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1), nn.ReLU(),
            nn.Conv2d(64, 64, 3, padding=1))

        self.Feature_Decoder_end = nn.Conv2d(64, 1, 3, padding=1)

        # Defining learnable parameters
        self.delta_1 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_1 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.delta_2 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_2 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.delta_3 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_3 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.delta_4 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_4 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.delta_5 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_5 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.delta_6 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)
        self.eta_6 = nn.Parameter(torch.FloatTensor(1), requires_grad=True)

        # delta and eta were empirically initialized as 0.1 and 0.9, respectively
        self.delta_1.data = torch.tensor(0.1)
        self.eta_1.data = torch.tensor(0.9)
        self.delta_2.data = torch.tensor(0.1)
        self.eta_2.data = torch.tensor(0.9)
        self.delta_3.data = torch.tensor(0.1)
        self.eta_3.data = torch.tensor(0.9)
        self.delta_4.data = torch.tensor(0.1)
        self.eta_4.data = torch.tensor(0.9)
        self.delta_5.data = torch.tensor(0.1)
        self.eta_5.data = torch.tensor(0.9)
        self.delta_6.data = torch.tensor(0.1)
        self.eta_6.data = torch.tensor(0.9)

    # define model
    def forward(self, input):
        x = input
        y = input

        for i in range(6):
            f1 = self.Feature_Encoder1_fe(x)
            down1 = self.Feature_Encoder1_down(f1)

            f2 = self.Feature_Encoder2_fe(down1)
            down2 = self.Feature_Encoder2_down(f2)

            f3 = self.Feature_Encoder3_fe(down2)
            down3 = self.Feature_Encoder1_down(f3)

            f4 = self.Feature_Encoder4_fe(down3)
            down4 = self.Feature_Encoder2_down(f4)

            media_end = self.encoder_end(down4)

            # print(media_end.size())

            up4 = self.decoder_up4(media_end)
            concat4 = torch.cat([up4, f4], dim=1)
            decoder4 = self.Feature_Decoder4(concat4)

            up3 = self.decoder_up3(decoder4)
            concat3 = torch.cat([up3, f3], dim=1)
            decoder3 = self.Feature_Decoder3(concat3)

            up2 = self.decoder_up2(decoder3)
            concat2 = torch.cat([up2, f2], dim=1)
            decoder2 = self.Feature_Decoder2(concat2)

            up1 = self.decoder_up1(decoder2)
            concat1 = torch.cat([up1, f1], dim=1)
            decoder1 = self.Feature_Decoder1(concat1)

            v = self.Feature_Decoder_end(decoder1)

            v = v + x

            x = self.reconnect(v, x, y, i)

        return x

    def reconnect(self, v, x, y, i):

        i = i + 1
        if i == 1:
            delta = self.delta_1
            eta = self.eta_1
        if i == 2:
            delta = self.delta_2
            eta = self.eta_2
        if i == 3:
            delta = self.delta_3
            eta = self.eta_3
        if i == 4:
            delta = self.delta_4
            eta = self.eta_4
        if i == 5:
            delta = self.delta_5
            eta = self.eta_5
        if i == 6:
            delta = self.delta_6
            eta = self.eta_6

        recon = torch.mul((1 - delta - eta), v) + torch.mul(eta, x) + torch.mul(delta, y)

        return recon


if __name__ == '__main__':

    input1 = torch.rand(1, 1, 128, 128)

    net = DPDNN()

    out = net(input1)
    # print(net)
    print(out.size())