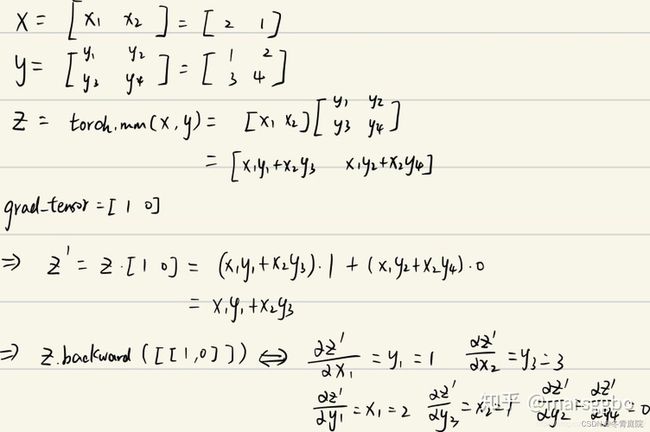动手学深度学习笔记第四章(多层感知器)
4.1 多层感知器
- y.backward(torch.ones_like(x),retain_graph=True)这里的retain_graph=True参数:pytorch进行一次backward之后,各个节点的值会清除,这样进行第二次backward会报错,因为虽然计算节点数值保存了,但是计算图结构被释放了,如果加上retain_graph==True后,可以再来一次backward。
- 关于detach:众所周知detach的作用就是把变量从计算图中扣掉,之后requires_grad就为false了,但是有点需要注意,z=x.detach()之后x本身还是可以向后传播的,z和x.detach()都是不能向后传播的,见下例:
z=x.detach()
print(z.requires_grad)
print(x.requires_grad)
print(x.detach().requires_grad)
False
True
False
- 对torch求导的新认识:如果需要计算导数,可以在 Tensor 上调用 .backward()。如果 Tensor 是一个标量(即它包含一个元素的数据),则不需要为 backward() 指定任何参数,但是如果它有更多的元素(是矩阵),则需要指定一个 gradient 参数,该参数是形状匹配的张量。这里引用这篇博客的例子。
x = torch.ones(2,requires_grad=True)
print(x)
z = x + 2
print(z)
z.backward()
print(x.grad)
# 出现grad can be implicitly created only for scalar outputs
# 因为此时的y并不是一个标量(即它包含一个元素的数据)
# 意思是只有对标量输出它才会计算梯度,而求一个矩阵对另一矩阵的导数束手无策。
RuntimeError: grad can be implicitly created only for scalar outputs
x = torch.ones(2,requires_grad=True)
z = x + 2
z.sum().backward()#或者z.backward(torch.ones_like(x))
print(x.grad)
>>> tensor([1., 1.])
如果不是对应矩阵的单位向量也是可以的,但是计算导数会发生变化:
x = torch.tensor([2., 1.], requires_grad=True)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)
z = torch.mm(x.view(1, 2), y)
print(f"z:{z}")
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")
>>> z:tensor([[5., 8.]], grad_fn=<MmBackward>)
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],
[1., 0.]])
4.3 多层感知器的简洁实现
- net.apply(fn):这个apply函数会将net里面的子模块(也就是网络)调用fn函数,然后再对net本身调用fn函数。如果想要针对里面的某个特定的模块调用函数可以加入type(m) == nn.Linear:这类判断语句,从而对子模块m进行处理,例子如下:
net=nn.Sequential(nn.Flatten(),
nn.Linear(784,256),
nn.ReLU(),
nn.Linear(256,10))
def init_weights(m):
if type(m)==nn.Linear:
nn.init.normal_(m.weight,std=0.01)
net.apply(init_weights)
4.4 模型选择与过拟合、欠拟合
- np.power的使用:如果是两个标量很简单,就是求次方。如果是两个列表,那么就是对应位置求次方。如果是两个矩阵,需要广播就先广播,然后进行对应元素求平方。
a=np.arange(3).reshape(-1,1)
b=np.arange(10).reshape(1,-1)
print(a)
print(b)
np.power(a,b)
[[0]
[1]
[2]]
[[0 1 2 3 4 5 6 7 8 9]]
array([[ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 1, 2, 4, 8, 16, 32, 64, 128, 256, 512]], dtype=int32)
- np.dot的使用:分为多维与多维、标量与多维、标量与标量、多维与一维几种情况。
a=np.array([1,2,3,4,5])
b=np.arange(10).reshape(2,5)
print(a)
print(b)
print(np.dot(b,a))#多维(>2)数组与0维数组(标量)做dot操作,相当于每一行对应元素相乘再求和,但是注意这里的顺序不能错了,dot(b,a)
[1 2 3 4 5]
[[0 1 2 3 4]
[5 6 7 8 9]]
[ 40 115]
c=np.arange(5).reshape(5,1)
print(c)
print(np.dot(b,c))#多维(>2)数组与二维数组(注意这里不是标量),进行dot相当于矩阵乘法
[[0]
[1]
[2]
[3]
[4]]
[[30]
[80]]
d=np.arange(10).reshape(5,2)
print(d)
print(np.dot(d,b))#多维矩阵的dot相当于矩阵乘法
[[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
[[ 5 6 7 8 9]
[ 15 20 25 30 35]
[ 25 34 43 52 61]
[ 35 48 61 74 87]
[ 45 62 79 96 113]]
e=[1,2,3,4,5]
f=[1,2,3,4,5]
np.dot(e,f)#标量(可以是列表)的dot操作是直接点乘求和
55
权重衰退
- torch.matmul()用法:(1)是1维*1维(两个标量),结果为向量内积:
tensor1 = torch.Tensor([1,2,3])
tensor2 =torch.Tensor([4,5,6])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())
tensor1 : tensor([1., 2., 3.])
tensor2 : tensor([4., 5., 6.])
ans : tensor(32.)
ans.size : torch.Size([])
(2)二维*二维:就是矩阵乘法运算
(3)二维*一维:结果是矩阵向量积
tensor1 =torch.Tensor([[4,5,6],[7,8,9]])
tensor2 = torch.Tensor([1,2,3])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())
tensor1 : tensor([[4., 5., 6.],
[7., 8., 9.]])
tensor2 : tensor([1., 2., 3.])
ans : tensor([32., 50.])
ans.size : torch.Size([2])
简单理解就是每一行都乘以那个1维的向量然后求和,最后组成一个一维的向量。
(4)一维*二维:开始变成 1 * m(一维的维度),也就是一个二维, 再进行正常的矩阵运算, 然后再去掉开始增加的一个维度
tensor1 = torch.Tensor([1,2,3]) # 注意这里是一维
tensor2 =torch.Tensor([[4,5],[4,5],[4,5]])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())
tensor1 : tensor([1., 2., 3.])
tensor2 : tensor([[4., 5.],
[4., 5.],
[4., 5.]])
ans : tensor([24., 30.])
ans.size : torch.Size([2])
- torch.norm():求范数,默认是L2范数
a = torch.ones((2,3)) #建立tensor
a2 = torch.norm(a) #默认求2范数
a1 = torch.norm(a,p=1) #指定求1范数
print(a)
print(a2)
print(a1)
tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor(2.4495)
tensor(6.)
- python中的item函数:item()函数的作用是从包含单个元素的张量中取出该元素值,并保持该元素的类型不变。
- 关于train_epoch_ch3函数接受的loss的问题:内置的loss求出来的是张量,所以需要进行mean或者sum,如果是pytorch自带的updater优化器,那么它是不会再updater里面对loss求均值,所以后面需要l.mean().backward();而d2l自己写的updater优化器里面用的sgd,已经对loss求过平均了,所以后面就是l.sum().backward()
- 关于为什么权重值减少可以降低过拟合或者噪声干扰的效果:我们首先想,权重小到极致,为0,就相当于减少了参数的个数,模型变简单了肯定防止了过拟合,但是我们又不希望这么大的力度,因为这样可能会导致模型欠拟合,所以调整权重值小一点,但是又不用小到0,就相当于削减了那些参数的作用但是也没有完全不用那些参数,在函数图上面展现的就是曲线更加平滑了。
- nn.MSELoss(reduction=‘none’):
(1)当reduce=True时,若size_average=True,则返回一个batch中所有样本损失的均值,结果为标量。
(2)当reduce=True时,若size_average=False,则返回一个batch中所有样本损失的和,结果为标量。
(3)当reduce=False时,则size_average参数失效,即无论size_average参数为False还是True,效果都是一样的。此时,函数返回的是一个batch中每个样本的损失,结果为向量。
(4)reduction参数包含了reduce和size_average参数的双重含义。即,当reduction=‘none’时,相当于reduce=False;当reduction=‘sum’时,相当于reduce=True且size_average=False;当reduction=‘mean’时,相当于reduce=True且size_average=True; - 关于torch.optim.SGD()的传参问题:有两种使用方式:
trainer=torch.optim.SGD([
{"params":net[0].weight,'weight_decay':2},
{"params":net[0].bias}],lr=lr)
trainer=torch.optim.SGD(net[0].parameters,lr=lr,weight_decay=2)
两种都是可以的,因为SGD的参数params是可迭代的:

也就是说传入的参数只要是列表并且列表中要是dict类型的,这样定义好哪个参数是哪个或者net.parameters()出来的generator都可以的,都可以使用for循环来进行迭代。
- python和pytorch中的矩阵乘法:参考
python:
(1) np.dot() 或 **@**对于两种数据格式均为矩阵乘法
(2) np.multiple() 对于两种数据格式均为按对应位置元素相乘
(3) * 对于 array 是按元素相乘,对于mat是做矩阵乘法
a = np.array([[1., 2.], [3., 4.]])
b = np.array([[1., 2.], [3., 4.]])
# 对应位置元素做乘法
c_1 = a * b
[[ 1. 4.]
[ 9. 16.]]
# 线性代数中常规的矩阵乘法
c_2 = np.dot(a, b) # 等价于 a @ b
[[ 7. 10.]
[15. 22.]]
# 对应位置元素做乘法
c_3 = np.multiply(a, b)
[[ 1. 4.]
[ 9. 16.]]
a = np.mat([[1., 2.], [3., 4.]])
b = np.mat([[1., 2.], [3., 4.]])
# 线性代数中常规的矩阵乘法
c_1 = a * b
[[ 7. 10.]
[15. 22.]]
# 线性代数中常规的矩阵乘法
c_2 = np.dot(a, b)
[[ 7. 10.]
[15. 22.]]
# 对应位置元素做乘法
c_3 = np.multiply(a, b)
[[ 1. 4.]
[ 9. 16.]]
pytorch:
(1) torch.mul(a, b)(与*相等)
可以广播, 是矩阵a和b 对应位相乘,a和b的维度必须相等,比如a的维度是(1, 2),b的维度是(1, 2),返回的仍是(1, 2)的矩阵;或者a和b的行向量数目是一样的就可以广播了。
(2) torch.mm(a, b)
是矩阵a和b矩阵相乘,比如a的维度是(1, 2),b的维度是(2, 3),返回的就是(1, 3)的矩阵。只能处理二维矩阵
(3) torch.matmul() 能处理batch、广播的矩阵,等价于使用 @
当输入是一维和一维时,结果是对应元素相乘再求和
当输入是二维时,和 torch.mm 函数用法相同
当输入是多维时,把多出的一维(第一维)作为batch提出来,其他部分做矩阵乘法
当输入是向量(一维)和n维(n>2),将向量增加一个维度相当于列向量,然后与多维矩阵乘法,结果的维度是n-1
例子:
a = torch.tensor([[1., 2.], [3., 4.]])
b = torch.tensor([[1., 2.], [3., 4.]])
c_1 = torch.mm(a, b)
tensor([[ 7., 10.],
[15., 22.]])
c_2 = torch.mul(a, b)
tensor([[ 1., 4.],
[ 9., 16.]])
a = torch.ones((5, 3, 4))
b = torch.ones((4, 2))
c = torch.matmul(a, b)
print(c.shape)
torch.Size([5, 3, 2])
a = torch.ones((2, 3, 4))
b = torch.ones((1, 4, 2))
c = torch.matmul(a, b)
print(c.shape)
torch.Size([2, 3, 2])
a = torch.ones((2, 1, 3, 4))
b = torch.ones((1, 4, 2))
c = torch.matmul(a, b) # 等价于 c = a @ b
print(c.shape)
torch.Size([2, 1, 3, 2])
x = torch.tensor([1, 2, 3])
y = torch.tensor([[
[7, 8],
[9, 10],
[11,12]
]])
torch.matmul(x,y)
tensor([[58, 64]])
- dropout丢弃的神经元,反向传播的时候相关的权重也不会得到更新,也就是梯度再反向传播的时候也会消失,因为:

- super(Net, self).__init__() :这里的意思是继承mro列表Net后面一个父类。super有个内核叫做mro,是method resolution order的缩写,作用是,mro会记录一个父类列表,告诉self实例所属的这个类在继承过程中,究竟调用哪一个父类的__init__()方法来初始化,免得父类直接相互有继承关系而造成__init__()方法交叉调用的混乱。
class Son(Father1, Father2):
def __init__(self):
super(Son, self).__init__()
mro列表=[Son, Father1, Father2, Base],super会从mro中,找到传入它的第一个参数’Son’,并第一个参数’Son’右边的一个类开始,依次寻找__init__函数。这里是从Father1开始寻找,一旦找到,就把找到的__init__函数绑定到self对象,并返回。如果想继承中调用Father2的__init__()方法,就应该写成:
class Son(Father1, Father2):
def __init__(self):
super(Father1, self).__init__()
- 导数公式的推导:


- Xavier初始化理解:为了让梯度有个合理的范围(不能nan也不能inf),我们可以让forward和backward每一层的输入输出都满足均值为0、方差为一个常数的条件,这样就可以相当于把值限定在了一个范围内,并且不太可能有太大的变化。原因是大多数最优解附近都是平坦的,梯度变化都不会太大。而Xavier就是通过让初始化的权重参数满足均值为0,方差为一个数学公式推出的常熟的分布,可以让forward和backward近似满足均值为0、方差为一个常数的条件的。
而为什么不用担心梯度消失,我的理解是消失一般的原因是激活函数导致的,所以这地方的操作应该不会导致。 - 梯度消失的结果是参数更新不动,也就是学不动了;梯度爆炸可能会导致中间层特征值nan也有可能inf。
- 矩阵求导前后维度一般不变,这里是为了能够计算矩阵乘法,所以要转置,相关推导见这里

- 分布偏移:训练集和测试集并不来自同一个分布。分为协变量偏移、标签偏移和概念偏移。
协变量偏移:测试集的协变量X的分布发生了变化,比如我们要探究抽烟习惯 对5年内肺癌发病率 的影响,在我们做实验的过程中,政府颁布了关于公共场所禁止吸烟的法案,法案的提出对人群中吸烟习惯 的统计分布有很大的影响。
标签偏移:测试集的因变量Y的分布发生了变化,比如垃圾邮件的分类,很可能在实际场景中邮件样本绝大多数都是垃圾邮件,只有少部分不是垃圾邮件,但是我们的训练集的数据类别占比是50%,50%。
概念偏移:意思是我们的目标发生了改变,也就是X和Y之间对应的目标函数发生了改变,比如在水处理系统的传感器时间序列异常检测中,因为上游放水,一段维持较高水位,但是并不能和其余时间一样被认定为是报警事件,也就是说这个时候的模型需要进行调整更换。 - python函数return返回的数如果没有加括号,只是简单的逗号分隔,那么返回的类型是元组,而后续要将返回的值作为参数传入函数就需要进行解包。
# 元组-可以包含多个数据,因此可以使用元组让函数一次返回多个值
# 如果函数返回的类型是元组,小括号可以省略
# return (temp, wetness)
return temp, wetness # 小括号可以省略
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size) #这里的data就解包了
- K折交叉验证:主要目的是为了调超参数,因为不用K折的话,很可能当前的超参数只适用于当前的划分方式,泛化能力不够好。调好超参数之后,就可以用这个超参数的网络来训练整个数据(验证集也加进训练集),用在测试集上出结果了。
- pandas的concat:
all_features=pd.concat((train_data.iloc[:,1:-1],test_data.iloc[:,1:]))#传参必须是列表或者元组这种iterable类型
print(type(all_features))
<class 'pandas.core.frame.DataFrame'>
- 对pandas的dataframe操作的时候,左边一定要写原先要操作的数然后等于后面要操作的,不然操作完不会保存。
numeric_features=all_features.dtypes[all_features.dtypes!='object'].index
all_features[numeric_features]=all_features[numeric_features].apply(lambda x:(x-x.mean())/(x.std()))
all_features[numeric_features]=all_features[numeric_features].fillna(0)#注意这两行左边写all_features[numeric_features]的话没办法改进去
- 注意这里的对数误差函数的思想:我们在测试集判断模型好坏的时候依据的应该是相对数量而不是绝对数量,举个例子:我们一个模型预测的是250,实际是300,另一个模型预测的10,实际是20,那么肯定是第一个模型更好,但是第一个模型的误差数却更大,所以我们用取对数的办法近似关注相对数量。但是我们训练的时候,就没必要取对数了,因为虽然相对数量不大,但是我们所学习的目的是缩小差距,所以绝对数量大就说明我们移动的距离就要更大,如果改用相对距离就会每次动的很少了。
def log_rmse(net, features, labels):
clipped_preds = torch.clamp(net(features),1,float('inf')) # 把模型输出的值限制在1和inf之间,inf代表无穷大(infinity的缩写)
rmse = torch.sqrt(loss(torch.log(clipped_preds),torch.log(labels))) # 预测做log,label做log,然后丢到MSE损失函数里
return rmse.item()
- 关于pd.Series(preds.reshape(1,-1)[0]的疑惑:
test_data['SalePrice']=pd.Series(preds.reshape(1,-1)[0])#这里意思是先将preds变为一行的二维数组再取第一行元素出来,取得就是一维的了,才能变成Series类型
s=np.array([1,2,3,4,5]).reshape(1,-1)
print(s)
s=np.array([1,2,3,4,5]).reshape(1,-1)[0]
print(s)
[[1 2 3 4 5]]
[1 2 3 4 5]