因子图原理推导及Gtsam简要使用说明
因子图推导及Gtsam简要使用说明
参考链接:
Theory, Programming, and Applications of Factor Graph, Jing Dong;
Gtsam学习笔记——三川小哥;
因子图原理推导
因子图建模
下图为一个简单SLAM文件的抽象。蓝色三角形表示世界中被观测的路标点,黄色五边形为各个时刻的机器人姿态。红色箭头与绿色箭头分别为路标点观测与相邻位置姿态变换观测。

将上述简单SLAM问题表述为贝叶斯单向图有以下形式。将位姿与观测均表示为变量形式。箭头表明了由姿态生成观测的因果关系。
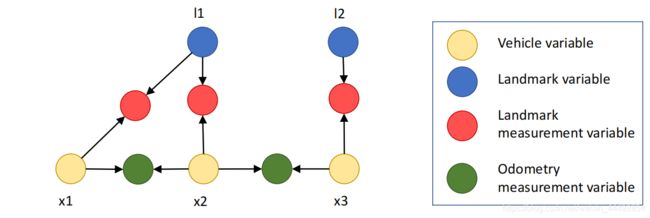
用 X X X表示位姿, Z Z Z表示观测,可以得出以下关系
P ( X , Z ) = P ( Z ∣ X ) P ( X ) P(X,Z)=P(Z|X)P(X) P(X,Z)=P(Z∣X)P(X)
位姿与观测的联合概率将由位姿的概率与已知位姿下的观测条件概率乘积获得。其中 P ( Z ∣ X ) P(Z|X) P(Z∣X)可展开为:
P ( Z ∣ X ) = ∏ i P i ( Z i ∣ X i ) = P ( z 11 ∣ l 1 , x 1 ) P ( z 12 ∣ l 1 , x 2 ) P ( z 13 ∣ l 2 , x 3 ) P ( z 21 ∣ x 1 , x 2 ) P ( z 22 ∣ x 2 , x 3 ) P(Z|X)=\prod_iP_i(Z_i|X_i)=P(z_{11}|l_1,x_1)P(z_{12}|l_1,x_2)P(z_{13}|l_2,x_3)P(z_{21}|x_1,x_2)P(z_{22}|x_2,x_3) P(Z∣X)=i∏Pi(Zi∣Xi)=P(z11∣l1,x1)P(z12∣l1,x2)P(z13∣l2,x3)P(z21∣x1,x2)P(z22∣x2,x3)
然而,我们的问题是求取已知观测量的情况下各点位姿的概率,即要求 P ( X ∣ Z ) P(X|Z) P(X∣Z)
P ( X ∣ Z ) = P ( Z ∣ X ) P ( X ) P ( Z ) P(X|Z)=\frac{P(Z|X)P(X)}{P(Z)} P(X∣Z)=P(Z)P(Z∣X)P(X)
对于目标为求解X的该问题, P ( Z ) P(Z) P(Z)与问题无关,故可省略。
P ( Z ∣ X ) P ( X ) P ( Z ) ∝ P ( Z ∣ X ) P ( X ) \frac{P(Z|X)P(X)}{P(Z)}\varpropto P(Z|X)P(X) P(Z)P(Z∣X)P(X)∝P(Z∣X)P(X)
其中 P ( X ) P(X) P(X)表示的先验在实际问题中并不存在,故可暂时舍去。
由此,SLAM问题简化为了求取 X ∗ X^* X∗的极大似然概率问题,其中:
X ∗ = arg max x P ( Z ∣ X ) = arg max x ∏ i P i ( Z i ∣ X i ) X^*={\underset {x}{\operatorname {arg\,max}}}P(Z|X)={\underset {x}{\operatorname {arg\,max}}}\prod_iP_i(Z_i|X_i) X∗=xargmaxP(Z∣X)=xargmaxi∏Pi(Zi∣Xi)
将上式中每一个 P i ( Z i ∣ X i ) P_i(Z_i|X_i) Pi(Zi∣Xi)抽象为一个因子,将各个因子记为
ϕ i = ˙ ψ ( Z i , X i ) ∝ P i ( Z i ∣ X i ) \phi_i\dot{=}\psi(Z_i,X_i)\propto P_i(Z_i|X_i) ϕi=˙ψ(Zi,Xi)∝Pi(Zi∣Xi)
因此,问题可以进一步转化用因子表示的以下形式:
X ∗ = arg max x ∏ i P i ( Z i ∣ X i ) = arg max x ∏ i ϕ i X^*={\underset {x}{\operatorname {arg\,max}}}\prod_iP_i(Z_i|X_i)={\underset {x}{\operatorname {arg\,max}}}\prod_i\phi_i X∗=xargmaxi∏Pi(Zi∣Xi)=xargmaxi∏ϕi
因子图抽象为下图形式:
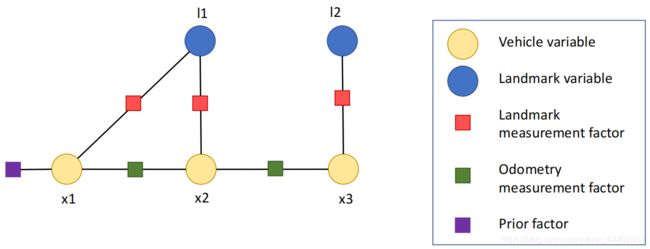
根据因子图进一步展开 ∏ i ϕ i \prod_i\phi_i ∏iϕi可以得到以下形式:
∏ i ϕ i = ˙ ϕ ( x 1 , l 1 ) ϕ ( x 2 , l 1 ) ϕ ( x 3 , l 2 ) ϕ ( x 1 , x 2 ) ϕ ( x 2 , x 3 ) ϕ ( x 1 ) \prod_i\phi_i\dot{=}\phi(x_1,l_1)\phi(x_2,l_1)\phi(x_3,l_2)\phi(x_1,x_2)\phi(x_2,x_3)\phi(x_1) i∏ϕi=˙ϕ(x1,l1)ϕ(x2,l1)ϕ(x3,l2)ϕ(x1,x2)ϕ(x2,x3)ϕ(x1)
其中:
ϕ ( x 1 , l 1 ) ϕ ( x 2 , l 1 ) ϕ ( x 3 , l 2 ) \phi(x_1,l_1)\phi(x_2,l_1)\phi(x_3,l_2) ϕ(x1,l1)ϕ(x2,l1)ϕ(x3,l2)为观测因子;
ϕ ( x 1 , x 2 ) ϕ ( x 2 , x 3 ) \phi(x_1,x_2)\phi(x_2,x_3) ϕ(x1,x2)ϕ(x2,x3)为里程计因子;
ϕ ( x 1 ) \phi(x_1) ϕ(x1)为先验因子。
因子图问题转化
对于每一个因子,都为其应用适当误差模型对齐进行建模。
使用最常见的高斯分布对其进行建模,则有:
ϕ i = e x p ( − 1 2 ∣ ∣ f i ∣ ∣ Σ 2 ) \phi_i=exp(-\frac{1}{2}||f_i||^2_\Sigma) ϕi=exp(−21∣∣fi∣∣Σ2)
对于不同因子类型,有不同的误差函数模型。
先验因子: f p r i o r ( x i ) = x i − z f_{prior}(x_i)=x_i-z fprior(xi)=xi−z
里程计因子: f o d o m e t r y ( x i , x i + 1 ) = ( x i + 1 − x i ) − z f_{odometry}(x_i,x_{i+1})=(x_{i+1}-x_i)-z fodometry(xi,xi+1)=(xi+1−xi)−z
观测因子: f l a n d m a r k ( x i , l j ) = p r o j e c t i o n ( x i , l j ) − z f_{landmark}(x_i,l_j)=projection(x_i,l_j)-z flandmark(xi,lj)=projection(xi,lj)−z
对于因子图问题进行对数化,可化简问题为:
X ∗ = arg max x ∏ i ϕ i = arg max x log ( ∏ i ϕ i ) = arg min x ∑ i ∣ ∣ f i ∣ ∣ Σ 2 X^*={\underset {x}{\operatorname {arg\,max}}}\prod_i\phi_i ={\underset {x}{\operatorname {arg\,max}}}\,\log(\prod_i\phi_i) ={\underset {x}{\operatorname {arg\,min}}}\sum_i||f_i||^2_\Sigma X∗=xargmaxi∏ϕi=xargmaxlog(i∏ϕi)=xargmini∑∣∣fi∣∣Σ2
至此,因子图问题可以转化为马氏距离(马氏范数)非线性最小二乘的形式。
接下来对上式进行线性化。
记所有因子的误差函数为统一格式:
f i = h i ( X i ) − z i f_i=h_i(X_i)-z_i fi=hi(Xi)−zi
式中:
h i ( X i ) h_i(X_i) hi(Xi)表示第i个因子的预测, z i z_i zi表示第i个因子的观测。
对各 h i ( X i ) h_i(X_i) hi(Xi)在各点附近进行一阶泰勒展开:
f i = h i ( X i ) − z i = h i ( X i 0 ) + J i Δ i − z i f_i=h_i(X_i)-z_i=h_i(X_i^0)+J_i\Delta_i-z_i fi=hi(Xi)−zi=hi(Xi0)+JiΔi−zi
其中:
雅可比矩阵 J i J_i Ji是在给定线性化点处 X i 0 X_i^0 Xi0对预测函数 h i ( ⋅ ) h_i(\cdot) hi(⋅)的多变量偏微分:
J i = ∂ h i ( X i ) ∂ X i ∣ X i 0 J_i=\frac{\partial h_i(X_i)}{\partial X_i}|_{X_i^0} Ji=∂Xi∂hi(Xi)∣Xi0
Δ i \Delta_i Δi表示为状态更新量:
Δ i = X i − X i 0 \Delta_i=X_i-X_i^0 Δi=Xi−Xi0
将泰勒展开后的因子误差函数带入因子图问题中:
X ∗ = arg min Δ ∑ i ∣ ∣ h i ( X i 0 ) + J i Δ i − z i ∣ ∣ Σ 2 = arg min Δ ∑ i ∣ ∣ J i Δ i − ( z i − h i ( X i 0 ) ) ∣ ∣ Σ 2 X^*={\underset {\Delta}{\operatorname {arg\,min}}}\sum_i||h_i(X_i^0)+J_i\Delta_i-z_i||^2_\Sigma ={\underset {\Delta}{\operatorname {arg\,min}}}\sum_i||J_i\Delta_i-(z_i-h_i(X_i^0))||^2_\Sigma X∗=Δargmini∑∣∣hi(Xi0)+JiΔi−zi∣∣Σ2=Δargmini∑∣∣JiΔi−(zi−hi(Xi0))∣∣Σ2
对于马氏范数到2范数有以下转化关系:
∣ ∣ e ∣ ∣ Σ 2 = e T Σ − 1 e = ( Σ − 0.5 e ) T ( Σ − 0.5 e ) = ∣ ∣ Σ − 0.5 e ∣ ∣ 2 2 ||e||_\Sigma^2=e^T\Sigma^{-1}e=(\Sigma^{-0.5}e)^T(\Sigma^{-0.5}e)=||\Sigma^{-0.5}e||_2^2 ∣∣e∣∣Σ2=eTΣ−1e=(Σ−0.5e)T(Σ−0.5e)=∣∣Σ−0.5e∣∣22
所以:
X ∗ = arg min Δ ∑ i ∣ ∣ Σ − 0.5 J i Δ i − Σ − 0.5 ( z i − h i ( X i 0 ) ) ∣ ∣ 2 2 X^*={\underset {\Delta}{\operatorname {arg\,min}}}\sum_i||\Sigma^{-0.5}J_i\Delta_i-\Sigma^{-0.5}(z_i-h_i(X_i^0))||^2_2 X∗=Δargmini∑∣∣Σ−0.5JiΔi−Σ−0.5(zi−hi(Xi0))∣∣22
记:
{ A i = Σ − 0.5 J i b i = Σ − 0.5 ( z i − h i ( X i 0 ) ) \begin{cases} A_i=\Sigma^{-0.5}J_i\\ b_i=\Sigma^{-0.5}(z_i-h_i(X_i^0)) \end{cases} {Ai=Σ−0.5Jibi=Σ−0.5(zi−hi(Xi0))
以上过程称为白化,通过该过程消去协方差矩阵。
则因子图问题转化为标准线性最小二乘问题:
X ∗ = arg min Δ ∑ i ∣ ∣ A i Δ i − b i ∣ ∣ 2 2 X^*={\underset {\Delta}{\operatorname {arg\,min}}}\sum_i||A_i\Delta_i-b_i||^2_2 X∗=Δargmini∑∣∣AiΔi−bi∣∣22
GtSAM使用简析
GtSAM 是目前因子图增量平滑方面成果的集成,其中囊括了从isam1到isam2、贝叶斯树的优化以及之后出现的流行优化等优化方法。无论是研究还是应用因子图优化,Gtsam都是不二之选。
以下示例以LOAM中的用法为例。
cmake引入
# 寻找第三方库,使用大小写都可以,这里列举了两种方式
find_package(Boost COMPONENTS thread filesystem date_time system REQUIRED)
FIND_PACKAGE(GTSAM REQUIRED)
# 包含第三方库头文件路径,可以使用绝对路径
INCLUDE_DIRECTORIES(${Boost_INCLUDE_DIR})
INCLUDE_DIRECTORIES(${GTSAM_INCLUDE_DIR})
INCLUDE_DIRECTORIES("/usr/include/eigen3")
add_executable(gtsam_test main.cpp)
# 链接库
target_link_libraries(gtsam_test ${Boost_LIBRARIES} -lgtsam -ltbb)
install(TARGETS gtsam_test RUNTIME DESTINATION bin)
因子图构建
创建因子图问题
//头文件
#include 因子图新增一元边
// 新增系统先验(首点因子,即一元边)
// PriorFactor<因子类型>(key因子编号,约束测量值,噪声)
gtSAMgraph.add(PriorFactor<Pose3>(0, Pose3(Rot3::RzRyRx(dRx, dRy, dRz),
Point3(dTransx, dTransy, dTransz)), priorNoise));
// 新增该因子优化初值
// initialEstimate.insert(key因子编号,位姿优化初值)
initialEstimate.insert(0, Pose3(Rot3::RzRyRx(dSumRx, dSumRy, dSumRz),
Point3(dSumTransx, dSumTransy, dSumTransz)));
因子图新增二元边
// 新增位姿约束(位姿之间,回环之间,即二元边)
// BetweenFactor<因子类型>(key因子编号1,key因子编号1,1-2的约束测量值,噪声)
gtSAMgraph.add(BetweenFactor<Pose3>(iKey1, iKey2,
poseFrom.between(poseTo), odometryNoise));
// 新增新出现因子的优化初值(绝对位姿)
// initialEstimate.insert(key因子编号,位姿优化初值)
initialEstimate.insert(iKey2,Pose3(Rot3::RzRyRx(dRx, dRy, dRz),
Point3(dTransx, dTransy, dTransz)));
因子图求解
// 每次新增因子后,进行优化问题更新
isam->update(gtSAMgraph, initialEstimate);
isam->update();
// 清空增量容器
gtSAMgraph.resize(0);
initialEstimate.clear();
// 优化问题求解
isamCurrentEstimate = isam->calculateEstimate();
// 获取优化结果
int numPoses = isamCurrentEstimate.size();
for (int i = 0; i < numPoses; ++i)
{
points[i].x = isamCurrentEstimate.at<Pose3>(i).translation().x();
points[i].y = isamCurrentEstimate.at<Pose3>(i).translation().y();
points[i].z = isamCurrentEstimate.at<Pose3>(i).translation().z();
points[i].roll = isamCurrentEstimate.at<Pose3>(i).rotation().roll();
points[i].pitch = isamCurrentEstimate.at<Pose3>(i).rotation().pitch();
points[i].yaw = isamCurrentEstimate.at<Pose3>(i).rotation().yaw();
}