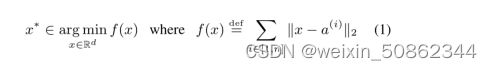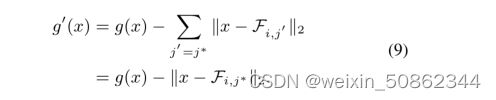【论文翻译】【剪枝】Filter Pruning via Geometric Medianfor Deep Convolutional Neural Networks Acceleration

目录

摘要

1.介绍

2.相关工作

 3. 方法

3.1 前置内容

3.2. 基于规范的准则分析

3.3. 真实场景中的Norm统计

3.4 通过几何中值进行过滤修剪

3.5. 理论和现实加速

3.5.1理论加速

3.5.2 实际加速

4.实验

4.1实验设置

4.2.单分支网络修剪

4.3.多分支网络修剪

4.4.消融研究

4.5.特征图可视化

5.结论和未来工作

---

摘要

以往的工作利用“小范数-不重要”准则修剪卷积神经网络中的小范数滤波器。在本文中，我们分析了这个基于范数的准则，并指出它的有效性取决于两个条件，而这两个条件并不总是被满足:(1)滤波器的范数偏差应该很大;(2)滤波器的最小范数应较小。为了解决这个问题，我们提出了一种新的滤波器剪枝方法，即几何中值滤波剪枝(FPGM)，不考虑这两个要求来压缩模型。与以前的方法不同，FPGM通过修剪冗余过滤器来压缩CNN模型，而不是那些“相对不那么重要”的过滤器。当应用于两个图像分类基准时，我们的方法验证了其有效性和优势。值得注意的是，在CIFAR-10上，FPGM在ResNet-110上降低了52%以上的FLOPs，相对精度提高了2.69%。此外，在ILSVRC2012上，FPGM在ResNet101上降低了42%以上的FLOPs，精度没有前5位的下降，这是先进的技术。代码可以在GitHub上公开获取:https://github.com/he-y/filter-pruning-geometric-median

1.介绍

 

图1。(a)基于范数的方法的剪枝准则和提出的方法的说明;(b)基于范数的滤波器剪枝准则要求。在(a)中，绿色方框表示网络的过滤器，其中较深的颜色表示滤波器的较大范数。对于基于范数的准则，只有范数最大的滤波器被保留，这是基于“小范数滤波器不那么重要”的假设。相比之下，该方法对网络中含有冗余信息的滤波器进行修剪。通过这种方式，可以保留由不同绿色强度表示的不同规范的过滤器。(b)中，蓝色曲线表示网络的理想范数分布，v1和v2分别为范数分布的最小值和最大值。要选择合适的阈值T(红色阴影)，需要达到两个要求，即范数偏差要大，范数的最小值要任意小。

        深度cnn的更深和更宽的架构带来了计算机视觉任务的卓越性能[6,26,45]。然而，它们也会导致高昂的计算成本，并使模型在移动设备上部署变得困难。即使是最新的高效架构，如残差连接[12]或inception 模块[34]，也有数百万个参数，需要数十亿个浮点运算[15]。因此，有必要获得计算成本相对较低但精度较高的深度CNN模型。

        最近关于剪枝的研究进展可以分为两类，即权重剪枝[11,1]和滤波剪枝[21,39]。权重修剪直接删除过滤器中的权重值，这可能会导致非结构化稀疏。这种不规则的结构使得利用高效的基本线性代数子程序(BLAS)库[25]变得很困难。相比之下，滤波修剪直接丢弃整个选择的过滤器，留下一个具有规则结构的模型。因此，滤波剪枝是加速网络和减小模型规模的首选方法。

        目前的实践[21,38,15]通过遵循“小范数-不重要”的标准来进行滤波器修剪，该标准认为具有较小范数的滤波器由于其重要性较低，可以安全地修剪。如图1(a)的右上方所示，在计算模型中滤波器的范数后，利用预先设定的阈值来选择范数小于 的滤波器。

        然而，如图1(b)所示，要使用这个“小规范-不重要”的标准，有两个先决条件。首先，滤波规范的偏差要显著。这一要求使得阈值的搜索空间足够宽，因此分离需要修剪的过滤器将是一项简单的任务。其次，可以修剪的滤波器的范数应该任意小，即接近于零;换句话说，对网络而言，具有较小规范的滤波器对网络的贡献绝对较小，而不是相对较小但具有较大的贡献的。当恰好满足这两个要求时，理想的范数分布如图1中的蓝色曲线所示。不幸的是，根据我们的分析和实验观察，这并不总是正确的。

        为了解决上述问题，我们提出了一种新的滤波器剪枝方法，称为几何中值滤波剪枝(FPGM)。与以往的方法不同，FPGM选择的是贡献相对较小的滤波器。具体来说，我们计算同一层内滤波器的几何中值(GM)[8]。根据GM的特性，它附近的滤波器F可以用剩下的滤波器表示。因此，修剪这些滤波器不会对模型性能产生实质性的负面影响。注意，FPGM不使用基于范数的准则来选择要修剪的过滤器，这意味着即使不能满足基于范数的准则的要求，其性能也不会下降。

        贡献。我们有三个贡献:

1)分析了以往工作中采用的基于范数的准则，剔除了相对不重要的滤波器。我们详细阐述了导致其局限性的两个基本要求;

(2)我们提出FPGM去修剪包含冗余信息的最可替换的滤波器，当基于范数的准则失效时，该滤波器仍能取得良好的性能;

(3)在两个基准上的大量实验证明了FPGM的有效性和效率。

2.相关工作

以往大多数关于加速cnn的工作大致可以分为四类，即矩阵分解[42,35]、低精度权值[44,43,32]、知识蒸馏[17,19]和剪枝。基于剪枝的方法旨在去除神经网络中不必要的连接[11,21,24]。从本质上讲，权重剪枝总是导致非结构化的模型，这使得难以部署高效的BLAS库，而滤波器剪枝不仅减少了设备上的存储占用，还减少了计算成本，从而加速推理。根据是否使用训练数据来确定剪枝滤波器，我们可以将滤波器剪枝方法大致分为两类，即数据依赖滤波器剪枝和数据独立滤波器剪枝。由于训练数据的使用需要大量的计算量，与数据无关的方法比数据相关的方法效率更高。

权重剪枝。最近的许多工作[11,10,9,36,1,15,41,4]都专注于修剪滤波器的细粒度权重。例如，[11]提出了一种迭代方法来丢弃值低于预定义阈值的小权重。[1]将修剪定义为一个优化问题，即在满足修剪成本条件的同时，找到使损失最小化的权重。

数据依赖滤波器剪枝。一些滤波器剪枝方法[23,25,16,27,7,33,39,37,46,14,18,22]需要利用训练数据来确定剪枝滤波器。[25]使用下一层的统计信息来指导筛选器的选择。[7]的目的是通过最小化训练集样本激活的重构误差来获得一个分解。[33]提出了一种固有的数据驱动方法，使用主成分分析(PCA)来指定应保留的能量的比例。[37]将子空间聚类应用于特征映射，以消除卷积滤波器中的冗余。

数据独立滤波器剪枝。与我们的工作同时，一些数据无关的过滤器修剪策略[21,15,38,47]已经被探索。[21]使用' 1范数标准修剪不重要的过滤器。[15]提出用' 2范数准则选择滤波器，并以软方式修剪这些滤波器。[38]提出通过对批归一化层的缩放参数强制稀疏性来修剪模型。[47]使用滤波器上的光谱聚类来选择不重要的。

讨论。据我们所知，以前只有一项工作重新考虑了更小的标准-更不重要的标准[38，Rethinking the
smaller-norm-less-informative assumption in channel pruning of convolution layers]。与此方法相比，我们想强调的优点如下:(1)[38]更注重批量归一化算子中缩放参数的稀疏性，这对没有批量归一化的结构并不友好。相反，我们的方法不受这种限制。(2)选择剪枝通道后，[38]需要进行微调以减少性能下降。然而，我们的方法将剪枝操作与正常的训练程序结合起来。因此，没有必要进行额外的微调。(3)[38]需要计算比例因子梯度;因此，大量的计算成本是不可避免的，而我们的方法可以在不计算比例因子梯度的情况下加速神经网络。

 

 3. 方法

3.1 前置内容

        在本小节中，我们正式介绍符号和符号。我们假设神经网络有L层。我们用和分别表示第i个卷积层的输入通道数和输出通道数。表示第i层的第j个滤波器，则滤波器的维数为，其中K为网络的核大小。网络W(i)的第i层可以用表示。深度CNN网络的连接张量可参数化为。

3.2. 基于规范的准则分析

        图1说明了成功利用基于规范的标准的两个需求。然而，这些要求可能并不总是成立，并且可能会导致意想不到的结果。具体如图2所示，其中蓝色虚线曲线和绿色实线曲线分别表示理想情况和实际情况下的正态分布。

 图2。基于范数的准则的理想与现实:(a)小范数偏差和(b)大最小范数。蓝色虚线曲线表示理想的正态分布，绿色实线曲线表示真实情况下可能出现的正态分布。

        (1)范数偏差小。如图2(a)所示，滤波器范数分布的偏差可能太小，这意味着范数集中在一个很小的区间内。范数偏差小导致搜索空间小，很难找到合适的阈值来选择要修剪的滤波器。

        (2)大最小范数。具有最小范数的滤波器不能任意小，如图2(b)， 。在这种情况下，那些被认为是最不重要的过滤器仍然对网络有很大的贡献，这意味着每个过滤器都具有很高的信息量。因此，用最小范数修剪这些滤波器会对网络产生负面影响。

3.3. 真实场景中的Norm统计

        在图3中，从CIFAR-10上预训练的ResNet-110和ILSVRC-2012上预训练的ResNet18收集的统计信息验证了之前的分析。小的绿色垂直线表示该正态分布中的每个观测值，蓝色曲线表示核分布估计(KDE)[30]，这是一种估计随机变量概率密度函数的非参数方法。画出了两种结构的第一层和最后一层的范数分布。此外，为了清楚地说明范数点之间的关系，提出了两种不同的x尺度，即线性x尺度和对数x尺度。

        （1） 网络中的小范数偏差。对于ResNet-110的第一卷积层，如图3（b）所示，有大量的滤波器，其范数集中在.对于ResNet-110的最后一个卷积层，如图3（c）所示，范数值的间隔跨度大约为0.3，这比第一层范数的间隔跨度（1.7）小得多。对于ResNet-18的最后一卷积层，正如图3（g）所示的，大多数滤波器范数都在间隔[0.8，1.0]之间。在所有这些情况下，滤波器分布得太密集，这使得难以选择适当的阈值来将重要滤波器与其他滤波器区分开来。

        （2） 网络中的大最小范数。对于ResNet-18的最后一个卷积层，如图3（g）所示，这些滤波器的最小范数约为0.8，与第一个卷积层中的滤波器相比，这是很大的（图3（e））。对于ResNet-110的最后一个卷积层，如图3（c）所示，只有一个滤波器是任意小的，而其他滤波器不是。在这些情况下，尽管根据基于规范的标准，具有最小规范的过滤器相对不那么重要，但仍然在网络中做出了重要贡献。

 图3。CIFAR-10上ResNet-110和ILSVRC-2012上ResNet-18不同层滤波器的标准分布。小的绿色垂直线和蓝色曲线分别表示范数分布的每个范数和核分布估计（KDE）。

3.4 通过几何中值进行过滤修剪

        为了消除基于范数的准则中的约束，我们提出了一种新的基于几何中值的滤波器修剪方法。几何中值[8]的中心思想如下：给定一组n个点，.....，对于每个∈，找到一个点，使到它们的欧几里得距离之和最小化：

         由于几何中值是欧几里得空间中数据中心性的经典稳健估计[8]，我们使用几何中值来获得单个第i层中所有滤波器的公共信息：

在第i层中，如果某些过滤器具有与该层中的几何中值相同或相似的值，即：

 

那么这些滤波器, 可以由同一层中的其他滤波器表示，因此，修剪它们对网络性能几乎没有负面影响。

        由于几何中值在计算几何中是一个非常重要的问题，因此计算-近似几何中值为通过[2]中的方法， 通过[3]中的方法。在我们的情况下，作为最终结果 是一个已知点列表，即层中的候选过滤器，我们可以将上述问题简单化。

        我们假设

从而实现方程4。则上述等式2变为

 

 注意，即使需要修剪滤波器， , 不包括在公式中几何中值的计算公式6中，我们也可以获得相同的结果。在此设置中，我们要查找滤波器

通过上面的等式6和等式8，我们可以得到：

 

 然后我们可以

         对于等式10右侧的第二个分量，当x=, 我们可以得到：

 

 

由于几何中值是欧几里得空间中数据中心性的经典稳健估计[8]，因此选择的滤波器, 左边的共享最常见的信息。这表示滤波器的信息可以由其他代替。微调后，网络可以很容易地恢复其原始性能，因为修剪后的过滤器的信息可以由剩余的过滤器表示。因此，滤波器对神经网络的最终结果的影响可以忽略不计。FPGM总结在算法1中。

 

3.5. 理论和现实加速

3.5.1理论加速

假设输入张量和输出张量的形状。将第i层的过滤器修剪率设置为，则应修剪过滤器。滤波器修剪后，第i层的输入和输出特征图的维数分别变为 和I'\in[N_i \times (1-P_i)] \times H_i \times W_i。

如果将第（i+1）层的修剪率设置为，则只需要原始计算的。最后，将会获得一个紧凑的模型。

3.5.2 实际加速

在上述分析中，仅考虑了用于计算复杂性比较的卷积运算的FLOP，这在先前的工作中是常见的[21，15]。这是因为与卷积运算相比，诸如批处理归一化（BN）和池化等其他运算无关紧要。

然而，非张量层（例如BN和池化层）也需要GPU上的推理时间[25]，并影响真实加速度。此外，理论和实际加速之间的巨大差距也可能受到IO延迟、缓冲区切换和BLAS库效率的限制。我们比较了表5中的理论加速度和实际加速度。

4.实验

我们在两个基准上评估了单分支网络（VGGNet[31]）和多分支网络（ResNet）的FPGM：CIFAR-10[20]和ILSVRC-2012[29]3。CIFAR-10[20]数据集包含10个不同类别的60000张32×32彩色图像，其中包括50000张训练图像和10000张测试图像。ILSVRC2012[29]是一个大型数据集，包含128万张训练图像和1000个类别的50k张验证图像。

 

4.1实验设置

训练设置。在CIFAR-10上，参数设置与[13]相同，训练计划与[40]相同。在ILSVRC-2012实验中，我们使用与[12，13]相同的默认参数设置。ILSVRC-2012的数据论证策略与PyTorch[28]的官方示例相同。我们分析了从头开始和预训练模型之间的差异。为了从头开始修剪模型，我们使用正常的训练计划，而无需额外的微调过程。为了修剪预先训练的模型，我们将学习率降低到原始学习率的十分之一。为了从头开始修剪模型和预训练模型进行公平比较，我们使用相同的训练时期来训练/微调网络。之前的工作[21]可能使用较少的时间段来微调修剪模型，但它收敛得太早，即使使用较多的时间段，其精度也无法提高，如第4.2节所示。

修剪设置。在过滤器修剪步骤中，我们简单地以相同的修剪速率同时修剪所有加权层，这与[15]相同。因此，只需要一个超参数Pi=P来平衡加速度和精度。修剪操作在每个训练阶段的结束。与之前的工作不同[21]，灵敏度分析在FPGM中不是实现良好性能的关键，这将在后面的章节中进行演示。

        除了FPGM唯一标准外，我们还使用了FPGM和先前基于规范的方法[15]的混合物，以表明FPGM可以作为先前方法的补充。仅FPGM的标准表示为“仅FPGM”，将FPGM和基于规范的标准结合起来的标准表示“FPGM混合”。“仅FPGM 40%”表示仅使用FPGM选择该层的40%过滤器，而“FPGM混合40%”表示使用FPGM选定该层的30%过滤器，其余10%过滤器使用基于规范的标准[15]。我们将FPGM与先前的加速算法进行了比较，例如MIL[5]、PFEC[21]、CP[16]、ThiNet[25]、SFP[15]、NISP[39]、重新思考[38]。毫不奇怪，我们的FPGM方法达到了最先进的结果。

 

 

4.2.单分支网络修剪

CIFAR-10上的VGGNet。由于[21]没有公开的训练设置，我们重新实施了修剪程序，并获得了与原始论文类似的结果。修剪预训练和划痕模型的结果分别显示在表3和表4中。毫不奇怪，FPGM在两种设置中都取得了比[21]更好的性能。

4.3.多分支网络修剪

        CIFAR-10上的ResNet。对于CIFAR-10数据集，我们在ResNet-20、32、56和110上测试了FPGM，使用两种不同的修剪率：30%和40%。

        如表1所示，我们的FPGM达到了最先进的性能。例如，MIL[5]在没有微调的情况下使ResNet-32加速了31.2%的加速比，精度下降了1.59%，但我们的FPGM在没有微调情况下实现了53.2%的加速率，精度甚至提高了0.19%。与SFP[15]相比，当修剪ResNet-56的52.6%FLOP时，我们的FPGM只有0.66%的精度下降，这远远小于SFP[15]（1.33%）。对于修剪预训练的ResNet-110，我们的方法实现了更高（52.3%vs.38.6%）的加速比，性能提高了0.16%，而PFEC[21]以更低的加速比损害了性能。这些结果表明，FPGM可以产生具有可比甚至更好性能的更压缩的模型。

        ILSVRC-2012上的ResNet。对于ILSVRC-2012数据集，我们在ResNet-18、34、50和101上测试了FPGM，修剪率分别为30%和40%。与[15]相同，我们不会为了简化而删减投影快捷方式。

        表2显示，FPGM在ILSVRC-2012数据集上再次优于先前的方法。对于ResNet-18，没有微调的纯FPGM实现了与[15]相同的推理速度，但其精度超过了0.68%。仅进行微调的FPGM甚至可以比仅进行微调时的FPGM获得0.60%的改进，因此超过[15]1.28%。对于ResNet-50，微调后的FPGM比CP实现了更高的推理速度[16]，但我们的修剪模型在精度上超过了他们的模型0.85%。此外，对于修剪预训练的ResNet-101，FPGM减少了模型40%以上的FLOP，而没有前5位的精度损失，只有可忽略的（0.05%）前1位精度损失。相比之下，重新思考的性能下降了2.10%[38]。与基于范数的准则相比，几何中值（GM）明确地利用了滤波器之间的关系，这是其优越性能的主要原因

        为了比较理论和实际加速度，我们在一个GTX1080 GPU上测量了批处理大小为64的修剪模型的前进时间。结果4如表5所示。如上一节所述，理论模型和现实模型之间的差距可能来自于IO延迟、缓冲区切换和BLAS库效率的限制。

4.4.消融研究

         修剪间隔的影响在我们的实验设置中，修剪间隔等于1，即，我们在每个训练阶段结束时进行修剪操作。为了探讨修剪间隔的影响，我们将修剪间隔从一个时期更改为十个时期。我们使用修剪率为40%的ResNet-110作为基线，如图4（a）所示。不同修剪间隔的精度波动小于0.3%，这意味着修剪性能对该参数不敏感。请注意，微调此参数甚至可以获得更好的性能。

         改变修剪的FLOP我们改变ResNet-110的修剪FLOP的比率，以全面了解FPGM，如图4（b）所示。当修剪的FLOP为18%和40%时，修剪模型的性能甚至超过了没有修剪的基线模型，这表明FPGM可能对神经网络具有正则化效果。

        距离类型的影响我们使用“1-范数和余弦距离”代替方程3中的距离函数。我们使用修剪率为40%的ResNet-110作为基线，修剪模型的准确度为93.73±0.23%。基于“1范数”和“余弦距离”的精度分别为93.87±0.22%和93.56±0.13。使用“1-范数”作为滤波器的距离会带来稍好的结果，但余弦距离作为距离会稍微损害网络的性能。

        将FPGM与基于规范的准则相结合我们分析了FPGM与先前基于规范的标准相结合的效果。对于CIFAR-10上的ResNet-110，FPGMmix仅略优于FPGM。对于ILSVRC-2012上的ResNet-18，仅FPGM和混合FPGM的性能几乎相同。看来，标准化标准和FPGM一起可以提高CIFAR-10的性能，但不能提高ILSVRC-2012的性能。我们认为，这是因为基于规范的标准的两个要求在CIFAR-10预训练网络的某些层上得到满足，但在ILSVRC-2012预训练网络上没有得到满足，如图3所示。

4.5.特征图可视化

我们可视化ResNet-50的第一块的第一层的特征图。当将修剪率设置为10%时，带有红色标题的特征图（7、23、27、46、56、58）对应于选定的过滤器激活。这些选定的特征图包含竹子和熊猫头部和身体的轮廓，可由其他特征图代替：（5,12,16,18,22等）包含竹子的轮廓，（0,4,33,34,47等）包含熊猫的轮廓。

 

 

5.结论和未来工作

在本文中，我们阐述了基于范数的滤波器修剪准则的基本要求，并指出了它们的局限性。为了解决这个问题，我们提出了一种新的基于几何中值的滤波器修剪策略，称为FPGM，以加速深度神经网络。与之前的标准不同，FPGM明确考虑了过滤器之间的相互关系。得益于此，FPGM在多个基准测试中取得了最先进的性能。未来，我们计划研究如何将FPGM与其他加速算法（例如矩阵分解和低精度权重）相结合，以将性能推向更高的阶段。