【深度学习】模型选择、欠/过拟合和感受野(三)
文章目录
-
- 模型选择
-
- 泛化能力
- 过拟合和欠拟合
- 模型复杂度
- 感受野
-
- 感受野如何计算?
- 总结
写在最前面的话:这一篇文章要整理的知识点有点稀疏,内容不是很多。
模型选择
在深度学习中,不同的参数设置,不同的隐层数量对模型都有相应的影响,但是经过训练后,它们最终都可以达到相同的实验结果,那么我们该如何对这些模型作选择呢,对不同的条件下的模型选出一个相对较好的模型?其实,模型的选择方式可以通过超参数的设置,模型的容量、验证集的情况来定。
泛化能力
在【深度学习】理解栏目(二)中,我们提到了泛化能力这个概念。泛化能力 是指模型对未知数据的预测能力,是一种用于评估机器学习算法的能力的指标。而泛化误差可以反映模型的泛化能力,误差越小,模型越稳定。泛化误差(generalization error) 又是指训练后的模型在测试集上的误差,也叫测试误差(test error)。通常情况下,我们都是利用最小化训练误差来训练模型,但是我们并不关心训练模型的误差结果,而是关心测试误差,因为测试误差是模型在测试集上的平均损失,反映了模型对未知测试数据集的预测能力。
验证数据集跟测试集作用差不多,验证集也是未经模型训练过的数据集,但从严格意义上说,测试集只能在模型训练完毕,所有参数都被选定后才能使用的,我们不能在训练过程中使用测试集来选择参数,更不能从训练误差中估计出泛化误差。因此,我们可通过预留一小部分数据,作为训练时用于辅助模型在训练过程中对参数的选择,这部分数据即为验证集。
过拟合和欠拟合
决定机器学习算法效果的两个重要因素是:降低训练误差、缩小训练误差和测试误差的差距。而这两个因素主要受到模型复杂度和训练数据集的大小的影响,因而产生两个典型问题:过拟合和欠拟合。

过拟合(overfitting): 选择的模型中包含了过多的参数,以至于模型对已知数据(训练集)预测得非常好,但是对于未知的数据(测试集)预测结果很差,使得模型的训练误差远小于它在测试数据集上的误差,这种现象称为过拟合。产生的原因是训练样本中有些标注错误的样本或者样本本身的特点被当作潜在样本都具有的一般性质,因而造成泛化能力下降。过拟合不能避免,只能通过减少训练集的大小,或者采用正则化,又或者使用dropout(在随机层去掉一部分神经元)来缓解。
欠拟合(underfitting):选择的模型包含参数太少,以至于模型对已知数据(训练集)的预测都很差,使得训练误差较大,就更不用说测试集的情况了。产生的原因是学习能力低下。可采用增加训练数据,优化算法来解决。
模型复杂度
模型复杂度,直观地拿多项式函数来说,是高阶和低阶的区别,高阶多项式参数多,而低阶多项式参数少,因此高阶比低阶复杂度高。模型的复杂度也反映模型的容量大小。容量小的模型容易出现欠拟合,模型拟合能力过弱;容量大的模型容易出现过拟合,模型拟合能力过强。我们可以通过选择不同的假设空间来改变模型的容量。
假设空间:是指所有可能的函数/模型组成的一个空间,它代指模型的函数集合,即模型的表示容量(representational capacity),但由于某些限制(比如优化算法不完善,损失函数不好等),无法使得所有可能的函数都实现,只能有其中一部分函数成功,称为模型的有效容量(effective capacity)。模型的有效容量一般小于模型的表示容量。
如何在模型的假设空间中选出最佳函数呢?对于实际操作起来,这是一个非常困难的优化问题,鉴于局限,在实际应用中我们只能选取一个训练误差足够低的函数作为最佳函数。
感受野
最后,我突然想起感受野这个概念,因此想着顺便梳理一下(专业术语插得有点突然…)。感受野的解释是 在神经网络中,用来表示网络内部的不同位置的神经元对输入图像的感受范围的大小。(我还是不太懂,“感受”这词有点抽象)再具体一点,就是神经网络的每一层的输出(叫特征图)上的每一个像素点对应输入图上的区域大小。如下图所示:
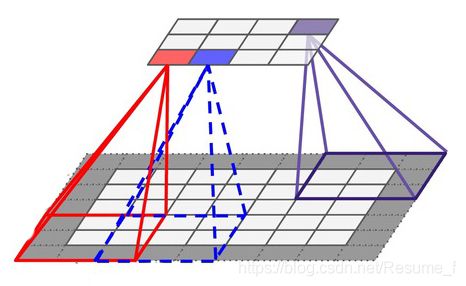
有图就很好理解了。上图中,有上下两个矩形:上为小矩形,假设是当前层输出的特征图,一共12个浅灰色小格;下为大矩形,假设为当前层为输入的图像,一共28个浅灰色小格,(深灰格是池化后的结果),那么输出的特征图中,红色这一个像素格对应的是下面红框的区域为它的感受野。
感受野如何计算?
了解了什么是感受野之后,该如何计算感受野呢?下面要举栗子啦~~

原图(Raw Image)是一个7x7大小的矩形,初始输入图像的每个单元的感受野被定义为1。第一层卷积(conv1)输出的是3x3大小的特征图,每个单元的感受野的大小为3,第二层卷积(conv2)输出的是2x2大小的特征图,每个单元的感受野为5。
计算方式如下,为了方便解释,我们需要定义一些符号,用 r n r_n rn表示第n格卷积层中,每个单元的感受野的大小; k n k_n kn和 s n s_n sn分别表示第n格卷积层的kernel size核大小和stride步长。对Raw Image进行kernel_size=3, stride=2,padding=0的卷积操作得到conv1的输出,那么根据卷积输出公式:
F e a t u r e s i z e = ( I n p u t s i z e − k e r n e l s i z e + 2 ∗ p a d d i n g ) s t r i d e + 1 Feature_{size}=\frac{(Input_{size}-kernel_{size}+2*padding)}{stride}+1 Featuresize=stride(Inputsize−kernelsize+2∗padding)+1
得到输出特征图的大小为(7-3)/2+1=3,根据感受野大小的公式(来自知乎上一个大佬的总结):
r n = r n − 1 + ( k n − 1 ) ∏ i = 1 n − 1 s i r_n=r_{n-1}+(k_n-1)\prod_{i=1}^{n-1}s_i rn=rn−1+(kn−1)i=1∏n−1si
其中 r 0 = 1 r_0=1 r0=1,得到conv1的每个单元的感受野为(1+(3-1)x1)=3,conv2的每个单元的感受野为(3+(2-1)x2)=5。
感受野的中心公式:
c e n t e r n = c e n t e r n − 1 + ( k n − 1 2 − p a d d i n g n ) ∗ s n − 1 center_n=center_{n-1}+(\frac{k_n-1}{2}-padding_n)*s_{n-1} centern=centern−1+(2kn−1−paddingn)∗sn−1
那么,知道感受野有什么作用呢?别人说,理解感受野有两个好处,一,理解卷积的本质;二,更好的理解CNN的整个架构。我认为,理解感受野能帮助设计网络结构,可以大概知道每一层网络覆盖原图的哪一部分,获取了什么特征的信息,如果该层的感受野的值很大,那么表示它包含的原图范围很大,获取的特征可能是高层次特征,相反,感受野很小,则包含的特征趋向于局部细节,更是低层次的特征。因此,知道感受野,可以用来大致判断神经网络中每一层的抽象意义。
总结
本文主要介绍了模型选择、欠拟合、过拟合以及感受野的相关概念和计算,又进一步了解地扫盲深度学习的知识点~哈哈,今天的笔记特别简单,理解也很轻松!还是那句话,如有错误,欢迎指出,谢谢支持!
参考文章:
http://www.huaxiaozhuan.com/%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0/chapters/9_model_selection.html
https://zhuanlan.zhihu.com/p/28492837
https://www.cnblogs.com/augustone/p/10528148.html
添加链接描述