泊松融合原理浅析

前言

图像融合是图像处理领域的一个子领域，主要目的是将不同图像的一部分放在一起，融合得到一张新的图像。结果越自然，说明该融合算法就越好。常见的融合算法有Alpha blending、Laplacian Pyramid blending（拉普拉斯金字塔融合/多频带融合）和Poisson Blending。

泊松融合（Poisson Blending）是图像处理领域著名的图像融合算法，自从2003年发表以来，有很多基于此算法的应用和改进研究出现。泊松融合无需像Alpha blending一样的精确抠图就可以得到很自然的结果。

数学知识预备

梯度，拉普拉斯，散度：

拉普拉斯方程，又名调和方程、位势方程，是一种偏微分方程。因为由法国数学家皮埃尔-西蒙·拉普拉斯首先提出而得名。求解拉普拉斯方程是电磁学、天文学、热力学和流体力学等领域经常遇到的一类重要的数学问题，因为这种方程以势函数的形式描写电场、引力场和流场等物理对象（一般统称为“保守场”或“有势场”）的性质。

二维拉普拉斯方程如下：



拉普拉斯方程是泊松方程的一个特例。

论文内容解析

泊松融合的核心思想不是让需要融合的两张图像直接叠加，而是让目标图像（dst）在融合部分根据源图像（src）的引导场（实际是梯度场 gradient field ）“生长”出新的图像。

也就是说，只需要提供源图像的梯度场，让目标图像根据自身特点，按照源图像对应的梯度场生成融合部分。由于目标图像是按照自身特点出发生成融合区域，所以融合结果会显得更加自然。

在论文中，作者将这种梯度场引导插值操作统一称为“泊松编辑（Poisson Image Editing）”。根据梯度场的处理不同，泊松融合可以分为NORMAL CLONE、MIXED CLONE、MONOCHROME TRANSFER三大类。泊松编辑除了泊松融合外还有Texture flattening、Local illumination changes、Local color changes等应用场景。

在示意图图一中，$S$是二维实数集${\mathbb{R}}^2$的闭合子集，$\Omega$是$S$的边界为$\partial \Omega$闭合子集。$f^{\ast }$是集合 $S-\Omega$ 部分的函数（如果是图像的话就是指所有像素的像素值），$f$是集合 $\Omega$ 的函数（也就是需要靠解泊松方程来求的函数）。$\mathbf{v}$是集合$\Omega$的向量场（构建泊松方程所需）。

最简单的插值结果是如下最小化问题的解：


该问题的解必须满足其Euler-Lagrange等式：


等式(2)是带有狄利克雷边界条件的拉普拉斯方程。

在图像融合中，这种简单的插值方法会产生不连续、模糊的插值效果。这时候可以通过引入集合$\Omega$的向量场$\mathbf{v}$来改善。以此方式构建的最小化问题如下：

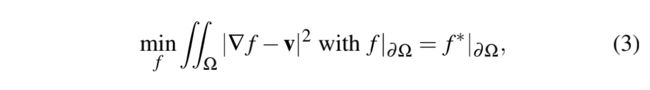
该问题的解是如下带有狄利克雷边界条件的泊松方程。


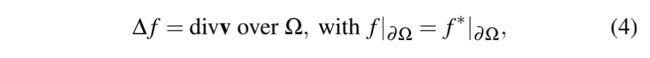
也就是说，拉普拉斯方程是泊松方程的一种特例（divv=0）。

需要注意的是上述过程的求解是针对图像单个通道的，如果是RGB通道则需要构建三个泊松方程求解。

对于图像而言，像素点是离散点，因此上述连续空间的偏微分方程可以改写为离散空间的偏微分方程：

其中，p是S中的像素点，$N_p$是像素p的四邻域，是像素对。此时$\Omega$的边界变为$\partial \Omega =\{p\in S\setminus \Omega :N_p\cap \Omega \ne \varnothing \}$。$f_p$是$f$在p点的值。

等式(6)的解满足如下联立线性方程：

当方程中的像素p的四邻域不包含边界点（$\partial \Omega$）时：

关于泊松方程的求解，原论文中有如下描述：

方程(7)形式构成一个经典的、稀疏带状、对称、正定系统。可以通过带successive overrelaxation（逐次超松弛）的Gauss-Seidel iteration（高斯-赛德尔迭代）或者V-cycle multigrid方法求解。

根据泊松方程构建形式的不同可以选择上述两种不同的方法进行求解。

另外梯度场V不仅可以是源图像的梯度场，还可以是其他。对引导场进行设计可以将泊松编辑应用到各种场景中：

NORMAL CLONE

MIXED CLONE

MONOCHROME TRANSFER
Texture flattening

Local illumination changes

Local color changes

方法原理

泊松融合的目的是将源图像的一部分无缝融合到目标图像上。其本质是在保持目标图在融合边界的像素的同时以源图像的该部分的梯度场作为指导来生成融合区域内的像素。整体原则是保持融合区域内的生成像素的梯度场与源图像融合部分的像素的梯度场尽可能一致，反映到方程求解中则是梯度差异尽可能小。也就是让生成区域的拉普拉斯结果和源图像的拉普拉斯结果一致，且生成区域边界的的值和目标图像在融合区域的边界值一致。

以一维场景为例说明，如下图，需要将左侧直方图中红色的部分融合到右侧直方图中的空缺处，红色柱子上方的数值是其梯度。

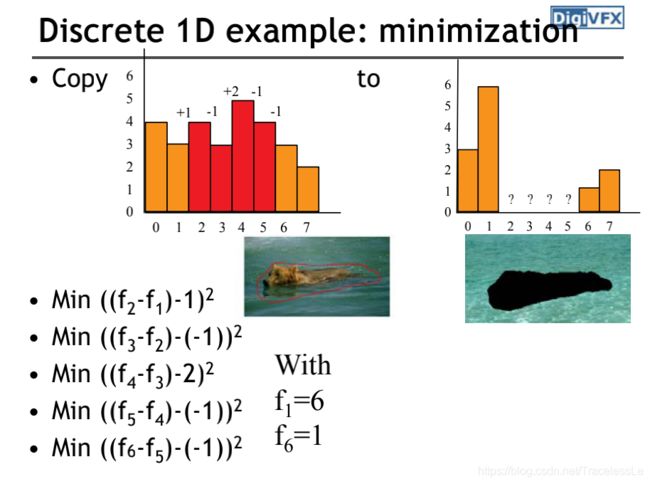
根据方程：

可以列出：

将$f_1$和$f_6$的值代入并展开：

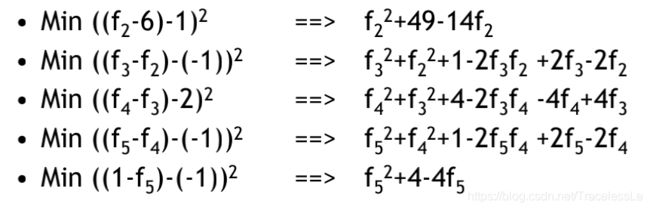
对所有min(*)进行求和：

求偏导：

写成矩阵形式：

矩阵求解：

融合结果如下：

对于二维图像而言：

X方向和Y方向的梯度可以求得：

可以通过得到的梯度场和边界像素重建回原始图像：

将图像G融合到图像I上：

改写成矩阵形式：



对于$N\ast N$大小的图像，矩阵A的大小$N^2\ast N^2$，存储A是不现实的，由于A在形式上是稀疏、对称、正定的，可以选用如下方法进行求解：

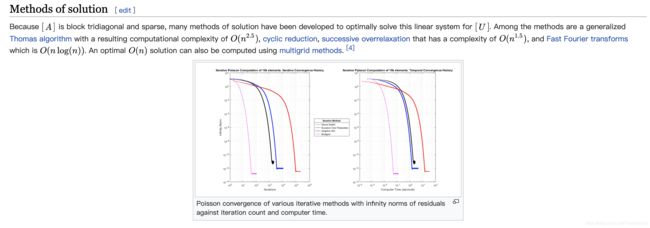
维基百科中列出的解法：

OpenCV实现

OpenCV已经有泊松融合（编辑）的实现代码，接口如下：

最基本的泊松融合函数如下：

OpenCV GitHub源码：

关于泊松融合OpenCV实现代码将在后续博客中进行详解，值得一提的是OpenCV中的泊松方程求解采用了离散傅里叶变换方法，有兴趣可以详读该部分源码。

代码示例

import cv2

src_bgr = cv2.imread('xingye.jpg', 1)
dst_bgr = cv2.imread('xiangrikui.jpg', 1)

resize = (70, 120)
src_bgr_resize = cv2.resize(src_bgr, (resize[1], resize[0]))
mask = np.ones((src_bgr_resize.shape[0], src_bgr_resize.shape[1]))

mask_inner = mask[1:-1, 1:-1]
mask = cv2.copyMakeBorder(mask_inner, 1, 1, 1, 1, cv2.BORDER_ISOLATED | cv2.BORDER_CONSTANT, value=0)

mask = mask*255

p = (290, 610)

out_img = cv2.seamlessClone(src_bgr_resize.astype(np.uint8), dst_bgr.astype(np.uint8), mask.astype(np.uint8), p, cv2.NORMAL_CLONE)

cv2.imwrite('out_img.png', out_img)

xingye.jpg:

xiangrikui.jpg:

out_img.png:

参考资料

[1] OpenCV Docs - Seamless Cloning
[2] OpenCV GitHub - opencv/modules/photo/src/seamless_cloning.cpp
[3] OpenCV GitHub - opencv/modules/photo/src/seamless_cloning_impl.cpp
[4] csdn - 图像处理（十二）图像融合(1)Seamless cloning泊松克隆-Siggraph 2004
[5] 知乎 - 12. 泊松图像编辑
[6] 图像融合之泊松融合（Possion Matting） - 一度逍遥 - 博客园
[7] 盲解卷积和泊松图像融合 - 哔哩哔哩
[8] OpenCV Docs - Image Filtering
[9] OpenCV Docs - cv::dft
[10] OpenCV Docs - cv::cuda::createLaplacianFilter
[11] OpenCV Docs - cv::cuda::DFT
[12] OpenCV GitHub - opencv_contrib/modules/cudaarithm/src/arithm.cpp
[13] Poisson equation, solving with DFT - Algowiki
[14] Numerical Analysis of Boundary-Value Problems (AMATH 585)
[15] 矩阵计算
[16] Opencv中使用cuda进行 dft 与 idft滤波运算 | YangYouji’s WebSite
[17] OpenCV Docs - cv::filter2D
[18] OpenCV Docs - Discrete Fourier Transform
[19] 快速傅里叶变换 - 维基百科，自由的百科全书
[20] opencv之Mat数据类型 - feifanren - 博客园
[21] python - OpenCV cv2.seamlessClone中的错误 - 堆栈内存溢出
[22] python - bug on bounds in OpenCV cv2.seamlessClone - Stack Overflow
[23] seamlessClone bug · Issue #15294 · opencv/opencv
[24] epock / epock / issues / #48 - terminate called after throwing an instance of ‘std::length_error’ — Bitbucket
[25] opencv/pyopencv_cuda.hpp at master · opencv/opencv
[26] 计算机视觉：泊松融合
[27] 松弛法求解给定边界条件的泊松方程
[28] 泊松融合笔记
[29] FFT解泊松方程
[30] 拉普拉斯方程 - 维基百科，自由的百科全书
[31] 泊松方程 - 维基百科，自由的百科全书
[32] Discrete Poisson equation - Wikipedia
[33] OpenCV: samples/cpp/tutorial_code/photo/seamless_cloning/cloning_demo.cpp
[34] 图像融合之多波段融合（Multiband Blending）/拉普拉斯金字塔融合（Laplacian Pyramid Blending）
[35] An Intuitive Explanation of using Poisson Blending for Seamless Copy-and-Paste of Images