基于误差反传的多层感知器——BP神经网络
郑重声明:以下内容,完全参考韩力群编著的《人工神经网络理论,设计及应用》
BP算法的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。
1. BP网络模型
我们以单隐层感知器为例进行BP网络模型的说明,一般习惯将单隐层感知器称为三层感知器,所谓三层包括了输入层,隐层和输出层。
三层感知器中,输入向量为 X = ( x 1 , x 2 , ⋯ , x i , ⋯ , x n ) T \bm X=(x_1,x_2,\cdots,x_i,\cdots,x_n)^T X=(x1,x2,⋯,xi,⋯,xn)T,图中 x 0 = − 1 x_0=-1 x0=−1是为隐层神经元引入阈值而设置的;隐层输出向量为 Y = ( y 1 , y 2 , ⋯ , y j , ⋯ , y m ) T \bm Y=(y_1,y_2,\cdots,y_j,\cdots,y_m)^T Y=(y1,y2,⋯,yj,⋯,ym)T,图中 y 0 = − 1 y_0=-1 y0=−1是为输出层神经元引入阈值而设置的;输出层的向量为 O = ( o 1 , o 2 , ⋯ , o k , ⋯ , o l ) T \bm O=(o_1,o_2,\cdots,o_k,\cdots,o_l)^T O=(o1,o2,⋯,ok,⋯,ol)T;期望输出向量为 d = ( d 1 , d 2 , ⋯ , d k , ⋯ , d l ) T \bm d=(d_1,d_2,\cdots,d_k,\cdots,d_l)^T d=(d1,d2,⋯,dk,⋯,dl)T。
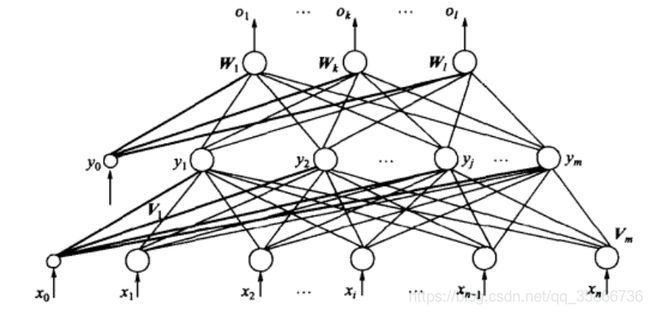
输入层到隐层之间的权值矩阵用 V \bm V V表示, V = ( V 1 , V 2 , ⋯ , V j , ⋯ , V m ) \bm V=(\bm V_1,\bm V_2,\cdots,\bm V_j,\cdots,\bm V_m) V=(V1,V2,⋯,Vj,⋯,Vm),其中列向量 V j \bm V_j Vj为隐层第 j j j个神经元对应的权向量,隐层到输出层之间的权值矩阵用 W \bm W W表示, W = ( W 1 , W 2 , ⋯ , W k , ⋯ , W l ) \bm W=(\bm W_1,\bm W_2,\cdots,\bm W_k,\cdots,\bm W_l) W=(W1,W2,⋯,Wk,⋯,Wl),其中列向量 W k \bm W_k Wk为输出层第 k k k个神经元对应的权向量。
下面分析各层信号之间的数学关系。
对于输出层,有:
o k = f ( n e t k ) k = 1 , 2 , ⋯ , l (1.1) o_k=f({\rm net}_k)\quad\quad k=1,2,\cdots,l \tag{1.1} ok=f(netk)k=1,2,⋯,l(1.1) n e t k = ∑ j = 0 m w j k y j k = 1 , 2 , ⋯ , l (1.2) {\rm net}_k=\sum^m_{j=0}w_{jk}y_j\quad k=1,2,\cdots,l \tag{1.2} netk=j=0∑mwjkyjk=1,2,⋯,l(1.2)对于隐层,有:
y i = f ( n e t j ) j = 1 , 2 , ⋯ , m (1.3) y_i=f({\rm net}_j)\quad\quad j=1,2,\cdots,m\tag{1.3} yi=f(netj)j=1,2,⋯,m(1.3) n e t j = ∑ i = 0 n v i j x i j = 1 , 2 , ⋯ , m (1.4) {\rm net}_j=\sum^n_{i=0}v_{ij}x_i\quad j=1,2,\cdots,m\tag{1.4} netj=i=0∑nvijxij=1,2,⋯,m(1.4)以上两式中,激活函数(转移函数) f ( x ) f(x) f(x)均为单极性Sigmoid函数:
f ( x ) = 1 1 + e − x (1.5) f(x)=\frac{1}{1+{\rm e}^{-x}}\tag{1.5} f(x)=1+e−x1(1.5) f ( x ) f(x) f(x)具有连续、可导的特点,且有:
f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) (1.6) f'(x)=f(x)(1-f(x))\tag{1.6} f′(x)=f(x)(1−f(x))(1.6) 根据需要,也可以采用双极性Sigmoid函数(或称双曲线正切函数):
f ( x ) = 1 − e − x 1 + e − x (1.7) f(x)=\frac{1-{\rm e}^{-x}}{1+{\rm e}^{-x}}\tag{1.7} f(x)=1+e−x1−e−x(1.7)式(1.1) ~ (1.5)共同构成了三层感知器的数学模型。
2. BP学习算法
下面一三层感知器为例介绍BP学习算法,然后将所得结论推广到一般多层感知器的情况。
2.1 网络误差定义和权值调整思路
在进行下面推导的过程中,我们必须要重视以下符号的含义:
- w j k h w_{jk}^h wjkh:表示第 h − 1 h-1 h−1隐层第 j j j个神经元的输出值 传递到第 h h h隐层第 k k k个神经元时的缩放比例,称之为权值。
- y j h y^h_j yjh:表示第 h h h隐层第 j j j个神经元的输出值,也是 h + 1 h+1 h+1层神经元d 输入值经过权重 w j k h + 1 w_{jk}^{h+1} wjkh+1缩放后的一部分。
- n e t j h {\rm net}_j^h netjh:表示第 h h h隐层第 j j j个神经元的集结输入值, n e t j h = ∑ j = 0 m w i j h y i h − 1 {\rm net}_j^h=\sum^m_{j=0}w^h_{ij}y^{h-1}_i netjh=∑j=0mwijhyih−1。
- f ( n e t j h ) f({\rm net}_j^h) f(netjh):表示第 h h h隐层第 j j j个神经元的激活函数(转移函数),即: y j h = f ( n e t j h ) y_j^h=f({\rm net}_j^h) yjh=f(netjh)
- δ j h \delta^h_j δjh:表示第 h h h隐层第 j j j个神经元的输出误差信号,也称为学习信号,这是因为网络误差函数 E E E 对第 h h h隐层第 j j j个神经元的 n e t j h {\rm net}_j^h netjh求偏导、并取反,即: δ j h = − ∂ E n e t j h = − ∂ E ∂ y j h ∂ y j h ∂ n e t j h = − ∂ E ∂ y j h f ′ ( n e t j h ) \delta^h_j=-\frac{\partial E}{{\rm net}_j^h}=-\frac{\partial E}{\partial y^h_j}\frac{\partial y^h_j}{\partial {\rm net}^h_j}=-\frac{\partial E}{\partial y^h_j}f'({\rm net}^h_j) δjh=−netjh∂E=−∂yjh∂E∂netjh∂yjh=−∂yjh∂Ef′(netjh)
- Δ w i j h \Delta w^h_{ij} Δwijh:表示经过一些列计算,确定当前第 h − 1 h-1 h−1隐层第 i i i个神经元到第 h h h隐层第 j j j个神经元的权值要调整的具体数值 Δ w i j h = η δ j h y i h − 1 \Delta w^h_{ij}=\eta\delta^h_jy^{h-1}_i Δwijh=ηδjhyih−1
- 理解BP算法的核心是要懂得,所有的推导铺垫都是在为某一隐层或输出层的权值函数 v i j v_{ij} vij或 w j k w_{jk} wjk做铺垫的。
- 如果把某一隐层或输出层的权值数看作是矩阵,则应该是这样的: V ( n + 1 ) × m = ( V 1 , V 2 , ⋯ , V m ) = ( v 11 v 12 ⋯ v 1 m v 21 v 22 ⋯ v 2 m ⋮ ⋱ ⋮ v ( n + 1 ) 1 v ( n + 1 ) 2 ⋯ v ( n + 1 ) m ) V^{(n+1)\times m}=(V_1,V_2,\cdots,V_m)=\begin{pmatrix}v_{11}&v_{12}&\cdots&v_{1m}\\ v_{21}&v_{22}&\cdots&v_{2m}\\ \vdots& &\ddots&\vdots\\ v_{(n+1)1}&v_{(n+1)2}&\cdots&v_{(n+1)m} \end{pmatrix} V(n+1)×m=(V1,V2,⋯,Vm)=⎝⎜⎜⎜⎛v11v21⋮v(n+1)1v12v22v(n+1)2⋯⋯⋱⋯v1mv2m⋮v(n+1)m⎠⎟⎟⎟⎞
理解这个矩阵构造的关键在于理解:- 列数代表当前隐藏层的神经元个数,当前矩阵显示本隐藏层有 m m m个神经元;
- 当前隐藏层的权值矩阵的每一列代表相应的一个神经元所对应于上一层隐藏层(或输入层)神经元的一系列权值,例如上式中 V 1 V_1 V1表示该隐藏层第一个神经元对应于上一隐藏层各神经元的权值,假设上一层有 n n n个神经元,由于还要考虑将阈值引入到当前隐藏层中,故上一层隐藏层还要加一个输出值固定为"-1"的神经元,因此上一层共有 n + 1 n+1 n+1个神经元,因此 V 1 = ( v 11 , v 21 , v 31 , ⋯ , v ( n + 1 ) 1 ) T V_1=(v_{11},v_{21},v_{31},\cdots,v_{(n+1)1})^T V1=(v11,v21,v31,⋯,v(n+1)1)T
——————————————————————————————————————————
- 还要理解好学习信号 δ j h \delta^h_{j} δjh,他表示第 h h h个隐藏层中第 j j j个神经元的学习信号,注意, δ j h \delta^h_{j} δjh是标量,但他将负责参与求出权值 V j V_j Vj列向量的一系列列权值,因为 δ j h = − ∂ E ∂ n e t j h = − ∂ E ∂ y j h f ′ ( n e t j h ) \delta^h_{j}=-\frac{\partial E}{\partial net^h_j}=-\frac{\partial E}{\partial y^h_j}f'(net^h_j) δjh=−∂netjh∂E=−∂yjh∂Ef′(netjh) y j h = f ( n e t j h ) = f ( ∑ i = 0 n y h − 1 v i j ) y^h_j=f(net^h_j)=f\left(\sum^n_{i=0}y^{h-1}v_{ij}\right) yjh=f(netjh)=f(i=0∑nyh−1vij) 所以权值 Δ V j h = Δ v i j h = η δ j h y i h − 1 i = 0 , 1 , 2 , ⋯ , n \Delta V_j^h=\Delta v^h_{ij}=\eta\delta^h_jy^{h-1}_i\quad i=0,1,2,\cdots,n ΔVjh=Δvijh=ηδjhyih−1i=0,1,2,⋯,n
- 对于同一条训练数据而言,不同的神经元有不同的 δ j h \delta^h_j δjh;对于同一层的同一位置的神经元,不同的训练数据有不同的 δ j h \delta^h_j δjh。
以上说明中多写了一部分结论,具体推导请看下文。
-
网络误差定义
当网络输出与期望输出不等时,存在输出误差 E E E,定义如下:
E = 1 2 ∣ ∣ d − O ∣ ∣ 2 2 = 1 2 ∑ k = 1 l ( d k − o k ) 2 (2.1) E=\frac{1}{2}||\bm d-\bm O||_2^2=\frac{1}{2}\sum^l_{k=1}(d_k-o_k)^2\tag{2.1} E=21∣∣d−O∣∣22=21k=1∑l(dk−ok)2(2.1)将以上误差定义是展开至隐层,有:
E = 1 2 ∑ k = 1 l [ d k − f ( n e t k ) ] 2 = 1 2 ∑ k = 1 l [ d k − f ( ∑ j = 0 m w j k y j ) ] 2 (2.2) \begin{aligned}E&=\frac{1}{2}\sum^l_{k=1}[d_k-f({\rm net}_k)]^2\\ &=\frac{1}{2}\sum^l_{k=1}[d_k-f(\sum^m_{j=0}w_{jk}y_j)]^2 \tag{2.2}\end{aligned} E=21k=1∑l[dk−f(netk)]2=21k=1∑l[dk−f(j=0∑mwjkyj)]2(2.2) 进一步展开至输入层,有:
E = 1 2 ∑ k = 1 l { d k − f [ ∑ j = 0 m w j k f ( n e t j ) ] } 2 = 1 2 ∑ k = 1 l { d k − f [ ∑ j = 0 m w j k f ( ∑ i = 0 n v i j x i ) ] } 2 (2.3) \begin{aligned}E&=\frac{1}{2}\sum^l_{k=1}\{d_k-f[\sum^m_{j=0}w_{jk}f({\rm net}_j)]\}^2\\ &=\frac{1}{2}\sum^l_{k=1}\{d_k-f[\sum^m_{j=0}w_{jk}f(\sum^n_{i=0}v_{ij}x_i)]\}^2 \tag{2.3}\end{aligned} E=21k=1∑l{dk−f[j=0∑mwjkf(netj)]}2=21k=1∑l{dk−f[j=0∑mwjkf(i=0∑nvijxi)]}2(2.3) -
权值调整思路
从上式可以看出,网络误差是关于各层权值 w j k 、 v i j w_{jk}、v_{ij} wjk、vij的函数,因此调整权值可以改变误差 E E E。
调整权值的原则是使误差不断地减小,因此,应使权值的调整量与误差的梯度下降成正比,即:
Δ w j k = − η ∂ E ∂ w j k j = 0 , 1 , 2 , ⋯ , m ; k = 1 , 2 , ⋯ , l (2.4a) \Delta w_{jk}=-\eta\frac{\partial E}{\partial w_{jk}}\quad\quad j=0,1,2,\cdots,m;\quad k=1,2,\cdots,l\tag{2.4a} Δwjk=−η∂wjk∂Ej=0,1,2,⋯,m;k=1,2,⋯,l(2.4a) Δ v i j = − η ∂ E ∂ v i j i = 0 , 1 , 2 , ⋯ , n ; j = 1 , 2 , ⋯ , m (2.4b) \Delta v_{ij}=-\eta\frac{\partial E}{\partial v_{ij}}\quad\quad i=0,1,2,\cdots,n;\quad j=1,2,\cdots,m\tag{2.4b} Δvij=−η∂vij∂Ei=0,1,2,⋯,n;j=1,2,⋯,m(2.4b) 式中,符号表示梯度下降,常数 η ∈ ( 0 , 1 ) \eta\in(0,1) η∈(0,1)表示比例系数,在训练中反映学习速率。
2.2 BP算法的推导
式 ( 2.4 ) (2.4) (2.4)仅是对权值调整思路的数学表达式,而不是具体的权值调整计算式。下面推导三层BP算法权值调整的计算式。事先约定,在全部推导过程中,对输出层均有 j = 0 , 1 , 2 , ⋯ , m j=0,1,2,\cdots,m j=0,1,2,⋯,m, k = 1 , 2 , ⋯ , l k=1,2,\cdots,l k=1,2,⋯,l;对隐层均有 i = 0 , 1 , 2 , ⋯ , n i=0,1,2,\cdots,n i=0,1,2,⋯,n, j = 1 , 2 , ⋯ , m j=1,2,\cdots,m j=1,2,⋯,m。这是因为如果把当前隐层当成是相对于下一层的输入层,则必须要夹带 y 0 = − 1 y_0=-1 y0=−1的一个当前层神经元作为引入下一层的阈值的设置;而如果仅仅是求取当前隐层的输出值,则无须考虑“为下一隐层引入阈值而设置的当前隐层中的 y 0 = − 1 y_0=-1 y0=−1”,因为作为下一层的输入值,他永远是等于“-1”。
对于输出层,式 ( 2.4 a ) (2.4a) (2.4a)可写为: Δ w j k = − η ∂ E ∂ w j k = − η ∂ E ∂ n e t k ∂ n e t k ∂ w j k (2.5a) \Delta w_{jk}=-\eta\frac{\partial E}{\partial w_{jk}}=-\eta\frac{\partial E}{\partial {\rm net}_k}\frac{\partial {\rm net}_k}{\partial w_{jk}}\tag{2.5a} Δwjk=−η∂wjk∂E=−η∂netk∂E∂wjk∂netk(2.5a) 对于隐层,式 ( 2.4 b ) (2.4b) (2.4b)可写为:
Δ v i j = − η ∂ E ∂ v i j = − η ∂ E ∂ n e t j ∂ n e t j ∂ v i j (2.5b) \Delta v_{ij}=-\eta\frac{\partial E}{\partial v_{ij}}=-\eta\frac{\partial E}{\partial {\rm net}_j}\frac{\partial {\rm net}_j}{\partial v_{ij}}\tag{2.5b} Δvij=−η∂vij∂E=−η∂netj∂E∂vij∂netj(2.5b)
对于输出层和隐层各定义一个误差信号,令: δ k o = − ∂ E ∂ n e t k (2.6a) \delta^o_k=-\frac{\partial E}{\partial {\rm net}_k}\tag{2.6a} δko=−∂netk∂E(2.6a) δ j y = − ∂ E ∂ n e t j (2.6b) \delta^y_j=-\frac{\partial E}{\partial {\rm net}_j}\tag{2.6b} δjy=−∂netj∂E(2.6b) 综合应用式 ( 1.2 ) (1.2) (1.2)和式 ( 2.6 a ) (2.6a) (2.6a),可将式 ( 2.5 a ) (2.5a) (2.5a)的权值调整式改写为:
Δ w j k = η δ k o y j (2.7a) \Delta w_{jk}=\eta\delta^o_ky_j\tag{2.7a} Δwjk=ηδkoyj(2.7a) Δ v i j = η δ j y x i (2.7b) \Delta v_{ij}=\eta\delta^y_jx_i\tag{2.7b} Δvij=ηδjyxi(2.7b) 可以看出,只要计算出式 ( 2.7 ) (2.7) (2.7)中的误差信号 δ k o \delta^o_k δko和 δ j y \delta^y_j δjy,权值调整量的计算推导即可完成。
对于输出层, δ k o \delta^o_k δko可展开为:
δ k o = − ∂ E ∂ n e t k = − ∂ E ∂ o k ∂ o k ∂ n e t k = − ∂ E ∂ o k f ′ ( n e t k ) (2.8a) \delta^o_k=-\frac{\partial E}{\partial {\rm net}_k}=-\frac{\partial E}{\partial o_k}\frac{\partial o_k}{\partial {\rm net}_k}=-\frac{\partial E}{\partial o_k}f'({\rm net}_k)\tag{2.8a} δko=−∂netk∂E=−∂ok∂E∂netk∂ok=−∂ok∂Ef′(netk)(2.8a) 对于隐层, δ j y \delta^y_j δjy可展开为: δ j y = − ∂ E ∂ n e t j = − ∂ E ∂ y j ∂ y j ∂ n e t j = − ∂ E ∂ y j f ′ ( n e t j ) (2.8b) \delta^y_j=-\frac{\partial E}{\partial {\rm net}_j}=-\frac{\partial E}{\partial y_j}\frac{\partial y_j}{\partial {\rm net}_j}=-\frac{\partial E}{\partial y_j}f'({\rm net}_j)\tag{2.8b} δjy=−∂netj∂E=−∂yj∂E∂netj∂yj=−∂yj∂Ef′(netj)(2.8b)
下面求式 ( 2.8 ) (2.8) (2.8)中网络误差 E E E对各层输出的偏导.
对于输出层,利用式 ( 2.1 ) (2.1) (2.1),可得: ∂ E ∂ o k = − ( d k − o k ) (2.9a) \frac{\partial E}{\partial o_k}=-(d_k-o_k)\tag{2.9a} ∂ok∂E=−(dk−ok)(2.9a) 对于隐层,利用式 ( 2.2 ) (2.2) (2.2),可得: ∂ E ∂ y j = − ∑ k = 1 l ( d k − o k ) f ′ ( n e t k ) w j k (2.9b) \frac{\partial E}{\partial y_j}=-\sum^l_{k=1}(d_k-o_k)f'({\rm net}_k)w_{jk}\tag{2.9b} ∂yj∂E=−k=1∑l(dk−ok)f′(netk)wjk(2.9b)
利用以上结果代入式 ( 2.8 ) (2.8) (2.8),如果激活函数全部利用单极性Sigmoid函数,即式 ( 1.6 ) (1.6) (1.6),可得:
δ k o = ( d k − o k ) o k ( 1 − o k ) (2.10a) \delta^o_k=(d_k-o_k)o_k(1-o_k)\tag{2.10a} δko=(dk−ok)ok(1−ok)(2.10a) δ j y = − [ ∑ k = 1 l ( d k − o k ) f ′ ( n e t k ) w j k ] f ′ ( n e t j ) = ( ∑ k = 1 l δ k o w j k ) y j ( 1 − y j ) (2.10b) \begin{aligned} \delta^y_j&=-\left[\sum^l_{k=1}(d_k-o_k)f'({\rm net}_k)w_{jk}\right]f'({\rm net}_j)\\ &=\left(\sum^l_{k=1}\delta^o_kw_{jk}\right)y_j(1-y_j)\tag{2.10b} \end{aligned} δjy=−[k=1∑l(dk−ok)f′(netk)wjk]f′(netj)=(k=1∑lδkowjk)yj(1−yj)(2.10b)
至此,两个误差信号已经推到完成,将式 ( 2.10 ) (2.10) (2.10)带回到式 ( 2.7 ) (2.7) (2.7),便得到了三层感知器的利用单隐层Sigmoid函数作激活函数的BP学习算法权值调整计算公式,即
{ Δ w j k = η δ k o y j = η ( d k − o k ) o k ( 1 − o k ) y j Δ v i j = η δ j y x i = η ( ∑ k = 1 l δ k o w j k ) y j ( 1 − y j ) x i (2.11) \left\{\begin{matrix}\Delta w_{jk}=\eta\delta^o_ky_j=\eta(d_k-o_k)o_k(1-o_k)y_j\tag{2.11}\\ \Delta v_{ij}=\eta\delta^y_jx_i=\eta\left(\sum^l_{k=1}\delta^o_kw_{jk}\right)y_j(1-y_j)x_i \end{matrix}\right. {Δwjk=ηδkoyj=η(dk−ok)ok(1−ok)yjΔvij=ηδjyxi=η(∑k=1lδkowjk)yj(1−yj)xi(2.11)
对于一般的多层感知器,设共有 h h h个隐层,按前向顺序各隐层神经元数分别记为 m 1 , m 2 , ⋯ , m h m_1,m_2,\cdots,m_h m1,m2,⋯,mh,各隐层输出分别记为 y 1 , y 2 , ⋯ , y h y^1,y^2,\cdots,y^h y1,y2,⋯,yh,各层权值矩阵分别记为 W 1 , W 2 , ⋯ , W h , W h + 1 \bm W^1,\bm W^2,\cdots,\bm W^h,\bm W^{h+1} W1,W2,⋯,Wh,Wh+1,则各层的权值调整计算公式为:
输出层 Δ w j k h + 1 = η δ k o y j h j = 0 , 1 , 2 , ⋯ , m h ; k = 1 , 2 , ⋯ , l \Delta w_{jk}^{h+1}=\eta\delta^o_ky^h_j\quad j=0,1,2,\cdots,m_h;\quad k=1,2,\cdots,l Δwjkh+1=ηδkoyjhj=0,1,2,⋯,mh;k=1,2,⋯,l 第 h h h隐层
Δ w i j h = η δ j h y i h − 1 = η ( ∑ k = 1 l δ k o w j k h + 1 ) f ′ ( n e t j h ) y i h − 1 i = 0 , 1 , 2 , ⋯ , m h − 1 ; j = 1 , 2 , ⋯ , m h \Delta w_{ij}^h=\eta\delta^h_jy^{h-1}_i=\eta\left(\sum^l_{k=1}\delta^o_kw_{jk}^{h+1}\right)f'({\rm net}_j^h)y^{h-1}_i\quad i=0,1,2,\cdots,m_{h-1};j=1,2,\cdots,m_h Δwijh=ηδjhyih−1=η(k=1∑lδkowjkh+1)f′(netjh)yih−1i=0,1,2,⋯,mh−1;j=1,2,⋯,mh 按以上规律逐层类推,则第一隐层权值调整计算公式:
Δ w p q 1 = η δ q 1 x p = η ( ∑ r = 1 m 2 δ r 2 w q r 2 ) f ′ ( n e t q 1 ) x p p = 0 , 1 , 2 , ⋯ , n ; q = 1 , 2 , ⋯ , m 1 \Delta w_{pq}^1=\eta\delta^1_qx_p=\eta\left(\sum^{m_2}_{r=1}\delta^2_{r}w^2_{qr}\right)f'({\rm net}_q^1)x_p\quad p=0,1,2,\cdots,n;q=1,2,\cdots,m_1 Δwpq1=ηδq1xp=η(r=1∑m2δr2wqr2)f′(netq1)xpp=0,1,2,⋯,n;q=1,2,⋯,m1
三层感知器的BP学习算法也可以写成向量形式。
对于输出层而言,设最后一隐层的输出 Y = ( y 0 , y 1 , y 2 , ⋯ , y i , ⋯ , y m ) T , δ o = ( δ 1 o , δ 2 o , ⋯ , δ k o , ⋯ , δ l o ) T \bm Y=(y_0,y_1,y_2,\cdots,y_i,\cdots,y_m)^T,\bm \delta^o=(\delta^o_1,\delta^o_2,\cdots,\delta^o_k,\cdots,\delta^o_l)^T Y=(y0,y1,y2,⋯,yi,⋯,ym)T,δo=(δ1o,δ2o,⋯,δko,⋯,δlo)T,则:
Δ W = η ( Y ( δ o ) T ) (2.12a) \Delta \bm W=\eta(\bm Y (\bm\delta^o)^T)\tag{2.12a} ΔW=η(Y(δo)T)(2.12a) 对于隐层而言,设输入层的输入 X = ( x 0 , x 1 , x 2 , ⋯ , x i , ⋯ , x n ) T , δ y = ( δ 1 y , δ 2 y , ⋯ , δ j y , ⋯ , δ m y ) T \bm X=(x_0,x_1,x_2,\cdots,x_i,\cdots,x_n)^T,\bm\delta^y=(\delta^y_1,\delta^y_2,\cdots,\delta^y_j,\cdots,\delta^y_m)^T X=(x0,x1,x2,⋯,xi,⋯,xn)T,δy=(δ1y,δ2y,⋯,δjy,⋯,δmy)T,则:
Δ V = η ( X ( δ y ) T ) \Delta\bm V=\eta(\bm X(\bm\delta^y)^T) ΔV=η(X(δy)T)
容易看出,在BP学习算法中,各层权值调整公式形式上是一样的,均有3各因素决定,即:学习率 η \eta η、本层输出的误差信号 δ \bm\delta δ以及本层输入信号 Y ( 或 X ) \bm Y(或\bm X) Y(或X)。