【算法竞赛学习】csoj：寒假第二场

前言

由于本人菜鸡，所以大多都是使用出题人的代码和思路
如有侵权，麻烦联系up删帖，本贴仅作为笔记记录

本篇大多是在吹水，技术方面可以直接看代码注释，思路在水文中，直接看代码也是可以看得懂的

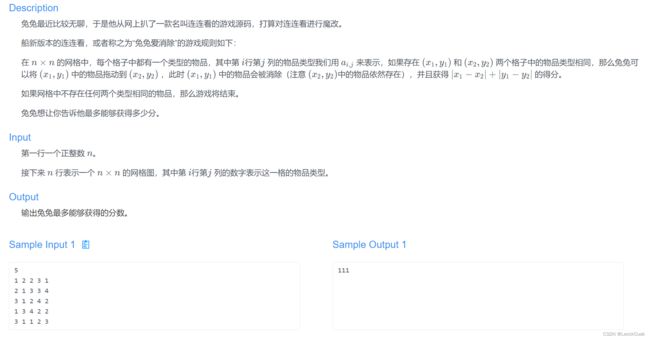
红包接龙

题目链接

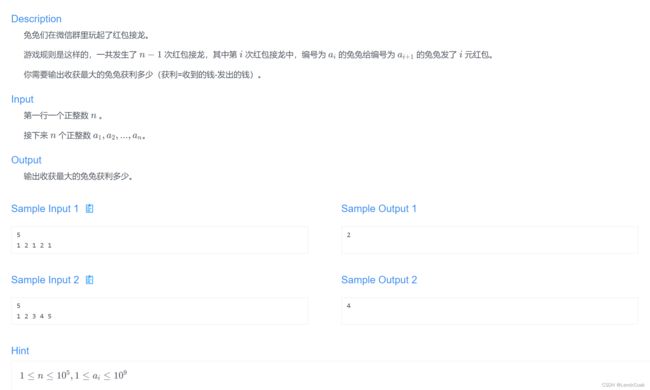
这题一看就知道离散化，最后只需要排序得到获利最大是多少就可以了，在处理上，因为ai比较大，如果像哈希表一样使用一个个存储的话，在a1=1和a2=1e9就需要遍历1e9次，大于1s了，所以使用离散化的话可以避免中间没必要的时间，不过我已经很久没有接触map了，使用起来很生疏导致有思路不知道怎么写，看了题解就一目了然了。

#include 
using namespace std;
int main() {
	ios::sync_with_stdio(0);//接触流绑定，加快cin和cout速度
	int n;
	cin>>n;
	vector<int>a(n);
	map<int,int>mp;
	for(auto &x:a)
	{
		cin>>x;
	}
	for(int i=0;i<n-1;i++)
	{
		mp[a[i]]-=i+1;
		mp[a[i+1]]+=i+1;
	}
	int ans=0;
	for(auto &[k,v]:mp)//k和v分别对应map的key和value
	{
		ans=max(ans,v);
	}
	cout<<ans<<endl;
	return 0;
}

最后一班

题目链接

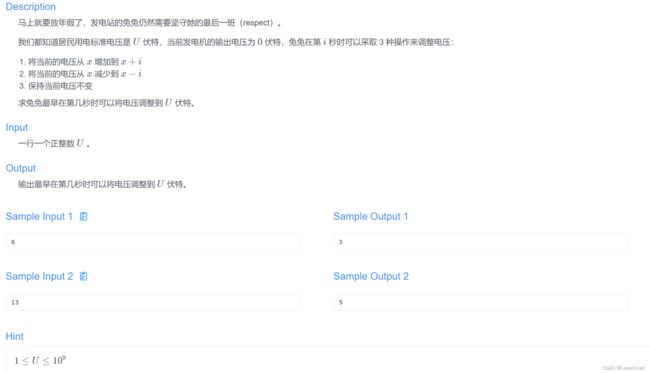
这题可以考虑到每秒都加压的话可以达到的最大电压，如果最大电压大于u的话就可以确定最小时间。

#include 
using namespace std;
typedef long long ll;
int main() {
	ios::sync_with_stdio(0);//接触流绑定，加快cin和cout速度
	int u;
	cin>>u;
	int ans=1;
	while(1)
	{
		if(ans*(ans+1)/2>=u)break;
		ans++;

	}
	cout<<ans<<endl;
	return 0;
}

勇者兔

题目链接

emm这题我当时没想出来，因为我总想找出一个办法先除去重叠最多的那个区间，然后再除去下一次重叠再多的，也是一种贪心算法，但是在重叠率的处理上遇到了麻烦，不过换一个思路会更加简单，可以看看出题人给的思路：

首先我们发现怪物在哪一行对我们做题没影响，假设每只怪物占据的列分别是 [l,r]。我们可以采取下面 的贪心策略：每次选择当前没死的怪中最小的 r， 在[r,r+w]宽度释放技能，消灭所有与这个区间有交集的怪。那么怎么知道一只怪是否被消灭了呢？我们发现每次释放技能 r+w 永远是严格递增的，我们可以维护一下上一轮的 r+w ，假设叫做 latest ，那么所有 l<=latest 的怪都是已经被消灭的。 可以对 r 进行排序或者使用优先队列来实现上面的贪心。
注：反过来每次选最大的 l 贪心也是一种正确的策略。
(P.S. 如果快速斩可以斜着放这题该怎么做？出题人不会）

出题人还提出斜着的问题，emm我自个认为可以像转换坐标系的方法去作垂足应该可以转换成与该题一样的方法吧，不过我也没做过这种题，没写过代码，有其他思路的也欢迎在评论区评论。
看完大家应该也知道这题怎么做了吧，来看看代码吧。

#include 
using namespace std;
typedef long long ll;
int main() {
	ios::sync_with_stdio(0);//接触流绑定，加快cin和cout速度
	int n,w;
	cin>>n>>w;
//	priority_queue,vector>,greater>>q;//小顶堆
	priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>>q;//这种写法也是一样的
	while(n--)
	{
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		q.push({d,b});//注意d是上面的一条边，b是下面的一条边，选择d作为排序的主键可以最大化除去怪兽

	}
	int ans=0;
	int top=0;
	while(!q.empty())
	{
		auto [b,t]=q.top();
		q.pop();
		if(t<top)continue;
		top=b+w;
		ans++;
	}
	cout<<ans<<endl;
	return 0;
}

兔兔爱消除

题目链接

我们发现对每种类型的物品，会从 cnt 个物品开始，每次消除一个，直到剩下 1 个为止，如果把这个过程反过来：从 1 个物品开始，每次添加一个物品，直到物品个数达到 cnt 。发现这就是一个最大生成树的过程。所以初始化一下整张图，跑一遍最大生成树即可。

当时我并没有想到，看了出题人的思路才明白，我还是太菜了！！！

最大生成树算法和最小生成树算法几乎一样，用Krushal算法求最小生成树的时候，每一次选择的边是最大的边，然后再去判断这条边是否可以加入（成环），那么这就是最大生成树的求取方法了。

#include
using namespace std;
typedef long long ll;
struct edge{
	int u,v,w;
	edge(int u,int v,int w):u(u),v(v),w(w){}
};

int main(){
	ios::sync_with_stdio(0);//提高流速度
	int n;
	cin>>n;
	vector<vector<int>>a;
	vector<edge>edges;
	for(int i=0;i<n;i++)
	{
		vector<int>row(n);
		for(auto &x:row)
			cin>>x;
		a.push_back(row);

	}
	auto id=[&](int i,int j){//匿名函数
		return i*n+j;
	};
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			for(int ii=0;ii<n;ii++)
			{
				for(int jj=0;jj<n;jj++)
				{
					if(a[i][j]==a[ii][jj]&&i!=ii&&j!=jj){
						edges.push_back({id(i,j),id(ii,jj),abs(i-ii)+abs(j-jj)});
					}
				}
			}

		}
	}
	vector<int>father(n*n);
	iota(father.begin(), father.end(), 0);
	auto find=[&](int x){//并查集:查询，while实现路径压缩
		while(x!=father[x])x=father[x]=father[father[x]];//此处需要用while，而不能用if，重点在拓展部分（并查集）讲解为什么不能用if
		return x;
	};
	sort(edges.begin(),edges.end(),[](const edge &a,const edge &b){
		return a.w>b.w;
	});//自定义比较函数
	ll ans=0;
	for(auto &e:edges)
	{
		ll x=find(e.u),y=find(e.v);
		if(x!=y)//是否成环判断
		{
			ans+=e.w;
			father[x]=y;//并查集：合并。将y作为x的父节点，此处x作为y的父节点也是可以的
		}
	}
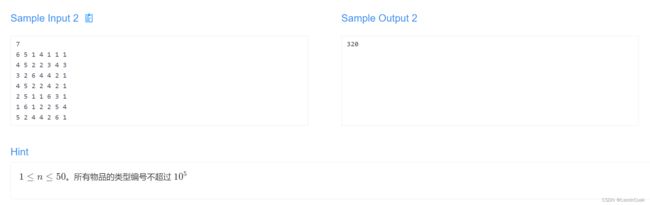
	cout<<ans<<endl;


}

吃席兔

题目链接

这道题花费了我不少时间呢！这道题用到了树形dp，所以连简单dp都不太会的我去学了树形dp（可以看看拓展知识的参考链接），这题难度确实比较大，但是硬着头皮较真下去还是能学会不少东西的！！！

先来看看出题人的思路吧！

我们假设这是一个 1 为根的有根树。先思考一个简化版的问题：如果第 i 只兔子只能往自己的子树内部移动，那么第 i 只兔子能否吃席？ 令 $cn{t}_i$ 表示子树 i 中有多少只兔子家有办席。我们发现只要满足下面 3 个条件之一，第 i 只兔子就能吃席：

1. 第 i 只兔子家有办席
2. 有个与 i 直接相连的兔子家有办席
3. 存在 i 的某个子节点 j ，$cn{t}_j$ >=2 且 j 能吃到席 ( 一定有办法先走到 j 再模仿 j 的策略)

那么完整版问题怎么做呢？从子树的答案转移到整棵树的答案是树dp 比较经典的一个套路，我们再进行 一遍 dfs ，第二遍 dfs 时把父节点当成当前点的子节点，模仿第一遍 dfs 进行转移即可。

出题人的思路咋一看其实有些难懂，我也花了不少时间琢磨，在这里择要地解释一下。

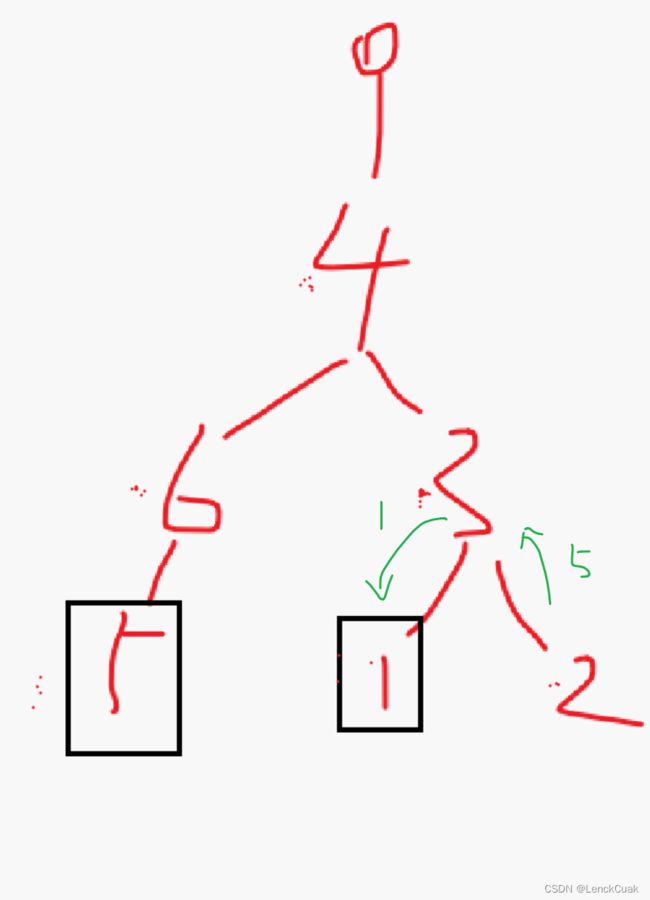
前面2个条件应该都能理解，第三个条件是什么意思呢？可以看看下面这个图：

当i为1，i的子节点j为8，$cn{t}_j>=2$， 则i可以在第一次选择9走一步到2，由于每次选择不能选择上一步相同的兔子，则第二步选择10走一步到4，第三步再次选择9，因为第三步的上一步是选择10，而不是9，所以第三步可以选择9走一步到5，第四步选择10到6，第5步选择9到7，第6步选择10到8，第7步选择9到9，这样兔子i就可以吃到席了。

完整版就可以看代码知道两次dfs的作用了。

#include 
using namespace std;
typedef long long ll;
int main()
{
	ios::sync_with_stdio(0);
	int n;
	cin >> n;
	vector<int> a(n), ok(n), cnt(n);//a[i]表示第i只兔子摆席，ok[i]表示第i只兔子可以吃到席，cnt[i]表示子树 i 中有多少只兔子家有办席
	vector<vector<int>> g(n);//n个节点的边，g[i]表示与i相邻的点
	for (auto &x : a)
		cin >> x;
	for (int i = 1, u, v; i < n; i++)
	{
		cin >> u >> v;
		--u;
		--v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	function<void(int, int)> dfs = [&](int u, int fa)//匿名函数
	{
		if (a[u])//如果u摆席，则u可以吃到席
			ok[u] = 1, cnt[u] = 1;
		for (int v : g[u])
			if (v != fa)
			{
				dfs(v, u);//从叶子节点开始
				if (cnt[v] > 1)//如果子树v的摆席>1，则u能否吃到席就得看v能否吃到席，如果v吃不了席，那么u也别想吃。
					ok[u] |= ok[v];
				if (a[v])//如果v摆席，那u当然可以吃到席 ，因为只有一步
					ok[u] = 1;
				cnt[u] += cnt[v];
			}
	};
	dfs(0, 0);
	function<void(int, int)> dfs2 = [&](int u, int fa)
	{
		if (u && cnt[0] - cnt[u] > 1)//将u作为父节点，由于cnt[0]和cnt[u]都是记录自己子树的摆席数，是同一个方向的，相减就可以朝相反方向移动
			ok[u] |= ok[fa];//如果父节点可以吃席，那么u也可以吃席，如果u本来就可以吃席，而父节点不能吃席，u自然还是可以吃席的，所以这也是用|的原因
		if (a[fa])
			ok[u] = 1;//如果父节点摆席，那么u还是可以吃席的，只有一步距离
		for (int v : g[u])
			if (v != fa)
			{
				dfs2(v, u);//从顶部到底部遍历
			}
	};
	dfs2(0, 0);
	for (auto &x : ok)
		cout << x << " \n"[&x == &ok.back()];//[&x == &ok.back()]的作用是以空格作为输出元素的分隔符，如果输出完毕将以\n结尾。
	return 0;
}

单纯看代码是很难理解的，可以自己画一下，对于样例的图示：

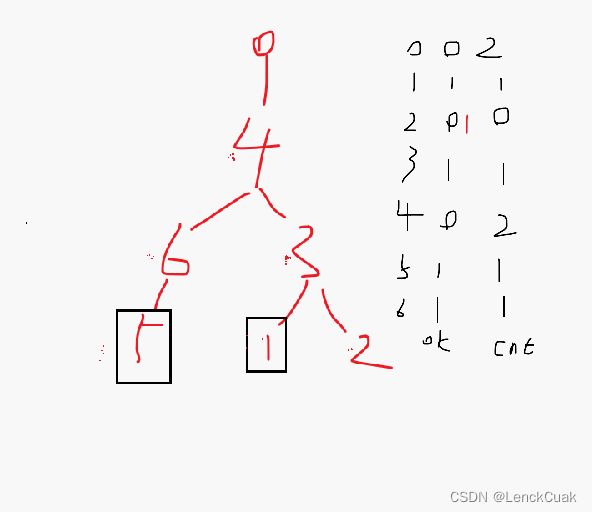
黑色框住的是摆席的兔子编号，因为是按照代码来画的图，所以编号都是从0开始的，而出题人在讲思路时是1开始的，明白就可以了。图右最左侧的一列数字表示节点编号，编号2的ok[2]的黑色的0是在第一次dfs时的值，在第二次dfs时ok[2]改为1。原因如下图：

或者可以用代码中转换父节点的思路：

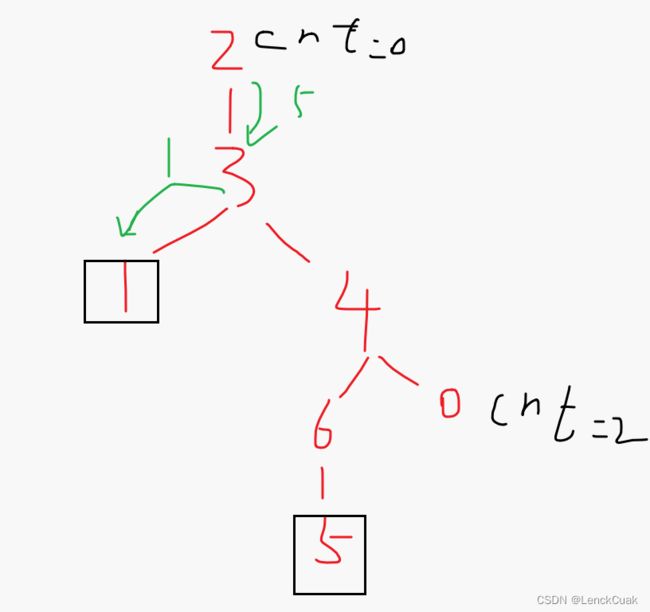
其实是一样的，主要是cnt[0]-cnt[u]这块搞懂转换方向就可以了。
绿色箭头旁边的绿色数字表示选择摆席兔子编号。

知识拓展

std::greater | 堆优化

对于顺序容器数组、vector等：

sort(arr.begin(), arr.end(), greater<int>()); //降序排序

对于关联式容器，如优先队列、堆，使用

priority_queue<int>  //默认降序队列，大顶堆

priority_queue<int,vector<int>,less<int>> //单个元素。降序队列，大顶堆

priority_queue<int,vector<int>,greater<int>>  //单个元素。升序队列，小顶堆

priority_queue <pair<int, int>, vector<pair<int, int> >, greater<>> pq;//堆优化
pair<dist，结点编号>，dist小的在队列中靠前。

Dijkstra堆优化 | priority_queue , vector >, greater<>>题目

参考

C++ std::greater用法及代码示例

Dijkstra堆优化 | priority_queue , vector >, greater<>>

iota函数

template <class ForwardIterator, class T>
  void iota (ForwardIterator first, ForwardIterator last, T val)
{
  while (first!=last) {
    *first = val;
    ++first;
    ++val;
  }
}

参考

https://blog.csdn.net/u014786409/article/details/94634855

并查集

并查集的查询操作，这个操作实现了路径压缩

auto find=[&](int x)
{
	while(x!=father[x])x=father[x]=father[father[x]];
	return x;
}

为什么不能使用if呢？有人可能会问，那可能是因为他们看到了x=father[x]这个赋值操作，while里的x!=father不就没有必要使用while了吗？

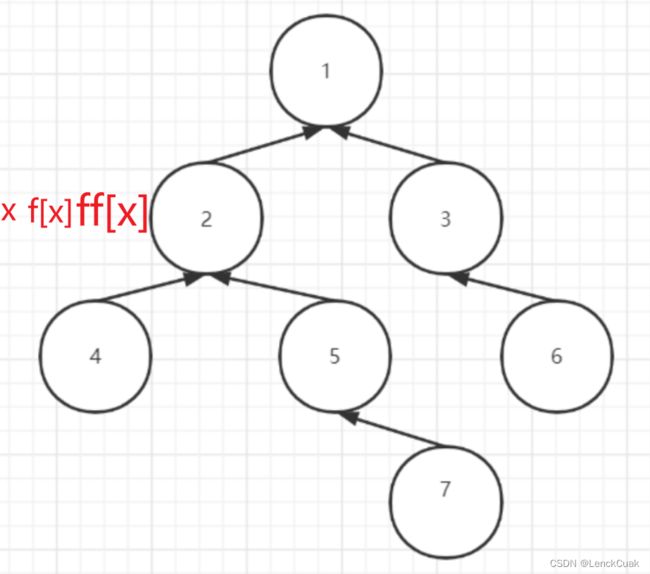
但仔细想想其实并不是，可以看看这个图：
假设我们的x是7，那么我使用f[x]表示father[x],ff[x]表示father[father[x]]。

经过第一步while操作后：

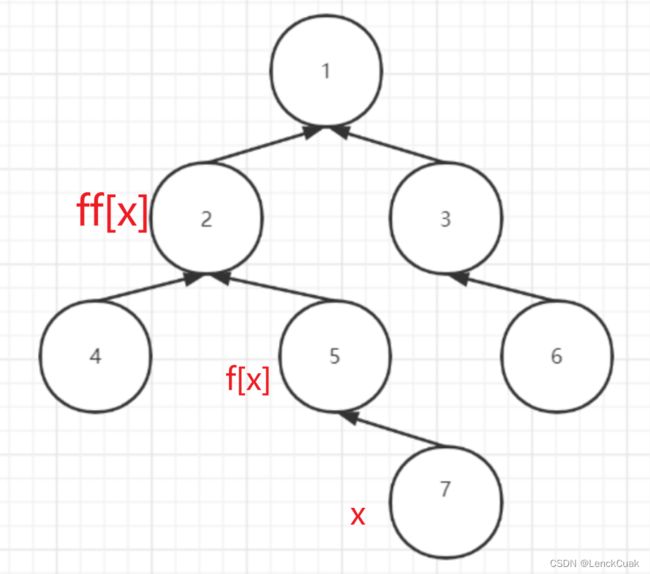
此时确实是x=father[x]了，但请注意此时的x是之前的x，或者可以这样表示:

再将 x`=x

但在下一步while判断的时候，x!=father[x]了，所以这个while可以实现路径压缩，变成下图这个样子。

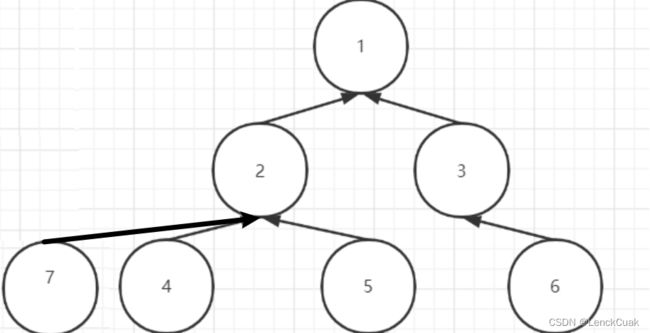
参考

算法笔记：并查集（包含其他路径压缩方法）

并查集while(x!=father[x])x=father[x]=father[father[x]];详解

并查集详解，图片出处

sort自定义函数

sort(edges.begin(),edges.end(),[](const edge &a,const edge &b){
		return a.w>b.w;
	});//自定义比较函数

这个写法挺特别的，目前没有找到为什么可以这么写的原因，暂且记录下来，其余写法见参考链接。

参考

sort自定义比较详解

树形dp

这里没有什么内容，主要看参考资料就可以了！！！

参考

动态规划入门——动态规划与数据结构的结合，在树上做DP
【算法学习笔记】动态规划与数据结构的结合，在树上做DP

使用auto时控制分隔符

由于使用auto时没有直接使用for(int i;;)等等那么方便地控制分隔符，那么这个代码就可以控制分隔符：

for (auto &x : ok)
		cout << x << " \n"[&x == &ok.back()];//[&x == &ok.back()]的作用是以空格作为输出元素的分隔符，如果输出完毕将以\n(\n表示一个字符)结尾。

这么解释有些难以理解吧？

可以用更简单的方式展示：

for (auto &x : ok)
		cout << x << "as"[&x == &ok.back()];//[&x == &ok.back()]的作用是以a作为输出元素的分隔符，如果输出完毕将以s结尾。