【DL】4个问题的思考与解决

对这个文章中问题的思考，点击跳转

1.改变数据集的依据是什么？

一般思路：分析数据集，选择合适模型

2.怎么分辨数据集的数据是否线性可分？

最简单的情况是数据向量是一维二维或者三维的，我们可以把图像画出来，直观上就能看出来。
多维情况可以先PCA降维，在将前几行列画图画出来。
降维是对数据高维度特征的一种预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。
**主成分分析（PCA）是一种分析、简化数据集的技术。**主成分分析经常用于减少数据集的维数，同时保持数据集中的对方差贡献最大的特征。通俗理解：就是找出一个最主要的特征，然后进行分析。
PCA 思想

• 去除平均值 计算协方差矩阵
• 计算协方差矩阵的特征值和特征向量
• 将特征值排序
• 保留前N个最大的特征值对应的特征向量
• 将数据转换到上面得到的N个特征向量构建的新空间中（实现了特征压缩）

具体的算法流程
输入：n维样本集D=(x(1),x(2),…,x(m))，要降维到的维数n.
输出：降维后的样本集D′

1. 对所有的样本进行中心化：x(i)=x(i)−1m∑mj=1x(j)
2. 计算样本的协方差矩阵XXT
3. 对矩阵XXT进行特征值分解
   4）取出最大的n’个特征值对应的特征向量(w1,w2,…,w′n), 将所有的特征向量标准化后，组成特征向量矩阵W。
   5）对样本集中的每一个样本x(i),转化为新的样本z(i)=WTx(i)
4. 得到输出样本集D′=(z(1),z(2),…,z(m))

协方差矩阵

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度，其中，方差的计算公式为

其中，n表示样本量，
在此基础上，协方差的计算公式被定义为

PCA 优缺点：
优点：降低数据的复杂性，识别最重要的多个特征。
缺点：不一定需要，且可能损失有用信息。
适用数据类型：数值型数据。

PCA的思想是将n维特征映射到k维上（k 实例：

#PCA降维

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  #3D绘图教程   3D曲面和散点的绘制用的都是mpl_toolkits库的mplot3d模块中的Axes3D来完成
#from sklearn.datasets.samples_generator import make_blobs
from sklearn.datasets import make_blobs  #sklearn中的make_blobs函数主要是为了生成数据集的

 
import sys
sys.path.append(r'D:\zhangzhe\Postgraduate\lab\Myself')
# 样本10000个，特征维度3
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3, 3, 3], [0, 0, 0], [1, 1, 1], [2, 2, 2]],
                  cluster_std=[0.2, 0.1, 0.2, 0.2], random_state=9)
print(X,y)

"""
n_features表示每一个样本有多少特征值
n_samples表示样本的个数
centers是聚类中心点的个数，可以理解为label的种类数
random_state是随机种子，可以固定生成的数据
cluster_std设置每个类别的方差
"""
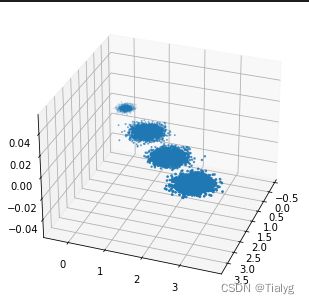
# 画图
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o')
plt.show()

# 计算特征值和特征向量 n                              
eigvalue, eigvector = np.linalg.eig(np.cov(X.T))   #计算方阵的特征值和右特征向量。
print(eigvalue)
print(eigvector)


# 获取第一个和第三个特征
a = np.hstack((eigvector[:, 0].reshape(3, -1), eigvector[:, -1].reshape(3, -1)))
print(a)
X = X - X.mean(axis=0)
X_new1 = X.dot(a)
print(X_new1)


fig = plt.scatter(X_new1[:, 0], X_new1[:, 1], marker='o')
plt.show()

降维：

3.如何根据模型选择激活函数？

• 用于分类器时，Sigmoid函数及其组合通常效果更好。
• 由于梯度消失问题，有时要避免使用sigmoid和tanh函数。
• ReLU函数是一个通用的激活函数，目前在大多数情况下使用。
• 如果神经网络中出现死神经元，那么PReLU函数就是最好的选择。
• 注：ReLU函数只能在隐藏层中使用。
• 死神经元：尽管 ReLU 解决了因激活函数导数的绝对值小于 1，在反向传播连乘的过程中迅速变小消失至 0 的问题，但由于它在输入为负的区段导数恒为零，而使得它对异常值特别敏感。这种异常值可能会使 ReLU 永久关闭，而杀死神经元。

一点经验：可以从ReLU函数开始，如果ReLU函数没有提供最优结果，再尝试其他激活函数。

常见激活函数：

4.别人论文中学习率一般是怎么设置的？

最常见的方法：使用学习率规划器
为了同时保证训练速度和收敛范围，目前最常用的方法就是动态衰减神经网络的学习率（可以保持固定的Batch Size，对训练机器显存的利用和规划有利）。
在训练过程中，最简单的调整学习率的方法就是让学习率随着时间的推移而不断衰减。在训练开始时，我们通常使用较大的学习率来让模型快速达到较好的性能，随后通过衰减学习率使模型权重更好地逼近最优的配置。

两个易于使用的学习率规划器：

• 学习率随训练批次连续衰减。
• 学习率在特定的批次衰减，即阶梯式衰减学习率。

详细点这里

一个很不错的文章

LearningRate = LearningRate / (1 + decay * epoch)

衰减系数decay
Decay = LearningRate / Epochs

例如：
我们设置一个较高的学习率0.1作为初始值，设定训练的批次数（epochs）为50，根据上面的公式计算得到衰减系数为0.1/50=0.002。

• 提高初始学习率。因为学习率一般会随着训练批次的增加而降低，所以不妨让学习率从一个较高的水平开始下降。较大的学习率可以使模型在初始训练时权重有更大的变化，有助于后续低学习率调优时收敛至更优的权重范围。
• 使用大的动量系数。使用大的动量系数可以保证在你的学习率衰减得比较小时，优化算法还可以使模型权重在正确的方向上以较快的速度收敛。
• 尝试不同的学习率计划器。因为现在还没有理论明确地指出什么情况下应该使用什么样的学习率规划器，所以你需要尝试各种不同的配置来寻找最适合你当前问题的计划器配置。你可以按照指数规律划分学习率规划器的参数，也可以根据模型在训练集/测试集上响应的结果自适应地调整学习率规划器参数。