【论文笔记 - 图像生成 - CVPR2019】Unpaired Person Image Generation with Semantic Parsing Transformation

Ref:

1. 先前工作以及补充

2. 本文工作（本阅读笔记的参考论文）

3. 解读1

4. 解读2

原论文是关于 2019 年的 CVPR 工作的延伸和补充（同一作）

现有工作的特点：

• 姿态引导的图像生成任务一般是在有监督下完成的，结果虽然不错，但是监督学习必须有成对的图像组成训练数据集。（成对：同一个人，同样的外观，但是姿态不同）

• 自监督方法，无法有效的同时建模空间和外观转换，结果不够理想。

• 虽然目前的方法都考虑到将图像分解成多个因素（背景，前景，形状，外观），但忽略了非刚性的人体变化以及服装造型等因素，导致了生成图像质量较差。

• 在给定条件图像的情况下，主要关注于呈现外观一致的前景，而不考虑背景合成。

作者认为的难点：

• 由于人体的非刚性特性，对于基于卷积的网络，通常很难对空间非对齐的身体部位进行变换。
• 服装属性，如服装类型、纹理等，在生成过程中难以保存，但是这些服装属性对人类的视觉感知很重要。
• 姿态变化会导致背景区域缺失，生成上下文相关的背景并与前景无缝地缝合是很麻烦的。
• 缺乏成对训练数据，无法为建立有效的训练目标（测试的时候，姿态和源图像姿态不同）提供信息。

本文的工作：

• 为了解决基于非成对数据的人物图像生成问题，作者将其分解为两个子任务，即语义解析变换 $H_S$ 和外观生成 $H_A$。
• 在训练过程中使用了伪标签，并证明了网络的端到端训练可以实现更好的语义映射预测，然后帮助改善最终结果。
• 对于外观生成，作者考虑分别生成前景和背景。引入了一个背景生成网络来预测（由姿态变化导致的）缺失背景的区域，并生成逼真的结果。

Methods

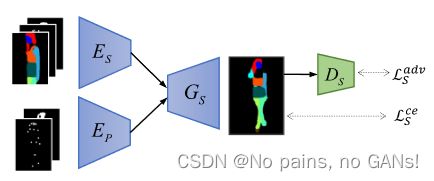
本文模型的主体框架是基于循环一致性的，分为了目标语义生成器 $H_S$ 和外观生成器 $H_A$，如下所示，（测试的时候只需要一半就行）

1. Semantic Parsing Transformation（$H_s$）

1.1 伪标签

训练语义生成网络 $G_S$ 是为了对不同姿态下的空间语义变形进行建模。由于服装纹理与语义图没有关联，不同服装细节的人可能共享相似的语义图。因此，可以从训练图像中创建语义映射对，方便模型训练。

对于给定的 $S_{p_s}$，需要在训练集中找到一个与其处于不同姿态但服装类型相同的语义映射 $S_{p_t^{\ast }}$。然后以 $p_t^{\ast }$ 作为 $S_{p_s}$ 作为目标姿态，以 $S_{p_t^{\ast }}$ 作为 pseudo ground truth。如上图所示，将人体分为十部分，可以用一组二进制掩码 ${\left\{B^j\right\}}_{j=1}^{10}\left(B^j\in {\mathbb{R}}^{H\times W}\right)$ 表示。

具体来说，是要找到一个 $S_p$ 能够使相同语义解析区域的差别最小，来作为 $S_{p_t^{\ast }}$，通过求解下式来获得伪标签，

$S_{p_t^{\ast }}=\arg {\min }_{S_p}\frac{1}{n}{\sum }_{j=j_1}^{j_n}\frac{1}{|B_{p_s}^j|}{\Vert B_{p_s}^j\otimes S_{p_s}-f_j\left(B_p^j\otimes S_p\right)\Vert }_2^2$

其中，$\left\{j_1,\dots ,j_n\right\}$ 表示对 $S_p$ 和 $S_{p_s}$ 都有效的掩码索引。$\otimes$ 是 element-wise 的乘法运算符。用仿射变换 $f_j(\cdot )$ 对两个身体部分进行对齐，其可以根据对应掩码的四个角，然后最小化最小二乘误差来计算，即下式，

${\min }_{f_j(\cdot )}{\Vert f_j\left(B_p^j\right)-B_{p_s}^j\Vert }_2^2$

伪标签搜索时，排除了非常相似的姿态。在实验中，从训练集中随机选择 N (N=500) 张图像作为候选伪标签，然后进行如上所述的伪标签生成。

• 通过随机选择伪标签候选，避免了伪标签生成时找到真实标签的情况。
• 只采用部分数据集，加快了搜索过程。

（

这一部分，感觉每个人体部分都计算仿射变换系数，会忽略人体各部分的比例问题。

夸张一点，有一张语义解析图，手很短腿很长，但是候选图里大都是正常情况，经过仿射变化后，会忽略这个大小的关系，只能够保证比例关系，而且是单一人体部分的比例。这样一张正常人的解析图就匹配上了，但很明显，是不对的。

）

1.2 损失

有交叉熵损失和对抗损失，

有了成对数据 $\left\{S_{p_s},{\mathbf{p}}_s,S_{p_t^{\ast }},{\mathbf{p}}_t^{\ast }\right\}$，语义生成网络可以有监督的进行训练。利用交叉熵损失 ${\mathcal{L}}_S^{ce}$ 来约束语义解析图变换的像素级精度，并在姿态掩码 $M_{p_t^{\ast }}$ 的基础上赋予人体比背景更大的权重，

${\mathcal{L}}_S^{ce}=-{\Vert S_{p_t^{\ast }}\otimes \log \left({\tilde{S}}_{p_t^{\ast }}\right)\otimes \left(1+M_{p_t^{\ast }}\right)\Vert }_1$

2. Appearance Generation ($H_A$)

在该模块中，作者利用条件图像 $I_{p_s}$ 和前一个模块生成的目标姿态下的语义解析图 ${\tilde{S}}_{p_t}$，为输出图像 ${\tilde{I}}_{p_t}\in {\mathbb{R}}^{3\times H\times W}$ 合成纹理。

作者将整个目标图像的生成分为前景 ${\tilde{I}}_{p_t}^F$ 和背景 ${\tilde{I}}_{p_t}^B$ 两部分，即如下公式，

${\tilde{I}}_{p_t}={\tilde{I}}_{p_t}^F\otimes \Omega \left({\tilde{S}}_{p_t}\right)+{\tilde{I}}_{p_t}^B\otimes \left(1-\Omega \left({\tilde{S}}_{p_t}\right)\right)$

其中，$\otimes$ 表示 element-wise 乘法，$\Omega (\cdot )$ 是获得前景掩码。

2.1 Foreground Generation

前景生成网络包括，

• 外观编码器 $E_A^F$ 提取条件图像 $I_{p_s}$ 的前景特征，

• 语义映射编码器 $E_S^{{}^{\prime }}$ 编码先前得到的目标姿态的语义解析图 ${\tilde{S}}_{p_t}$，

• 与语义生成网络不同的是，前景生成器 $G_A^F$，采用 deformable skips 来更好地处理空间变形。

${\tilde{I}}_{p_t}^F=G_A^F\left(E_A^F\left(I_{p_s},S_{p_s},{\mathbf{p}}_s\right),E_S^{\prime }\left(S_{p_t},{\mathbf{p}}_t\right)\right)$

2.2 Background Generation

为了保持输入图像的背景，采用 basic U-Net 作为背景生成网络，该网络由背景编码器 $E_A^B$ 和背景生成器 $G_A^B$ 组成，

${\tilde{I}}_{p_t}^B=G_A^B\left(E_A^B\left(I_{p_s}\otimes \Omega \left(S_{p_s}\right)\right)\right)$

之前有提到，人体姿势的变化会导致输出图像的背景区域缺失。为了生成自然图像，作者希望背景生成网络能够根据背景进行修复。然而，由于原始数据缺乏对 ground truth 背景图像的监督，使得网络很难正确地渲染缺失区域，尤其是在背景纹理复杂的情况下。为了解决这个问题，作者还引入了额外的辅助数据集，并引入重构损失。

${\mathcal{L}}_B^{rec}={\Vert I_{aux}-G_A^B\left(E_A^B\left(I_{aux}\otimes \Omega \left(S_{p_s}\right)\right)\right)\Vert }_2^2$

(损失比较常规，不多介绍)