自动驾驶感知——物体检测与跟踪算法|4D毫米波雷达
文章目录
- 1. 物体检测与跟踪算法
-
- 1.1 DBSCAN
- 1.2 卡尔曼滤波
- 2. 毫米波雷达公开数据库的未来发展方向
- 3. 4D毫米波雷达特点及发展趋势
-
- 3.1 4D毫米波雷达特点
-
- 3.1.1 FMCW雷达角度分辨率
- 3.1.2 MIMO ( Multiple Input Multiple Output)技术
- 3.2 4D毫米波雷达发展趋势
-
- 3.2.1 芯片级联
- 3.2.2 专用芯片
- 3.2.3 标准芯片+软件提升
- 声明
1. 物体检测与跟踪算法
1.1 DBSCAN
DBSCAN: Density Based Spatial Clustering of Applications with Noise;
DBSCAN是基于密度的聚类方法,对样本分布的适应能力比K-Means更好。
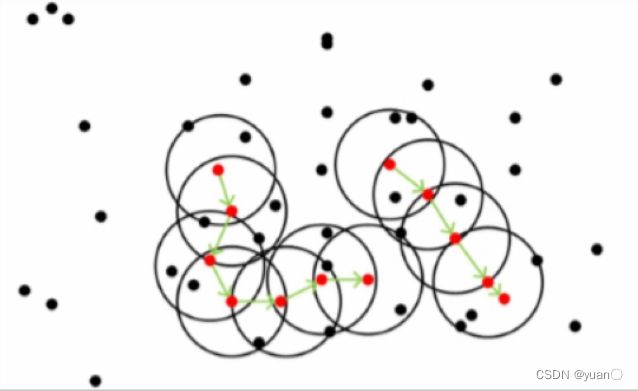
黑色的点是非核心对象
注意:距离的度量不限于点的空间距离,还可以是其它点特征,比如速度、反射强度等
基本思路
假定类别可以通过样本分布的紧密程度决定,通过将紧密相连的样本分为一类,得到不同的聚类类别。
基本概念
- ( ε , M i n P t s ) (\varepsilon ,MinPts) (ε,MinPts):用来描述邻域的密度;
- ε \varepsilon ε:描述了某一样本的邻域距离阈值;
- M i n P t s MinPts MinPts:描述了邻域中的最小样本数。
- 核心对象:对于任一样本,其邻域至少包含MinPts个样本。
算法流程
- 找到所有的核心对象
- 对于每一个未处理的核心对象,生成新的聚类;
- 搜索其 ε \varepsilon ε邻域,将 ε \varepsilon ε邻域中的点加入该聚类;
- 不断重复以上步骤
DBSCAN的详细讲解可以参考这篇博文DBSCAN详解
K-Means
K-Means与DBSCAN 的对比
K-Means
- 需要手工指定cluster的数量
- 所有点都进行聚类,不会去除outlier
- 各个方向同等重要,只适合于球形的cluster
- 具有随机性,每次运行结果不一致
DBSCAN
- 不需要指定cluster个数
- 可以排除outlier
- 对样本分布的适应性更好
- 每次运行结果是一致的
1.2 卡尔曼滤波
本节只是对卡尔曼滤波的应用进行介绍,具体原理可见这篇博客——详解卡尔曼滤波原理以及https://www.kalmanfilter.net/

基本概念
以一维雷达测距为例,假设速度恒定,
系统状态 x t x_t xt: t t t时刻飞机的航程;
测量值 z t z_t zt:雷达测距结果;
系统状态的估计值 x ⃗ t , t {\vec x_{t,t}} xt,t: t t t时 刻 x x x的估计值(根据 z z z估计) ;
系统状态的预测值 x ⃗ t + 1 , t {\vec x_{t + 1,t}} xt+1,t: t + 1 t+1 t+1时刻 x x x的预测值(根据速度预测)



雷达目标跟踪:多目标.
Tracking-by-Detection
- 由聚类算法在单帧点云得到目标输出;
- 提取目标的特征,包括统计特征(比如点位置的均值,方差等)和运动特征(比如速度和加速度等) ;
- 根据特征计算当前帧的检测目标(detections)与已跟踪的多个目标(tracks)的相似度;
- 按照相似度将de tections分配给tracks;
- 卡尔曼滤波更新tracks的状态参数(位置、速度等)。
2. 毫米波雷达公开数据库的未来发展方向
未来发展方向
-
多模态数据
➢包括同步的图像,激光雷达等数据,用来进行多传感器融合的研究。 -
多数据类型
➢包括ADC数据,RAD数据,点云数据等,为不同层次的算法研究和实际应用提供支持。 -
360度视场
➢需要多个雷达配合完成,以满足多种自动驾驶应用的需求。8.01。 -
大规模数据
➢一般来说,至少要有超过10万帧的不同场景,不同天气条件下采集的数据。 -
丰富的标注信息
➢物体级:类别,位置,大小,方向,分割的mask
➢场景级:语义信息,比如free space, occupied space等。
3. 4D毫米波雷达特点及发展趋势
3.1 4D毫米波雷达特点
4D指的是距离(Range) ,水平角度(Azimuth) ,俯仰角度( Elevation)和速度(Doppler) 。一般来说, 4D 毫米波雷达的角度分辨率相对较高,因此也经常被称为4D成像雷达。
4D毫米波雷达的两个主要特点是:
1)可以测量高度的信息;
2)角度分辨率较高。
为了更好的理解这两点,首先要了解FMCW雷达角度分辨率的依赖因素,以及为了增加角度分辨率所采用的MIMO机制。
3.1.1 FMCW雷达角度分辨率
想要测量目标的方位角,至少需要两个接收天线(RX).可以通过相位差来求得方位角 θ = sin − 1 ( ω λ 2 π d ) \theta = {\sin ^{ - 1}}(\frac{{\omega \lambda }}{{2\pi d}}) θ=sin−1(2πdωλ)

在有多个接收天线时,每个接收信号与前一个接收信号之间的相位差都是 ω \omega ω。以下图为例,假设有4个接收天线,以第一个接收天线为基准,4个接收信号的相位差分别为0, ω \omega ω,2 ω \omega ω,3 ω \omega ω。这个序列信号的变化频率就是 ω \omega ω,因此我们通过FFT来提取这个分量(也就是角度FFT)。

如果场景中存在多个目标,而且其距离和速度都相同,那么雷达能够区分这些目标的最小角度差称之为角度分辨率。假设有以下场景,场景中有两个目标,其方位角分别为 θ \theta θ和 θ + Δ θ \theta+\Delta\theta θ+Δθ,对应的相位差分别为 ω 1 \omega_1 ω1和 ω 2 \omega_2 ω2。 ω 1 = 2 π λ d sin ( θ ) {\omega _1} = \frac{{2\pi }}{\lambda }d\sin (\theta ) ω1=λ2πdsin(θ) ω 2 = 2 π λ d sin ( θ + Δ θ ) {\omega _2} = \frac{{2\pi }}{\lambda }d\sin (\theta + \Delta \theta ) ω2=λ2πdsin(θ+Δθ) Δ ω = ω 2 − ω 1 = 2 π d λ ( sin ( θ + Δ θ ) − sin ( θ ) ) \Delta \omega = {\omega _2} - {\omega _1} = \frac{{2\pi d}}{\lambda }(\sin (\theta + \Delta \theta ) - \sin (\theta )) Δω=ω2−ω1=λ2πd(sin(θ+Δθ)−sin(θ))因为 sin ( θ ) \sin(\theta) sin(θ)的导数为 cos ( θ ) \cos(\theta) cos(θ),所以可得 Δ ω = 2 π d λ ( cos ( θ ) Δ θ ) \Delta \omega = \frac{{2\pi d}}{\lambda }(\cos (\theta )\Delta \theta ) Δω=λ2πd(cos(θ)Δθ)根据傅里叶变换理论,N点的FFT可以区分的频率分量最小为2π/N,这里的N就是接收天线的个数。这样我们就可以得到可以分辨的最小角度差,也就是角度分辨率。 Δ ω > 2 π N \Delta \omega > \frac{{2\pi }}{N} Δω>N2π ⇒ 2 π d λ ( cos ( θ ) Δ θ ) > 2 π N \Rightarrow \frac{{2\pi d}}{\lambda }(\cos (\theta )\Delta \theta ) > \frac{{2\pi }}{N} ⇒λ2πd(cos(θ)Δθ)>N2π ⇒ Δ θ > λ N d cos ( θ ) \Rightarrow \Delta \theta > \frac{\lambda }{{Nd\cos (\theta )}} ⇒Δθ>Ndcos(θ)λ通常来说,我们取 d = λ / 2 , θ = 0 d = λ/2, θ = 0 d=λ/2,θ=0 (boresight 方向,也就是雷达的中心朝向)。这时,角度分辨率公式为: θ R E S = 2 N {\theta _{RES}} = \frac{2}{N} θRES=N2
从上面的推导可以看出,角度分辨率主要依赖于两个因素: 1) 目标的方位角。在boresight方向分辨率最高。越靠近雷达FOV的边缘,角度分辨率越低。2)天线的个数。角度分辨率与天线个数城正比关系。第一个因素我们无法控制,而提高FMCW雷达角度分辨率的主要手段就是增加天线个数。
3.1.2 MIMO ( Multiple Input Multiple Output)技术
从角度分辨率的计算公式中可以看到,想要提高雷达的角度分辨率,必须增加接收天线的个数。但是,增加天线的个数,会使天线体积变得很大,此外每一个接收天线上都要附加一个单独的链路来处理信号,比如混频器、IF滤波器和ADC。不仅硬件设计变得复杂,而且成本也会增加。

采用MIMO (多发多收)的天线设计来降低接收天线的个数。比如,如果想要得到8个接收天线,采用2个发射天线和4个接收天线,这样就可以得到等效的8个虛拟接收天线阵列。一般来说,不同的发射天线会间隔发射,或者发射不同波形的信号,这样接收天线就可以区分来自不同发射天线的信号。
当发射天线有垂直方向的分布时,就可以测量目标的俯仰角度。下图就是一个典
型的3发4收的天线排列结构。等效的接收天线有12个,垂直方向上有两个天线
可以用来测量俯仰角度。

3.2 4D毫米波雷达发展趋势
3.2.1 芯片级联
4D成像雷达的核心在于较高的水平和垂直角度分辨率,这就需要增加发射和接收天线的个数。目前绝大多数毫米波雷达都是采用单片收发器,通常只有3发4收,也就是只有12个虛拟天线。一个增加虚拟天线的方案是基于现有的量产雷达,将多个雷达芯片进行级联,比如德国大陆的ARS540和华为的4D成像雷达。
ARS540采用4片级联的形式,将4片NXP的77GHz毫米波雷达收发器(MMIC)MR3003进行级联。每个MR3003是3发4收,4片联在一起就是12发16收,这样就可以产生192个虚拟天线。ARS540是第一个具备能够真正测量目标高度的毫米波雷达,其垂直角度分辨率可以达到2.3°,水平角度分辨率可以达到1.2°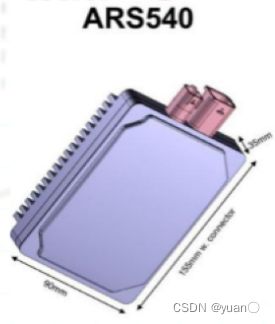
3.2.2 专用芯片
除了采用现有的量产雷达进行级联,还有的公司直接将多发多收的天线嵌入到一个雷达芯片里,比如Arbe, Vayyar 以及Mobileye。Arbe 提供的4D成像毫米波雷达Phoenix,采用48发48收,虚拟通道达到个2304个。Mobileye 同样也是48发48收的天线配置,水平和垂直角分辨率可以做到0.5°和2°。
3.2.3 标准芯片+软件提升
这种方案基于标准的雷达芯片,但是采用软件和AI的方法来提高雷达的分辨率。这里比较有代表性的是傲酷的虚拟孔径成像技术。传统FMCW雷达重复单一的发射波形,相位差来自于多根实体接收天线,而傲酷虚拟孔径成像雷达波形可以对发射波进行调频,调相、调幅,也就是说每根接收天线在不同时间产生不同的相位,形成“虚拟天线孔径”。而且这种调整是可以根据当前环境进行自适应的,也就是说根据上一帧的检测结果来调整当前帧的波形。
声明
本人所有文章仅作为自己的学习记录,若有侵权,联系立删。本系列文章主要参考了清华大学、北京理工大学、深蓝学院、百度Apollo等相关课程。
