常见图像算法总结 归一化 均值滤波 标准化 旋转

常见图像算法总结

1. 图像像素归一化

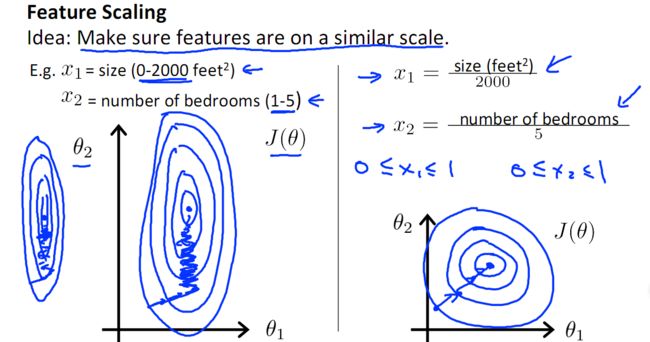
**图像的像素归一化是一个图像的预处理过程。**最常见的对图像预处理方法有两种，正常白化处理又叫图像标准化处理，另外一种叫归一化处理

众所周知图像是由像素组成的，灰度图是由单个像素矩阵组成的，而彩色图像是由三个矩阵所构成的，即我们常说的红，绿，蓝三通道。 每个像素矩阵的取值均是0-255之间的整数，虽然可以直接将原始图像的像素真实值直接作为神经网络模型的训练数据，但是这可能会给我们模型的训练过程带来一些问题，

原因：在深度神经网络(或其他算法)训练时一般使用较小的权重值来进行拟合，而当训练数据的值是较大整数值时，可能会减慢模型训练的过程。如果我们在将图像输入到神经网络之前对图像做像素值归一化的处理，即将像素值缩放到0-1之间，就能够避免很多不必要的麻烦。

方法(像素值归一化)：像素的归一化就是要把图片像素值数据经过某种算法限制在需要的一定范围内。归一化可以使没有可比性的数据变得具有可比性，同时保持相比较的数据之间的相对关系。

• L1归一化 : NORM_L1
• L2归一化 : NORM_L2
• INF归一化 : NORM_INF
• MINMAX归一化 : NORM_MINMAX(最常用）

(1) L1归一化:NORM_L1

L1归一化依据所有像素值之和，用原始像素值除以所有像素值之和即为原始像素值归一化后的值。
例如对于20.0,80.0,100.0三个像素值，它们的和为20.0+80.0+100.0=200.0。

所以20.0,80.0,100.0经过L1归一化后的值分别为0.1,0.4,0.5。

(2) L2归一化:NORM_L2

L2归一化依据于原始像素值组成的单位向量，用原始像素值除以所有原始像素值平方值之和的平方根即为原始像素值归一化后的值。

(3) INF归一化:NORM_INF

INF归一化依据于最大值，用原始像素值除以所有原始像素值中的最大值即为原始像素值归一化后的值。

(4)MINMAX归一化:NORM_MINMAX(最常用)

INF归一化依据于最大值与最小值的差值（记为delta），用原始像素值除以所有原始像素值中的最大值即为原始像素值归一化后的值。

在数据给定后 和 也可看做常数。就发现事实上就是对向量 按照比例压缩再进行平移 。所以归一化的本质就是一种线性变换。

(5) 好处

• 提升模型的收敛速度
• 提升模型的精度，让各个特征对结果做出的贡献相同。
• 深度学习中数据归一化可以防止模型梯度爆炸

注意：原图与归一化之后的运行结果完全一致，说明归一化不会改变图像本身的信息存储，但是通过打印出来的像素值可以发现，取值范围从0～255已经转化为0～1之间了，这个对于后续的神经网络或者卷积神经网络处理有很大的好处，tensorflow官方给出mnist数据集，全部采用了归一化之后的结果作为输入图像数据来演示神经网络与卷积神经网络。

2. 图像像素标准化

其中 和 代表样本的均值和标准差， 为最大值， 为最小值。标准化的本质就是一种线性变换。

• 归一化的缩放是“拍扁”统一到区间（仅由极值决定），而标准化的缩放是更加“弹性”和“动态”的，和整体样本的分布有很大的关系。
• 归一化：缩放仅仅跟最大、最小值的差别有关。
• 标准化：缩放和每个点都有关系，通过方差（variance）体现出来。与归一化对比，标准化中所有数据点都有贡献（通过均值和标准差造成影响）。
• 当数据较为集中时， 更小，于是数据在标准化后就会更加分散。如果数据本身分布很广，那么 较大，数据就会被集中到更小的范围内。
• 归一化： 输出范围在0-1之间 标准化：输出范围是负无穷到正无穷

3. 图像平移缩放旋转

3.1 平移

所以平移思路就是，将原先图像的横坐标和纵坐标分别加上一个数字，变成一个新的坐标，然后将原图中原坐标位置的RGB赋值给新图中新坐标。

image_shift.at<Vec3b>(counter1 + dx, counter2 + dy)[0] = image.at<Vec3b>(counter1, counter2)[0];
image_shift.at<Vec3b>(counter1 + dx, counter2 + dy)[1] = image.at<Vec3b>(counter1, counter2)[1];
image_shift.at<Vec3b>(counter1 + dx, counter2 + dy)[2] = image.at<Vec3b>(counter1, counter2)[2];

3.2 缩放

新图像的像素数是原图像n倍

	double mul_num = 0.8;//大于1是放大，小于1是缩小
	int row_num = (int)floor(image.rows * mul_num), col_num = (int)floor(image.cols * mul_num);
	Mat image_scale(row_num, col_num, CV_8UC3);
	for (int counter1 = 0; counter1 < row_num; counter1++)
	{
		for (int counter2 = 0; counter2 < col_num; counter2++)
		{
			//将筛孔缩小，对上画的大小
			int x = (int)1.0 / mul_num *counter1, y = (int)1.0 / mul_num *counter2;
			image_scale.at<Vec3b>(counter1, counter2 )[0] = image.at<Vec3b>(x, y)[0];
			image_scale.at<Vec3b>(counter1, counter2 )[1] = image.at<Vec3b>(x, y)[1];
			image_scale.at<Vec3b>(counter1, counter2 )[2] = image.at<Vec3b>(x, y)[2];
		}
	}
	//imshow("尺度变换", image_scale);
	imwrite("2.jpg", image_scale);//存储变换后的图像

3.3 旋转

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vZIgoCiT-1582982196787)(H:\笔记\算法总结.assets\image-20200229201426864.png)]

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main() {
	//读原图
	Mat image;

	image = imread("1.jpg", CV_LOAD_IMAGE_COLOR);

	if (!image.data)
	{
		cout << "找不到图片或无法打开图片\n";
		return -1;
	}
	//namedWindow("image_source", CV_WINDOW_AUTOSIZE);
	imshow("原图", image);
	double angle = 45 * 3.1415926 / 180.0;//把角度化成弧度
	int dis = ceil(sqrt(pow(image.rows, 2) + pow(image.cols, 2)));//新图像的长宽应该是原图像的对角线长度
	Mat image_nrota(dis, dis, CV_8UC3);
	float cenX = (image.rows+1) / 2 ,cenY = (image.cols+1) / 2 ;
	float a = dis / 2 - image.rows / 2;
	float b = dis / 2 - image.cols / 2;
	for (int counter1 = 0; counter1 < image.rows; counter1++)
	{
		for (int counter2 = 0; counter2 < image.cols; counter2++)
		{
			//计算应该平移的距离
			
			//按照仿射矩阵计算后进行平移
			int x = (counter1- cenX) * cos(angle) - (counter2-cenY) * sin(angle) + cenX+a,
				y = (counter1 - cenX) * sin(angle) + (counter2 - cenY) * cos(angle) + cenY+b;
			image_nrota.at<Vec3b>(x, y)[0] = image.at<Vec3b>(counter1, counter2)[0];
			image_nrota.at<Vec3b>(x, y)[1] = image.at<Vec3b>(counter1, counter2)[1];
			image_nrota.at<Vec3b>(x, y)[2] = image.at<Vec3b>(counter1, counter2)[2];

		}
	}
	imshow("旋转", image_nrota);
	imwrite("3.jpg", image_nrota);
	waitKey(0);
	system("pause");
	return 0;
}

3.4 图像处理：中值滤波&均值滤波

图像滤波，即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。

均值滤波和和中值滤波都可以起到平滑图像，虑去噪声的功能。

(1) 均值滤波

图片中一个方块区域（一般为3*3）内，中心点的像素为全部点像素值的平均值。均值滤波就是对于整张图片进行以上操作。

缺陷：均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。特别是椒盐噪声

(2) 中值滤波

在一连串数字｛1，4，6，8，9｝中，数字6就是这串数字的中值。由此我们可以应用到图像处理中。依然我们在图像中去3*3的矩阵，里面有9个像素点，我们将9个像素进行排序，最后将这个矩阵的中心点赋值为这九个像素的中值。

(5) 总结

1. 均值滤波和和中值滤波都可以起到平滑图像，虑去噪声的功能。

2. 均值滤波采用线性的方法，平均整个窗口范围内的像素值，均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。均值滤波对高斯噪声表现较好，对椒盐噪声表现较差。

3. 中值滤波采用非线性的方法，它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘，选择适当的点来替代污染点的值，所以处理效果好，对椒盐噪声表现较好，对高斯噪声表现较差。

波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。均值滤波对高斯噪声表现较好，对椒盐噪声表现较差。

3. 中值滤波采用非线性的方法，它在平滑脉冲噪声方面非常有效,同时它可以保护图像尖锐的边缘，选择适当的点来替代污染点的值，所以处理效果好，对椒盐噪声表现较好，对高斯噪声表现较差。