K-means算法和高斯混合模型的异同
写这篇文章的缘由是因为早上的机器学习讨论班大家对于一句话：用于向量化的k均值是高斯混合模型的一个硬版本（出处：机器学习导论，隐马尔科夫模型，p247，（15-36））产生了深刻的思考然后不理解，在结合老师的讲解以及搜索资料后，决定记录下来。
这一部分属于无监督学习的内容，无监督学习内容主要包括：Kmeans聚类算法、高斯混合模型GMM及EM算法等。
Kmeans聚类
其实聚类算法除了Kmeans，还有其它的聚类方式，记得曾经接触到的就有层次聚类、基于模糊等价关系的模糊聚类。Kmeans只不过是这些聚类算法中最为常见的一中，也是我用得最多的一种。Kmeans本身的复杂度也高（O(N^3)），因此Kmeans有很多其它的变种：
- 针对浮点型数据的运算，为提高运算效率，将浮点型Round成整形（我操作的话一般先乘一个系数，以使数据分布在整个整数空间，降低Round的数据损失）
- 层次化的Kmeans聚类(HIKM)
先给出一般Kmeans聚类问题的描述：
- 给定数据集:
- 将数据group成K个clusters
请注意：相对于监督学习算法，Kmeans虽然没有label信息，但聚类数K却是已知的，也就是说：使用Kmeans我们得计划好要聚成多少个cluster。
下面我们来总结一下 k-means 算法的具体步骤：
- 选定 K 个中心
的初值。这个过程通常是针对具体的问题有一些启发式的选取方法，或者大多数情况下采用随机选取的办法。因为前面说过 k-means 并不能保证全局最优，而是否能收敛到全局最优解其实和初值的选取有很大的关系，所以有时候我们会多次选取初值跑 k-means ，并取其中最好的一次结果。 - 将每个数据点归类到离它最近的那个中心点所代表的 cluster 中。
- 用公式
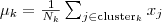计算出每个 cluster 的新的中心点。 - 重复第二步，一直到迭代了最大的步数或者前后的
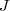的值相差小于一个阈值为止。
然后我们看一下周志华的机器学习这本书对k-means的定义。
所以我们要求的目标函数就是这个E函数。
高斯混合模型（GMM）
GMM 和 k-means 很像，不过 GMM 是学习出一些概率密度函数来（所以 GMM 除了用在 clustering 上之外，还经常被用于 density estimation ），简单地说，k-means 的结果是每个数据点被分配到其中某一个 cluster 了，而 GMM 则给出这些数据点被分配到每个 cluster 的概率，又称作 soft assignment，也称为软聚类 。
得出一个概率有很多好处，因为它的信息量比简单的一个结果要多，比如，我可以把这个概率转换为一个 score ，表示算法对自己得出的这个结果的把握。也许我可以对同一个任务，用多个方法得到结果，最后选取“把握”最大的那个结果；另一个很常见的方法是在诸如疾病诊断之类的场所，机器对于那些很容易分辨的情况（患病或者不患病的概率很高）可以自动区分，而对于那种很难分辨的情况，比如，49% 的概率患病，51% 的概率正常，如果仅仅简单地使用 50% 的阈值将患者诊断为“正常”的话，风险是非常大的，因此，在机器对自己的结果把握很小的情况下，会“拒绝发表评论”，而把这个任务留给有经验的医生去解决。
回想之前之前的高斯判别分析法（GDA），是通过计算样本的后验概率来进行判别，而后验概率是通过假设多元高斯模型来计算得来的。高斯模型的参数：均值、协方差，是由已标定（分类）的样本得来，所以可以看做是一种监督学习方法。
在GMM模型（属于无监督学习），给定未分类的m个样本（n维特征），假设可分为k个类，要求用GMM算法对其进行分类。如果我们知道每个类的高斯参数，则可以向GDA算法那样计算出后验概率进行判别。但遗憾的是，杨输入的样本未被标定，也就是说我们得不到高斯参数：均值、协方差。这就引出EM（Expectation Maximization Algorithm：期望最大化）算法。
EM算法的思想有点类似于k-means，就是通过迭代来得出最好的参数，有了这些参数就可以像GDA那样做分类了。GMM及EM具体步骤如下：
更通俗的，我们可以把高斯混合模型聚类算法EM步骤描述如下：
- 猜测有几个类别，既有几个高斯分布。
- 针对每一个高斯分布，随机给其均值和方差进行赋值。
- 针对每一个样本，计算其在各个高斯分布下的概率。
注：当高斯混合模型的特征值维数大于一维时，在计算加权的时候还要计算协方差，即要考虑不同维度之间的相互关联。
上面这个图可以理解为，一开始给的小球都是不知道它的颜色的，在经过多次的迭代，改变期望和方差后，同类颜色的小球的正态分布函数曲线逐渐趋向稳定，这样也就形成了各个不同的类。当然上述给出的只是一维的例子，其他的高维可以以此类推。
经过上述的介绍，我觉得已经可以理解提出的那句话的意思了。（用于向量化的k均值是高斯混合模型的一个硬版本）
1.GMM和K-means很相似，相似点在于两者的分类受初始值影响；两者可能限于局部最优解；两者类别的个数都要靠猜测。
2.K-means属于硬聚类，要么属于这类，要么属于那类，而GMM属于混合式软聚类，一个样本70%属于A，30%属于B；同时多维的GMM在计算均值和方差时使用了协方差，应用了不同维度之间的相互约束关系。
3.从欧式距离和马氏距离来说，见下图K-means和GMM的优化函数
K-means是欧式距离，而GMM是马氏距离，当协方差非对角线元素为0时，马氏距离也就变成了欧式距离。
附上：欧式距离，马氏距离介绍
Reference ：
https://blog.csdn.net/Kevin_cc98/article/details/73742037
https://blog.csdn.net/xiahouzuoxin/article/details/45747653
http://blog.sina.com.cn/s/blog_1584387c90102x0c9.html
https://blog.csdn.net/hujingshuang/article/details/46564237
https://blog.csdn.net/jyl1999xxxx/article/details/53734088?locationNum=12&fps=1
机器学习，周志华