apriori数据集_Apriori算法详解
Apriori算法简介
Apriori算法是一种常用的用于挖掘出数据关联规则(Association Rules)的算法,“apriori”在拉丁语中翻译为“来自以前”,顾名思义,这个算法是使用先验知识来预测数据的关联规则。
说到关联规则,我们不得不提到一个经典案例——啤酒与尿布。在这个案例中,沃尔玛发现看似两个无关的商品,它们却经常被一起购买,这是为什么呢?在美国有婴儿的家庭中,一般是母亲在家中照看婴儿,年轻的父亲前去超市购买尿布,父亲在购买尿布的同时,往往会顺便为自己购买啤酒,这样就会出现啤酒与尿布这两件看上去不相干的商品经常会出现在同一个购物篮的现象。这两种看似不相干的商品之间显现出强相关性,于是商家可以将啤酒货架放在尿布货架旁边以增加收益。
这个案例中研究啤酒与尿布的关系的方法就叫做“购物篮分析”,本质上就是挖掘数据关联规则,而Apriori算法就是最经典的关联规则挖掘算法。
相关概念
支持度(Support)
数据集中包含该项集的数据所占数据集的比例,度量一个集合在原始数据中出现的频率。关联规则A->B的支持度support=P(AB),指的是事件A和事件B同时发生的概率(相当于联合概率)。
通常我们需要事先设置一个支持度的阈值来对项集进行筛选。
置信度(Confidence)
置信度 ,指的是发生事件A的基础上发生事件B的概率(相当于条件概率)。
频繁k项集(Frequent k Itemset)
项集就是项的集合,比如牛奶和面包组成一个集合{牛奶,面包},那么牛奶和面包就是项,而{牛奶,面包}为一个二项集。频繁项集表示的就是在数据集中频繁出现的项集。如果事件A中包含k个元素,那么称这个事件A为k项集,并且事件A满足最小支持度阈值的事件称为频繁k项集。
Apriori算法原理
Apriori算法性质
如果某个项集是频繁的,那么它的所有子集也是频繁的;
如果某个项集是非频繁的,那么它的所有超集也是非频繁的;
如果频繁k项集集合中包含单个项目i的个数小于k-1,则i不可能在频繁k项集中;
基于此,Apriori算法从单元素项集开始,通过组合满足最小支持度的项集来形成更大的集合。
其实Apriori算法就是通过排除法来选择频繁项集和关联规则,算法的目标是找到最大的频繁k项集。
Apriori算法过程
Apriori算法过程分为两个步骤:
通过迭代,检索出事务数据库中的所有频繁项集,即支持度不低于用户设定的阈值的项集;
利用频繁项集构造出满足用户最小置信度的关联规则。
具体过程就是:
先搜索出候选1项集并计算对应的支持度,通过筛选去掉支持度低于阈值的候选1项集,得到频繁1项集;
通过连接频繁1项集得到候选2项集并计算对应的支持度,通过筛选去掉支持度低于阈值的候选2项集,得到频繁2项集;
以此类推,不断循环,直到无法发现频繁k+1项集为止,此时的频繁k项集便是算法的输出结果。
由频繁项集产生强关联规则
在找到所有频繁项集后,我们还需要根据频繁项集生成关联规则:
对于每个频繁项集L,生成其所有的非空子集;
对与L的每个非空子集x,计算其置信度confidence(x),若confidence(x)大于等于最小置信度,则强规则x->(L-x)成立。
R语言中实现Apriori算法
R语言中的Apriori算法实现包含在arules包中。
数据源
利用arules包中自带的Groceries数据集,该数据集是来自一个现实世界中的超市经营一个月的购物数据,包含了9835次交易。
> library(arules)
> data(Groceries)
> Groceries
transactions in sparse format with
9835 transactions (rows) and
169 items (columns)
探索性数据分析
通过inspect()函数可以看到超市的交易记录。
> inspect(Groceries[1:5])
items
[1] {citrus fruit, semi-finished bread, margarine, ready soups}
[2] {tropical fruit, yogurt,
coffee}
[3] {whole milk}
[4] {pip fruit, yogurt, cream cheese, meat spreads}
[5] {other vegetables, whole milk, condensed milk, long life bakery product}
通过summary()函数可以查看该数据集的一些基本信息。
> summary(Groceries)
transactions as itemMatrix in sparse format with
9835 rows (elements/itemsets/transactions) and
169 columns (items) and a density of 0.02609146
most frequent items:
whole milk other vegetables rolls/buns soda
2513 1903 1809 1715
yogurt (Other)
1372 34055
element (itemset/transaction) length distribution:
sizes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2159 1643 1299 1005 855 645 545 438 350 246 182 117 78 77 55 46
17 18 19 20 21 22 23 24 26 27 28 29 32
29 14 14 9 11 4 6 1 1 1 1 3 1
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 2.000 3.000 4.409 6.000 32.000
includes extended item information - examples:
labels level2 level1
1 frankfurter sausage meat and sausage
2 sausage sausage meat and sausage
3 liver loaf sausage meat and sausage
通过itemFrequency()函数可以查看商品的交易比例。
> itemFrequency(Groceries[,1:3])
frankfurter sausage liver loaf
0.058973055 0.093950178 0.005083884
通过以上数据我们可以得出以下结果:
该数据集一共有9835行(交易记录),169列(所有交易的商品种类),因此矩阵中共有 个位置,我们可以得出,在30天内共有 件商品被购买,进一步可以得出在每次交易中包含了 件商品被购买
most frequent items:列出了事务型数据中最常购买的商品。whole milk在9835次交易中被购买了2513次,因此我们可以得出结论:whole milk有2513/9835=25.6%的概率出现在所有的交易中;
element (itemset/transaction) length distribution:呈现了一组关于交易规模的统计,总共有2159次交易中包含一件商品,有1次交易中包含了32件商品。我们可以看出,25%的交易中包含了两件或者更少的商品,大约一半的交易中商品数量不超过3件。
为了直观地呈现统计数据,可以使用itemFrequenctyPlot()函数生成一个用于描绘所包含的特定商品的交易比例的柱状图。因为包含很多种商品,不可能同时展现出来,因此可以通过support或者topN参数进行排除一部分商品进行展示。
> itemFrequencyPlot(Groceries,support = 0.1) # support = 0.1 表示支持度至少为0.1
> itemFrequencyPlot(Groceries,topN = 20) # topN = 20 表示支持度排在前20的商品
通过使用image()函数可以可视化整个稀疏矩阵。
> image(Groceries[1:5]) # 生成一个5行169列的矩阵,矩阵中填充有黑色的单元表示在此次交易(行)中,该商品(列)被购买了
从上图可以看出,第一行记录(交易)包含了四种商品(黑色的方块),这种可视化的图是用于数据探索的一种很有用的工具。它可能有助于识别潜在的数据问题,比如:由于列表示的是商品名称,如果列从上往下一直被填充表明这个商品在每一次交易中都被购买了;另一方面,图中的模式可能有助于揭示交易或者商品的有趣部分,特别是当数据以有趣的方式排序后,比如,如果交易按照日期进行排序,那么黑色方块图案可能会揭示人们购买商品的数量或者类型受季节性的影响。这种可视化对于超大型的交易数据集是没有意义的,因为单元太小会很难发现有趣的模式。
训练模型
> grocery_rules 运行apriori()函数很简单,但是找到支持度和置信度参数来产生合理数量的关联规则时,可能需要进行大量的试验与误差评估。
如果参数设置过高,那么结果可能是没有规则或者规则过于普通而不是非常有用的规则;如果阈值太低,可能会导致规则数量很多,甚至需要运行很长的时间或者在学习阶段耗尽内存。
aprior()函数默认设置 和 。
> apriori(Groceries)
set of 0 rules
因为 ,则意味着该商品必须至少出现在 次交易中,在前面的分析中,我们发现只有8种商品的 ,因此使用默认的设置没有产生任何规则也不足为奇。
解决支持度设定问题的一种方法是:考虑一个有趣的模式之前,事先想好需要的最小交易数量,例如:我们可以认为如果一种商品一天被购买了2次,一个月也就是60次交易记录,这或许是我们所感兴趣的,据此,可以计算所需要的支持度 ;
关于置信度:设置太低,可能会被大量不可靠的规则淹没,设置过高,可能会出现很多显而易见的规则致使我们不能发现有趣的模式;一个合适的置信度水平的选取,取决于我们的分析目标,我们可以尝试以一个保守的值开始,如果发现没有具有可行性的规则,可以降低置信度以拓宽规则的搜索范围。
在此例中,我们将从置信度0.25开始,这意味着为了将规则包含在结果中,此时规则的正确率至少为25%,这将排除最不可靠的规则。
表示规则中至少包含两种商品,这可以防止仅仅是由于某种商品被频繁购买而创建的无用规则,比如在上面的分析中,我们发现whole milk出现的概率(支持度)为25.6%,很可能出现如下规则: ,这种规则是没有意义的。
最终,根据上面的分析我们确定如下参数设置:
> grocery_rules 0.006,confidence = 0.25,minlen = 2))
> grocery_rules
set of 463 rules
关联规则可视化
使用arulesViz包可对关联规则进行可视化。
> library(arulesViz)
通过plot()函数可以得到生成规则的散点图以及散点矩阵
> plot(grocery_rules)
> plot(grocery_rules@quality)
> highLiftRules "lift"), 5)
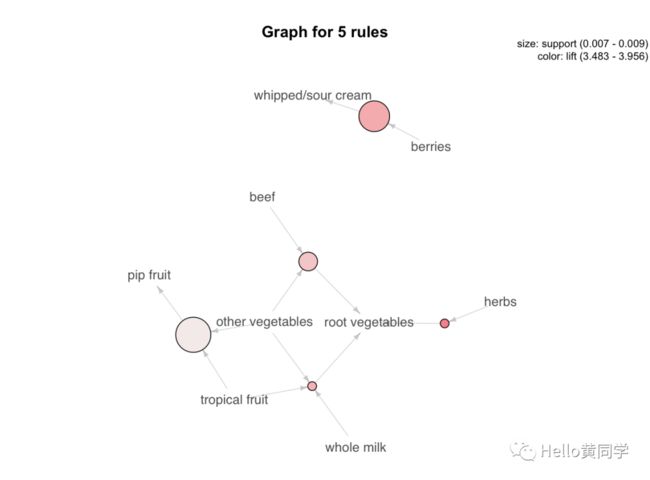
> plot(highLiftRules, method = "graph", control = list(type = "items"))
圆圈的大小表示支持度的大小,不同的项目通过有向箭头指向同一个支持度,表示相应项目组成的一个项集。
评估模型的性能
> summary(grocery_rules)
set of 463 rules
rule length distribution (lhs + rhs):sizes # 前件+后件的规则长度分布
2 3 4
150 297 16 #有150个规则只包含2种商品,297个规则包含3种商品,16个规则包含4种商品
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 2.000 3.000 2.711 3.000 4.000
summary of quality measures:
support confidence coverage lift
Min. :0.006101 Min. :0.2500 Min. :0.009964 Min. :0.9932
1st Qu.:0.007117 1st Qu.:0.2971 1st Qu.:0.018709 1st Qu.:1.6229
Median :0.008744 Median :0.3554 Median :0.024809 Median :1.9332
Mean :0.011539 Mean :0.3786 Mean :0.032608 Mean :2.0351
3rd Qu.:0.012303 3rd Qu.:0.4495 3rd Qu.:0.035892 3rd Qu.:2.3565
Max. :0.074835 Max. :0.6600 Max. :0.255516 Max. :3.9565
count
Min. : 60.0
1st Qu.: 70.0
Median : 86.0
Mean :113.5
3rd Qu.:121.0
Max. :736.0
mining info:
data ntransactions support confidence
Groceries 9835 0.006 0.25
> inspect(grocery_rules[1:5])
lhs rhs support confidence coverage lift
[1] {pot plants} => {whole milk} 0.006914082 0.4000000 0.01728521 1.565460
[2] {pasta} => {whole milk} 0.006100661 0.4054054 0.01504830 1.586614
[3] {herbs} => {root vegetables} 0.007015760 0.4312500 0.01626843 3.956477
[4] {herbs} => {other vegetables} 0.007727504 0.4750000 0.01626843 2.454874
[5] {herbs} => {whole milk} 0.007727504 0.4750000 0.01626843 1.858983
count
[1] 68
[2] 60
[3] 69
[4] 76
[5] 76
这里需要解释一下lift(提升度),表示用来度量一类商品相对于它的一般购买率,此时被购买的可能性有多大。通俗的讲就是:比如第一条规则 , 表明购买pot plants之后再购买whole milk商品的可能性是没有购买pot plants但是购买了whole milk的可能性的1.565倍;
第一条规则解读:如果一个顾客购买了pot plants,那么他还会购买whole milk,支持度support为0.0070,置信度confidence为0.4000,我们可以确定该规则涵盖了大约0.7%的交易,而且在购买了pot plants后,他购买whole milk的概率为40%,提升度lift值为1.565,表明他相对于一般没有购买pot plant商品的顾客购买whole milk商品的概率提升了1.565倍,我们在上面的分析中知道,有25.6%的顾客购买了whole milk,因此计算提升度为 ,这与显示的结果是一致的,注意:标有support的列表示规则的支持度,而不是前件(lhs)或者后件(rhs)的支持度。
提升度 , 与 是相同的。
如果 ,说明这两类商品在一起购买比只有一类商品被购买更常见。一个大的提升度值是一个重要的指标,它表明一个规则是很重要的,并反映了商品之间的真实联系。
提高模型的性能
对关联规则集合排序:根据购物篮分析的目标,最有用的规则或许是那些具有高支持度、信度和提升度的规则。arules包中包含一个sort()函数,通过指定参数by为"support","confidence"或者"lift"对规则列表进行重新排序。在默认的情况下,排序是降序排列,可以指定参数decreasing=FALSE反转排序方式。
> inspect(sort(grocery_rules,by="lift")[1:10])
lhs rhs support confidence lift
3 {herbs} => {root vegetables} 0.007015760 0.4312500 3.956477
57 {berries} => {whipped/sour cream} 0.009049314 0.2721713 3.796886
450 {tropical fruit,other vegetables,whole milk} => {root vegetables} 0.007015760 0.4107143 3.768074
174 {beef,other vegetables} => {root vegetables} 0.007930859 0.4020619 3.688692
285 {tropical fruit,other vegetables} => {pip fruit} 0.009456024 0.2634561 3.482649
176 {beef,whole milk} => {root vegetables} 0.008032537 0.3779904 3.467851
284 {pip fruit,other vegetables} => {tropical fruit} 0.009456024 0.3618677 3.448613
282 {pip fruit,yogurt} => {tropical fruit} 0.006405694 0.3559322 3.392048
319 {citrus fruit,other vegetables} => {root vegetables} 0.010371124 0.3591549 3.295045
455 {other vegetables,whole milk,yogurt} => {tropical fruit} 0.007625826 0.3424658 3.263712
提取关联规则的子集:可以通过subset()函数提取我们感兴趣的规则。
> fruit_rules in% "pip fruit") # items 表明与出现在规则的任何位置的项进行匹配,为了将子集限制到匹配只发生在左侧或者右侧位置上,可以使用lhs或者rhs代替
> fruit_rules
set of 21 rules
> inspect(fruit_rules[1:5])
lhs rhs support confidence lift
127 {pip fruit} => {tropical fruit} 0.020437214 0.2701613 2.574648
128 {pip fruit} => {other vegetables} 0.026131164 0.3454301 1.785237
129 {pip fruit} => {whole milk} 0.030096594 0.3978495 1.557043
281 {tropical fruit,pip fruit} => {yogurt} 0.006405694 0.3134328 2.246802
282 {pip fruit,yogurt} => {tropical fruit} 0.006405694 0.3559322 3.392048
Apriori算法的缺点与改进
从以上的算法执行过程可以看到Apriori算法的缺点:
在每一步产生侯选项集时循环产生的组合过多,没有排除不应该参与组合的元素(空间、时间);
每次计算项集的支持度时,都对全部记录进行了一遍扫描比较,如果是一个大型的数据库的话,这种扫描比较会大大增加计算机系统的I/O开销。而这种代价是随着数据库的记录的增加呈现出几何级数的增加(时间)。
主要考虑从三个方面优化:
数据库的压缩,如果一个条目(或者说项目)不包含任何一个k项集,那么它不可能包含任何一个k+1项集,即在下一次的遍历数据库时,不需要再去对该条目进行检查(通常做法是删除该条目,或者将这个条目做上标记)。
缩小候选项集的个数,即动态项集计数。在某个条目的统计之后,如果发现某个候选项集的计数已经满足了最小支持度,那么可以将这个项集直接放入到频繁项集中,这样以后就不用对该项集进行计数了
在连接的步骤之前,先利用之前提到的Apriori算法的第三个性质对项集进行筛选,提前删除不满足的项集。对k-1项项集中的每一个元素进行计数,若某个元素的个数小于k-1,则将k-1项集中包含该元素的项集删除。这样可以极大的减小了可能产生的候选项集的数量。