梯度消失/爆炸与RNN家族的介绍(LSTM GRU B-RNN Multi-RNNs)-基于cs224n的最全总结

vanishing gradients and fancy RNNs（RNN家族与梯度消失）

内容大纲：

Vanishing gradient

首先我们需要建立一个直觉，如果网络结构如下

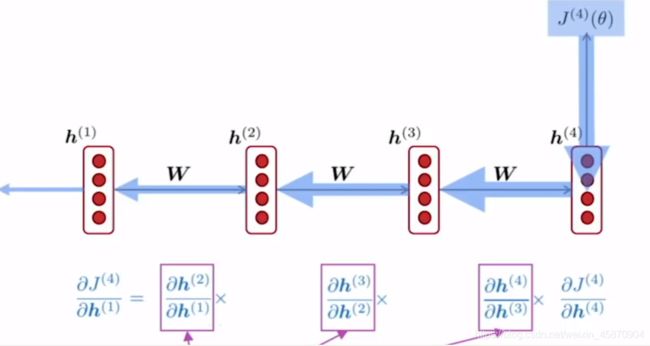
反向传播基于链式法则依次计算每一个step t的梯度或者说导数。注意，它们都是通过乘积形式连接的。

所以，如果，当倒数第一步计算出的梯度很小的时候，随着反向传播和链式法则计算的不断进行，这个梯度会越来越小，最终导致整个梯度下降的优化难以进行下去。

一个更加正式的定义（或者说一个数学证明过程）（比较抽象，可以定性理解）：

可以看到，链式法则的结果里面有一个Wh，如果Wh的值非常小，那么它再不断与自己相乘的话，整个的梯度就会变得很小很小。

这里还用两边同取L2范数做了证明，因为sigmoid函数的特性，我们的边界时1，所以一篇论文写道如果Wh矩阵的最大特征值都小于1，那么整个梯度会下降的非常快，而如果最大特征值大于1，那么梯度经过一层层传播会变得非常大，称之为梯度爆炸。

为什么我们需要考虑整个问题？

如果梯度是vanishing的，那么对于梯度信号来说，其就很可能只受到其附近的梯度信号的影响，而省略掉了远处的信息，这是有悖于我们的初衷的，当然从语言学的角度来看，这就意味着整个训练可能是失败的。

从理论上来说，另一种解释是梯度可以被看做过去对于未来施加影响的方法。-很多时候，机器学习都是一种直觉和定性的思考和分析

如果说gradient很小，那么就可能说明了两个问题：

1. step t and t+n的data可能是没有什么dependency的
2. 或者我们可能使用了错误的参数去捕捉step t and t+n data 的 dependency

而在实际情况下，其实我们往往难以去分辨到底发生了两种情况中的哪一种。

下面来几个具体的栗子：

上面就是一个有趣的栗子，对于我们来说，很明显应该填门票，因为前面大量出现了这个单词，且整个语境也是这个逻辑，但对于机器来说,RNN模型表现的可能很差，因为要想成功预测出tickets，其需要学习第7 个 step的 tickets和目标 tickets的依赖，但如果梯度很小，那么这种前后上下文信息依赖其很可能就会没有学习到或者说丢失，那么这里的预测就很可能是失败的。

这个栗子更为经典，因为这也是我们在初学英语时最容易犯的一个错误，这个地方是填is 还是 are？当然是is，因为我们明白这句话的语法结构来看，在依赖树上，__应该是与writer相连的，但RNN却很容易填成are，这就是由于gradient vanishing的问题所导致的，对于其来说，最近的单词的梯度信号更强，所以其很容易犯错，也存在很多paper提出了其的这一点问题。

Exploding gradient

为什么梯度爆炸是一个问题？

大家注意不要把梯度爆炸和vanishing和学习率过大和过小搞混了···。学习率是步长，梯度是direction-方向向量的下降最快方向特殊版。

灵魂可视化，大家就明白了

如果出现这种情况，你可能只能回到上一个check point.

如何解决呢？答案是梯度裁剪（gradient clipping），当然我相信我在另外一篇博客中吴恩达老师也讲到过这个问题，那时候好像说的是合理的随机初始化W的方法，大家可以看看我的另外一篇博客，当然不止这种办法。梯度裁剪和梯度爆炸有不同的解决方案。

来一张官方教材的可视化图-当优化碰到了悬崖

criterion（标准）

插一个动量梯度下降的简单解释，当你在一个方向上已经走了很多步后，你可以在下一步迈出更大的一步，而如果你改变了方向，那么你应该迈出较小的一步，这是一种动量积累的思想，也是一种审时度势、审慎的态度。这种梯度裁剪与正则化有什么联系呢？这值得进一步研究。一个角度是如何更好的最优化，一个角度是如何更好防止模型的过拟合，过度依赖训练数据。

如何修复vanishing gradient的问题

在传统的RNN中，一直含有前面的信息（原文用的是preserve这个词）在很多timesteps后是非常困难的。

对于经典的vanilla RNN，隐藏状态一直是在重写下面这个数学公式

$$h(t)=\sigma (W_h{h}^{(t-1)}+W_x{X}^{(t)}+b)--线性变换+偏置+非线性变换$$

那么，如果我们能够有一个含有separate memory的RNN呢？

我们需要一些单独的地方去存储我们需要的信息。 -所以LSTM Long short-Term Memory RNNs.

LSTM（Long short-Term Memory）

LSTM的基本思想概述：

1. 不同于传统的RNN，是拥有hidden state h(t) 和 cell state c(t)

   1. 两个都是长度为n的向量
   2. cell像计算机的内存一样，存储一些长期项的信息
   3. LSTM可以删除，写入和阅读信息从cell中（英语看多了喜欢倒装）

2. 选择删除/写入/阅读都是由一个gates controlled的

   1. gates也是一个长度为n的向量-其与隐藏层长度一致
   2. 每一个timestep，门元素可以为open（1），closed（0)，或者位于两者中间-大意是1代表信息通过门，0代表信息被隔离在外，不能通过该门
   3. 门是动态的，其值的计算是会基于当前上下文来进行改变的。
      

LSTM的细节：

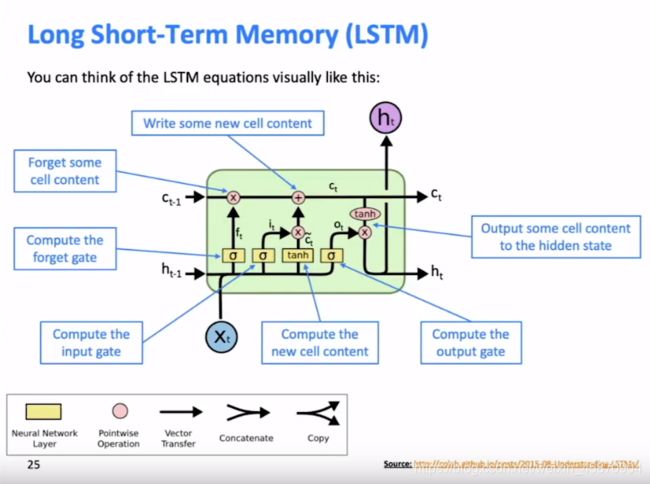
三个门和cell组成，主要细节如下面的PPT所示，我来进行一个简单的翻译总结。

1. forget gate 控制的是当前cell state是否需要接受前一个cell state的信息

2. input gate 控制的是new cell state content的哪一部分需要被输入cell

3. output gate 控制的是cell的哪一部分应该被输出到隐藏层状态-因为实际上cell相当于内存，而隐藏层状态是会随着网络传播的，所以我们称之为output.

   可以看到，门的三个状态都是由sigmoid作为激活函数的，所以门向量每一个元素的值被控制到0~1.

下面的三个cell state的具体计算我就不翻译了，大家看看即可，反正大概就是将门函数应用到具体的当前信息的传播选择中。

注意的是，门函数在cell状态的选择中的应用是利用逐元素相乘-（element-wise product）

tanh函数：

网络的总体图形化结构

具体的中间部门结构的可视化图像：-非常好理解

最后的c(t)在进入hidden state前为什么需要通过tanh进行映射变换，我想有两种可能性，第一个是如果你想要做一个非线性变换，存在梯度可以学习的话，加tanh函数是一个不错的选择，第二tanh可以将值控制到（-1到1），这可以使得其与o（t）的element-wise product的值在一个可控范围内，我相信这可能对于hidden state这个长度为n的向量来说是有益的。当然我认为做一个非线性变换更加合理，因为线性变换其实难以学到实质性的内容,神经网络的强大学习能力就是由许多非线性变换组合而成的。

还有一位现场上课的同学提出的问题很有意思，他说为什么f(t)是经过前一个隐藏层状态和输入计算而来，而不是基于前一个cell state-某个东西，也就是f(t)的定义没有体现任何关于c(t-1)的信息，但是实际上，h(t-1)很有可能包含有c(t-1)的输出，如果其都没有c(t-1)的输出，那么说明c(t-1)可能也没有意义，所以实际上h(t-1)是有上一个cell state的信息的，并不是完全没有任何联系的。

这说明深度学习的创造很多时候是依靠直觉的，很多东西都缺少严格的数学公式证明和解释性。

大概总结一下一些RNN维度的问题-可依次调换两个维度的顺序，但后面要跟着改：

1. word vector-one hot encoding((1,V)) V语料库大小

2. word to vector (1,d) d维稠密向量

3. We(d,n)

4. h(···) (1,n) --大家可能会问：最后softmax计算之前应该向量的维度又回到了语料库的长度才对，这要看

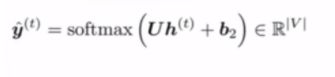
   U矩阵的维度定义如何了，按理来说应该是(n,v),还有可能不这样对应，而以索引的方式存储（例如Bert预训练好的分词和word2vector都是索引对应的)，后面有时间再回顾–手动测试看看代码吧。

5. c(····) (1,n)

6. 三个门向量(全部为(1,n))

7. Wh(n,n)

   实际上，这个d应该就是n，只是定义的符号不同而已。

   We和Wn的维度应该是相同的，同时，他们在整个神经网络中也是同一个矩阵。
   一个重要的点是hidden state的size其实是我们去定义的，我们想要多大的一个表示，所以或许可以称其为一个超参数

LSTM是如何解决vanishing gradients的问题的？

相信大家经过前面的概述，应该已经大概明白了相关的道理.

实际上，LSTM最大的提升就是其可以使得RNN更加容易去保存前面的信息即使经过了很多timesteps

1. 例如你可以将forget gate设置为每一次都完全记住前面的cell state的信息，这样info会被无限期的保留
2. 作为对比，对于一般的vanilla RNN来说，想要去学习一个recurrent weight matrix Wh去一直保存信息在hidden state是非常困难的
3. 但是值得注意的是，LSTM并不能保证完全解决了vanishing/exploding gradient (主要是vanishing)的问题，只是提供一个更加容易的方法去学习一种长距离的dependencies.

LSTM最重要的就是提供了一个记忆单元，其可以存储信息并且可以提供一条shortcut，给hidden state加上一些前面消失了但本不应该消失的信息的梯度，从而使得整个神经网络或者说RNN具有记忆性。

计算梯度的时候，还是需要用到多变量链式法则，即求和，当然我们是直接使用pytorch，所以并不需要我们自己去计算。

LSTM发展很快，但这些年transformer渐渐替代了LSTM成为了更加主流的方法;

GRU(Gated recurrent units)-两个门解决了问题

GRU的出现事实上是为了简化LSTM繁琐的计算步骤，其基本思想也是通过记忆和存储长期的信息来抵消vanishing gradient带来的问题，也就是拓展神经网络的记忆性。例如，如果update gate被设置为0，那么hidden state就会一直保持不变，当然，这不是一个好的选择，但这体现了其可以实现一定的信息存储或者说记忆功能。

可以看到最后的h(t)采用的是一种平衡参数法，加起来等于1的两个系数，这种思想非常常用。

LSTM VS GRU

LSTM和GRU并没有明显的实验证据表明两者的效果谁更好

但一般来说如果你追求效率和速度，选择GRU

如果你有很多training data，你可以选择LSTM，因为其有更多的参数需要数据去训练和学习

vanishing gradient和 exploding gradient当然不仅仅只是RNN的问题，在许多深层神经网络中都存在这个问题，只要层数L很深，那么输出的前一层的值都可能算出来是很大或者很小的，那么如果其算出来的梯度很大，随着反向传播，梯度呈指数级增加，就会出现gradient exploding的问题，而如果其算出来很小，（小于1比较多），随着层数的加深，梯度会越来越小越来越小，导致整个优化难以进行。

例如，研究人员发现，很多深层神经网络有时候甚至会表现得不如浅层神经网络，这就是因为其难以学习，而加入shortcut connection时，他们发现这种问题得到了有效的解决。

那么如何解决这种问题呢？

1. 一个典型有效的方法是加入一个short connection，例如resnet的网络架构

2. 或者中间插入些Dense net 全连接层-研究证明dense net效果很好

3. Highway connections，基于LSTM提出

   设置一个动态门来控制是经过transformation layer还是 identity connection（直连）

小结：

所以vanishing/exploding gradients是一个general的问题，RNN又是尤其严重的因为其重复×一个相同的weight matrix Wh，详情可以研究论文。

Bidirectional RNNs 双向RNN-概念简单

概念的引入，为什么我们需要双向RNN，动力是什么？
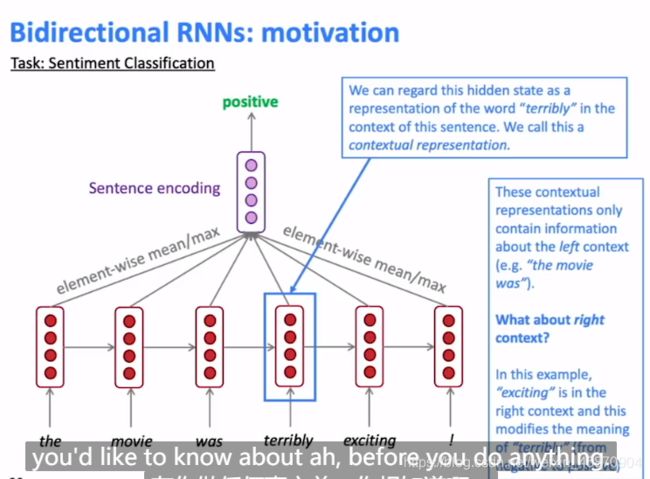
看一看下面这个情绪分类的例子：

hidden state一直到terribly这里一直都是表现的是负向情绪，而整个句子的关键恰恰是最后的exciting和！，它们决定了整个句子是postive的，所以我们需要RNN来平等地对待left and right infomation，就像我们过马路要左右两边都看看一样。

​

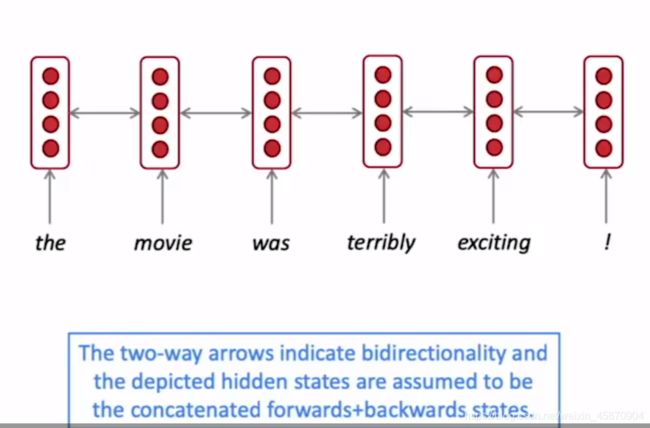
双向RNN的结构，先双向同时编码，最后整合-concatenated（注意的是，不同方向应用的是不同的权重矩阵）-相同的会怎么样？

大家可以自己思考思考-抽象思考非常重要。-有一些论文它们使用的是同样的权重，如果你有同样的训练数据，可以做一些尝试，经常想思考题十分重要。

一般来说，是同时训练双向网络的。

一个更为简易的图解网络：

事实上，并不是所有任务RNN都会表现的更好，例如LM-语言建模，你只能依赖左边的文本输入。

所以RNN适用的是输入是整个文本序列，例如文本情绪识别，对于这种输入，其表现是非常强大的。-这使得学习上下文变得更加容易。

目前最火的NLP预训练模型（Bidrectional encoder representations from transformers）就包括这种思想。

Multi-layer RNNS

我们首先需要建立一个直觉-RNN总是擅长很深刻的去捕捉一个维度的特征，例如可能是句义可能是语法结构，但是我们如果想要让其更加强大，我们就可以建立多个RNN进行堆叠(stacked RNNs)，分别去计算不同的特征，最终变得非常的powerful。

multi-layer RNNs

RNN layer i的hidden state是RNN layer i+1的输入-计算顺序一般来说有两种，一种是先全部计算RNN layer 1 ，一种是计算the这个单词的一列全部，但是对于双向RNN，我们就不具有这种灵活性了，我们只能选择一层一层的计算。

RNN只能顺序计算，不能并行计算，这也是一个其不能变得很深的原因。-下面PPT有目前的一些实例的介绍，关于多层RNN到底有多少层。skip-connections和dense-connections都是非常重要的使其变深更加有效学习的tricks。

这篇博文以及这堂课的总结-一些实用的技巧：

1. LSTM
2. 梯度裁剪
3. 双向RNN
4. multi-layer RNN