Domain Agnostic Learning with Disentangled Representations

Domain Agnostic Learning with Disentangled Representations

第一章 领域未知的表示学习

---

---

前言

Domain Agnostic Learning with Disentangled Representations 为ICML2019的论文，主要用接纠缠解决domain agnostic。 没看之前，以为是一个multi-source to single-target.
论文是single-source 去预测 multi-target。而且在训练过程中，使用到了target数据，其实是一个领域自适应问题，不是zero-shot的问题。

这篇论文的主要流程。

---

一、方法介绍和相关代码

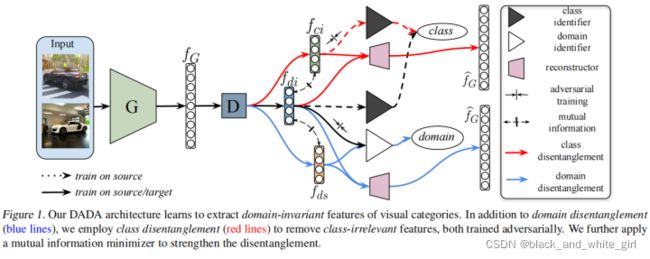
本文使用了解纠的方法，首先分解了domain feature 为domain-special 和 domain-invariant，关于domain的解纠缠使用了互信息和对抗反梯度domain分类。

然后基于domain-invariant的特征进行语义分类，然后语义分类结果的对抗，获取了无关语义的特征提取器。其中使用了domain-invariant 和 class-inrariant的互信息，让两种特征尽量不相关，最后保留了domain-invariant-class-special feature进行分类。

其中还使用了reconstruction的方法，希望能还原以前的数据，这样的方法一般可以用在监督学习中，供下游任务进行分类使用。。

二、解纠缠代码

首先论文先用generate 生成了F1这样的base feature，然后利用三个神经网络进行解纠缠：

 self.C = nn.ModuleDict({
            'ds': Classifier(source=source, target=target),   ## domain-special
            'di': Classifier(source=source, target=target),   ## domain-inviriant
            'ci': Classifier(source=source, target=target)    ## class-inviriant
        })  

其实是一个神经网络映射到三个空间，接下来三个空间分别进入不同的分类器和loss进行约束。

2.1 约束1

交叉熵，对三个解纠缠的特征都进行了分类。

  for key in ['ds', 'di', 'ci']:
      _loss['class_src_' + key] = self.xent_loss(   self.C[key](self.D[key](feat_src)), label_src)
      
 _sum_loss = sum([l for _, l in _loss.items()])
 _sum_loss.backward()

---

约束2

提示：这里对文章进行总结：

  _loss['ds_src'] = self.xent_loss(self.C['ds'](self.D['ds'](self.G(img_src))), label_src)
   _loss['di_src'] = self.xent_loss(self.C['di'](self.D['di'](self.G(img_src))), label_src)
 

# on target domain
_loss['discrepancy_ds_di_trg'] = _discrepancy(self.C['ds'](self.D['ds'](self.G(img_trg))), self.C['di'](self.D['di'](self.G(img_trg))))

约束3

本文insight 比较优秀的地方, 提取class-domain-invariant
减少(ds, ci) and (di, ci)的互信息学。

区分domain-special 和 domain-invaviant

 for i in range(0, self.mi_k):
            ds_src, ds_trg = self.D['ds'](self.G(img_src)), self.D['ds'](self.G(img_trg))
            di_src, di_trg = self.D['di'](self.G(img_src)), self.D['di'](self.G(img_trg))
            ci_src, ci_trg = self.D['ci'](self.G(img_src)), self.D['ci'](self.G(img_trg))

            ci_src_shuffle = torch.index_select(
                ci_src, 0, torch.randperm(ci_src.shape[0]).to(self.device))
            ci_trg_shuffle = torch.index_select(
                ci_trg, 0, torch.randperm(ci_trg.shape[0]).to(self.device))

            MI_ds_ci_src = self.mi_estimator(ds_src, ci_src, ci_src_shuffle)
            MI_ds_ci_trg = self.mi_estimator(ds_trg, ci_trg, ci_trg_shuffle)
            MI_di_ci_src = self.mi_estimator(di_src, ci_src, ci_src_shuffle)
            MI_di_ci_trg = self.mi_estimator(di_trg, ci_trg, ci_trg_shuffle)

            MI = 0.25 * (MI_ds_ci_src + MI_ds_ci_trg + MI_di_ci_src + MI_di_ci_trg) * self.mi_coeff
            MI.backward()
            self.group_opt_step(['D_ds', 'D_di', 'D_ci', 'MI'])