图神经网络（四）图分类（2）基于层次池化的图分类

4.2 基于层次化池化的图分类

 本节以3中不同的思路介绍能够实现数据层次化池化的方案 [0] 。

 （1）基于 图坍缩（Graph Coarsening）的池化机制：图坍缩是将图划分成不同的子图，然后将子图视为超级节点，从而形成一个坍缩的图。这类方法正是借用这种方式实现了对图全局信息的层次化学习。

 （2）基于 TopK 的池化机制：对图中每个节点学习出一个分数，基于这个分数的排序丢弃一些低分数的节点，这类方法借鉴了CNN中最大池化操作的思路：将更重要的信息筛选出来。所不同的是，图数据中难以实现局部滑窗操作，因此需要依据分数进行全局筛选。

 （3）基于 边收缩（Edge Contraction）的池化机制：边收缩是指并行地将图中的边移除，并将被移除边的两个节点合并，同时保持被移除节点的连接关系，该思路是一种通过归并操作来逐步学习图的全局信息的方法。

4.2.1 基于图坍缩的池化机制

1.图坍缩

 假设对于图 $G$ ，通过某种划分策略得到 $K$ 个子图 $\{G^{(k)}{\}}_{k=1}^K$ ，$N_k$ 表示子图 $G^{(k)}$ 中的节点数，${\Gamma }^{(k)}$ 表示子图 $G^{(k)}$ 中的节点列表。

图4-1 图坍缩实例

 下面我们给出图坍缩中的两个比较重要的矩阵：

 第一个是簇分配矩阵 $S\in R^{N\times K}$，其定义如下：$S_{ij}=1$ 当且仅当 $v_i\in {\Gamma }^{(j)}$ 。

 例如，在图4-1所示的图坍缩示例中，我们将图 $G$ 划分成两个簇，这两个簇对应了图坍缩之后的两个超级节点，其中 ${\Gamma }^{(1)}=\{v_1,v_2,v_3\}$ ，${\Gamma }^{(2)}=\{v_4,v_5,v_6\}$ 。因此：
$$S=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\\ 0& 1\\ 0& 1\\ 0& 1\end{array}\right]$$
 下面我们来考察一下 $S^{\text{T}}AS$ 的意义：由于 $S^{\text{T}}$ 的第 $i$ 行表示的是所有属于第 $i$ 个簇的节点，依据矩阵乘法可知，$(S^{\text{T}}A{)}_{ij}$ 表示的是第 $i$ 个簇内所有与节点 $v_i$（全图中的第 $j$ 个节点）有关联的连接强度之和。同理可推，$((S^{\text{T}}A)S{)}_{ij}$ 反映了第i个簇与第j个簇的连接强度。如图4-1中的例子：
$$\begin{array}{rl}{S}^{T}AS& =\left[\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\end{array}\right]\left[\begin{array}{cccccc}0& 1& 1& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 1& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 1\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 1& 1& 0\end{array}\right]\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\\ 0& 1\\ 0& 1\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cccccc}2& 2& 2& 1& 0& 0\\ 0& 0& 1& 2& 2& 2\end{array}\right]\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\\ 0& 1\\ 0& 1\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cc}6& 1\\ 1& 6\end{array}\right]\end{array}$$
 如果我们令：
$$A_{\text{coar}}=S^{\text{T}}AS$$
 $A_{\text{coar}}$ 描述了图坍缩之后的超级节点之间的连接强度，其中包含了超级节点自身内部的连接强度，如果只考虑超级节点之间的连接强度，我们可以设置 $A_{\text{coar}}[i,i]=0$ 。

 第二个是采样算子，$C\in R^{N\times N_k}$ ，其定义为：$C_{ij}^{(k)}=1$ ，当且仅当 ${\Gamma }_j^{(k)}=v_i$ 。

 其中 ${\Gamma }_j^{(k)}$ 表示列表 ${\Gamma }^{(k)}$ 中的第 $j$ 个元素。$C$ 是节点在原图和子图中顺序关系的一个指示矩阵。比如上例中的：
$$C^{(1)}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],C^{(2)}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
 假设定义在 $G$ 上的一维图信号为 $x\in R^N$ ，下列两式分别完成了对图信号的下采样与上采样操作：
$$x^{(k)}=(C^{(k)}{)}^{\text{T}}x;\bar{x}=C^{(k)}{x}^{(k)}$$
 上述左式完成了对图信号在子图 $G^{(k)}$ 上的采样（切片）功能；右式完成了子图信号 $x^{(k)}$ 在全图的上采样功能，该操作保持子图中节点的信号值不变，同时将不属于该子图的其他节点的值设为 $0$ 。显然，该采样算子也适用于多维信号矩阵 $X\in R^{N\times d}$ 。

 有了采样算子的定义，对于子图 $G^{(k)}$ 的邻接矩阵 $A^{(k)}\in R^{N_k\times N_k}$ ，可以通过下式获得（事实上，$A^{(k)}$ 也可以通过对 $A$ 进行矩阵的双向切片操作获得）：
$$A^{(k)}=(C^{(k)}{)}^{\text{T}}A{C}^{(k)}$$
 根据上式可以得到上面例子中第一个簇内的邻接矩阵：
$$\begin{array}{rl}{A}^{(1)}& =(C^{(1)}{)}^{\text{T}}A{C}^{(1)}\\ & =\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right]\left[\begin{array}{cccccc}0& 1& 1& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 1& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 1\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 1& 1& 0\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\\ & =\left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 1\\ 1& 1& 0\end{array}\right]\end{array}$$
 通过上述两个矩阵可以确定簇内的邻接关系以及簇间的邻接关系。进一步来讲，如果能够确定簇内信号的融合方法，将结果表示为超级节点上的信号，那么我们迭代式地重复上述过程，就能获得越来越全局的图信号了。图4-2所示为图坍缩与GNN结合的过程：该图展示了一个经过 $3$ 个池化层最后坍缩成一个超级节点，然后进行图分类任务的GNN模型。图中相同颜色的节点被划分到一个簇上，形成下层的一个超级节点，在得到最后一个超级节点的特征向量之后，紧接着使用了一个三层的MLP网络进行图分类任务学习。

图4-2 图坍缩与GNN结合的过程 [2]

2.DIFFPOOL

 DIFFPOOL [1] 是首个将图坍缩过程与GNN结合起来进行图层面学习任务学习的算法。DIFFPOOL提出了一个可学习的簇分配矩阵。具体来说就是，首先通过一个GNN对每个节点进行特征学习，然后通过另一个GNN为每个节点学习出所属各个簇的概率分布：
$$\begin{array}{rl}& Z^{(l)}={\text{GNN}}_{l,\text{embed}}(A^{(l)},H^{(l)})\\ & \\ & S^{(l)}=\text{softmax}({\text{GNN}}_{l,\text{pool}}(A^{(l)},H^{(l)}))\end{array}$$ 其中 $A^{(l)}\in R^{n^{(l)}\times n^{(l)}}$ ，$S^{(l)}\in R^{n^{(l)}\times n^{(l+1)}}$ ，$n^{(l)}$ 表示第 $1$ 层的节点数，$n^{(l+1)}$ 表示第 $(l+1)$ 层的节点（簇）数，相较于上面例子中 $S$ 矩阵的硬分配，这里面学习出来的 $S$ 矩阵是一个软分配器，其值表示节点被分配到任意一个簇的概率，由于概率值不为 $0$ ，因此这是一个下层超级节点到上层所有节点之间的全连接结构。 ${\text{GNN}}_{l,\text{embed}}$、${\text{GNN}}_{l,\text{pool}}$ 是两个独立的 $\text{GNN}$ 层，二者的输入相同，但是参数不同，学习的目的不同。需要强调一点的是，对于最后一层的簇分配矩阵，我们需要直接将该矩阵固定成一个全 $“1”$ 的矩阵，这是因为，此时需要将图坍缩成一个超级节点，由此获得图的全局表示。

 有了上述两个十字的输出结果，我们可以对图进行坍缩：
$$\begin{array}{rl}& H^{(l+1)}={S^{(l)}}^{\text{T}}{Z}^{(l)}\\ & \\ & A^{(l+1)}={S^{(l)}}^{\text{T}}{A}^{(l)}{S}^{(l)}\end{array}$$
 将上述两个公式称为DIFFPOOL层 $(A^{(l)},Z^{(l)})\to (A^{(l+1)},H^{(l+1)})$ 。上面第一个式子是对簇内的信息执行融合操作，依据矩阵乘法的行向量计算方式，可以清楚地知道 ${S^{(l)}}^{\text{T}}{Z}^{(l)}$ 表示的是对簇内所有节点的特征向量进行加和处理。上面第二个式子即为簇间的邻接矩阵的计算。

 DIFFPOOL具有排列不变性：假设 $P\in \{0,1{\}}^{n\times n}$ 是一个任意的排列矩阵，只需要保证前面用到的GNN层是排列不变的，DIFFPOOL层就具有排列不变性，即：
$$\text{DIFFPOOL}(A,Z)=\text{DIFFPOOL}(PA{P}^{\text{T}},PX)$$

 排列矩阵的作用是对图中节点进行重排序，比如一个仅有两个节点相连的图，如果我们需要对两个节点的编号进行对调，则对应的排列矩阵 $P=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$ ，排列矩阵是正交的，即 $P^{\text{T}}P=I$ 。我们可以通过 $PX$、$PA{P}^{\text{T}}$ 来分别获得重排序之后的特征矩阵与邻接矩阵。

 证明：假设我们用到的GNN模型是GCN模型，GCN模型是满足排列不变的。设GCN的输出 $S=\text{GCN}(A,X)=\text{ReLU}({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}XW)$ ，现在使用 $P$ 对输入进行重排序，则：
$$\begin{array}{rl}\text{GCN}(PA{P}^{\text{T}},PX)& =\text{ReLU}((P{\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{P}^{\text{T}})(PX)W)\\ & =\text{ReLU}\left(P{\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}XW\right)\\ & =PS\end{array}$$ 这里用到了 $P^{\text{T}}P=I$ 的性质。由此可知，对GCN输入节点的顺序进行重排列，输出节点的顺序也会对应排列，但节点输出的表达向量并不会改变。因此，GCN是具有排列不变性的（也有成这种性质为排列等变性的，这是由于GCN所使用的聚合操作是排列不变的，可参考3.1节的相关内容）

 接着将此时GCN的各个输出值代入DIFFPOOL的式子中，即代入
$$\begin{array}{rl}& H^{(l+1)}={S^{(l)}}^{\text{T}}{Z}^{(l)}\\ & \\ & A^{(l+1)}={S^{(l)}}^{\text{T}}{A}^{(l)}{S}^{(l)}\end{array}$$中，得到：
$$\begin{array}{rl}& (PS{)}^{\text{T}}(PZ)=S^{\text{T}}Z\\ & \\ & (PS{)}^{\text{T}}(PA{P}^{\text{T}})(PS)=S^{\text{T}}AS\end{array}$$
 从所得结果可以看出来，这种重排列操作并没有改变DIFFPOOL的两个输出结果。于是式子
$$\text{DIFFPOOL}(A,Z)=\text{DIFFPOOL}(PA{P}^{\text{T}},PX)$$得证。

 总的来说，如果我们将GCN与DIFFPOOL合在一起看成一个层，对输入的图数据进行任意的重新编号，输出到下一层的特征矩阵与邻接矩阵并不会改变，这种性质是非常符合直觉的：节点是否重新排序并不应该影响节点聚合成簇的结果。

 有了上述DIFFPOOL层的定义，我们就可以模仿CNN分类模型的结构设计，不断组合堆叠GNN层与DIFFPOOL层，实现一种可导的、层次化池化的学习机制，并逐渐获得图的全局表示。可能的图分类模型的结构在图4-2中给出。

3.EigenPooling

 EigenPooling [3] 也是一种基于图坍缩的池化机制，但是不同于本章介绍的其他方法，EigenPooling没有对图分类模型引入任何需要学习的参数，这种非参的池化机制与视觉模型中的各类池化层具有很高的类比性，如表4-1所示：

表4-1 EigenPooling与 视觉模型中的池化比较

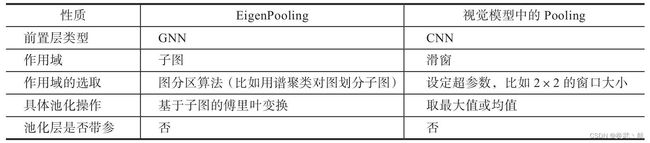
 从表4-1中我们可以再一次看到，GNN模型与CNN模型其实是殊途同归的。回到EigenPooling的具体过程中，其核心步骤在于作用域的选取以及池化操作，作用域是通过划分子图的方式对图进行分区得到的，这等价于图坍缩的过程，通过这一步可以得到新的超级节点之间的邻接矩阵，池化操作需要考虑的是对作用域内的信息进行融合，通过这一步可以得到关于新的拆机节点的特征矩阵。值得注意的是，在视觉模型中的池化操作的作用域都是规则的栅格结构，比如 $2\times 2$ 大小的滑窗，滑窗之间没有结构性的区别，而在图坍缩的子图上，作用域内的信息包含了结构信息与属性信息，特别是结构信息，不同的子图间有比较大的区别，因此结构信息的提取也是一个需要重点考虑的问题，EigenPooling就同时考虑了这两种信息并进行了融合。下面对上述两个步骤进行详细讲解。

（1）图坍缩

 与DIFFPOOL通过学习出一个簇分配矩阵来进行子图划分不同的是，EigenPooling中的图坍缩并没有给图分类模型引进任何需要学习的参数，其思路是借用一些图分区的算法来实现图的划分，比如选用谱聚类算法 [4] 。谱聚类是一类比较经典的聚类算法，其基本思路是先将数据变换到特征空间以凸显更好的区分度，然后执行聚类操作（比如选用Kmeans算法进行聚类），算法的输入是邻接矩阵以及簇数 $K$ ，输出的是每个节点所属的簇。值得注意的是，这里如果选用Kmeans算法进行聚类，那么簇的分配就是一种硬分配，每个节点仅能从属一个簇，这种硬分配机制保持了图坍缩之后的超级节点之间连接的稀疏性，与之相对的是DIFFPOOL中的软分配机制，节点以概率的形式分配到每一个簇中，导致超级节点之间以全连接的形式彼此相连，大大增加了模型的空间复杂度与时间复杂度。

 将图进行划分之后，我们调用
$$A_{\text{coar}}=S^{\text{T}}AS$$就可以得到超级节点间的邻接关系，当然，EigenPooling在这一步并没有考虑超级节点簇内的连接强度。

（2）池化操作

 在确定了子图划分以及相应的邻接矩阵之后，我们需要对每个子图内的信息进行整合抽取。在DIFFPOOL中选择了对节点特征进行加和，这种处理方式损失率子图本身的结构信息。而EigenPooling用子图上的信号在该子图上的图傅里叶变换来代表结构信息与属性信息的整合输出。从第一章的学习中我们知道，图信号的频谱展示了图信号在各个频率分量上的强度，它是将图的结构信息与信号本身的信息统一考虑进去，而得到的一种关于图信号的标识信息。因此，EigenPooling选用了频谱信息来表示子图信息的统一整合。下面给出其具体计算过程：

 假设子图 $G^{(k)}$ 的拉普拉斯矩阵为 $L^{(k)}$ ，对应的特征向量为 ${\mathbf{u}}_1^{(k)},{\mathbf{u}}_2^{(k)},\cdots ,{\mathbf{u}}_{N_k}^{(k)}$ ，然后，使用上采样算子 $C^{(k)}$ 将该特征向量（子图上的傅里叶基）上采样到整个图：
$${\tilde{\mathbf{u}}}_l^{(k)}=C^{(k)}{\mathbf{u}}_l^{(k)},l=1,\dots ,N_k$$
 为了将上述操作转换成矩阵形式，以得到池化算子 ${\Theta }_l\in R^{N\times K}$ ，我们将所有子图的第 $1$ 个特征向量按行方向组织起来形成矩阵 ${\Theta }_l$ ，即：
$${\Theta }_l=[{\tilde{\mathbf{u}}}_l^{(1)},\dots ,{\tilde{\mathbf{u}}}_l^{(k)}]$$
 需要注意的是，子图的节点数量是不同的，所以特征向量的数量也不同。用$N_{\text{max}}=\underset{k=1,\dots ,K}{\max }{N}_k$ 表示子图中的最大节点数。然后，若子图 $G^{(k)}$ 的节点数小于 $N_{\text{max}}$ ，可以将 ${\mathbf{u}}_l^{(k)}(N_k<l<N_{\text{max}})$ 设置为 $0\in R^{N_k\times l}$。有了池化算子的矩阵形式，池化过程可描述如下：
$$X_l={\Theta }_l^{\text{T}}X$$
 $X_l\in R^{K\times d}$ 是池化的结果。$X_l$ 的第 $k$ 行表示的是第 $k$ 个超级节点在 ${\Theta }_l$ 作用下的表示向量。按照该机制，我们共需要设计 $N_{\text{max}}$ 个池化算子。为了结合不同池化算子收集到的信息，我们可以采用按列方向拼接的方式，将各个结果连接起来：
$$X_{\text{pooled}}=[X_0,\dots ,X_{N_{\text{max}}}]$$ 其中 $X_{\text{pooled}}\in R^{K\times (d\cdot N_{\text{max}})}$ 是EigenPooling最终的池化结果。同第2.3节中论述的一样，作者在该文中也论证了显式场景下的图数据中低频信息的有效性。因此，为了提高计算效率，我们可以选择使用前 $H$ 个特征向量对应的池化结果，一般为: $$H\ll N_{\text{max}}：X_{\text{coar}}=X_{\text{pooled}}=[X_0,\dots ,X_H]$$
 上述计算都在矩阵层面进行，如果将计算回到向量形式上，我们可以更加清楚地看出EigenPooling是怎么利用图傅里叶变换对子图信息进行整合的。不失一般性，设全图上的信号为 $\mathbf{x}$ ，则式子
$$X_l={\Theta }_l^{\text{T}}X$$可描述为：
$$({\bar{\mathbf{u}}}_l^{(k)}{)}^{\text{T}}\mathbf{x}=({\mathbf{u}}_l^{(k)}{)}^{\text{T}}(C^{(k)}{)}^{\text{T}}\mathbf{x}=({\mathbf{u}}_l^{(k)}{)}^{\text{T}}{\mathbf{x}}^{(k)}$$
 其输出表示子图上对应的第 $l$ 个特征向量上的傅里叶系数。式子
$$X_{\text{pooled}}=[X_0,\dots ,X_{N_{\text{max}}}]$$的操作过程如图4-3所示：

图4-3 EigenPooling中子图上的图傅里叶变换

 图4-3中原图被划分成蓝、红两个子图，由于 $N_{\text{max}}=4$ ，所以输出矩阵为 $R^{2\times 4}$ ，每行表示的是在该子图信号上的前 $4$ 个图傅里叶系数。

 同DIFFPOOL一样，如果EigenPooling的前置GNN层选用GCN的话，EigenPooling整体也将具有排列不变性，具体证明可以从GCN、图坍缩、池化操作3个过程着手，其证明过程与DIFFPOOL的证明类似，这里不再赘述。

 总的来说，EigenPooling作为一种不带任何学习参数的池化机制，可以非常方便地正和岛一般dGNN模型中，实现对图信息的层次化抽取学习。与DIFFPOOL相比，其主要修饰在于保持了超级节点之间连接东西属性，提高了计算效率，同时在进行池化操作时，兼顾了子图内的结构信息与属性信息，这种做法显然更加合理。

[1] Ying Z , You J , Morris C , et al.Hierarchical graph representation learning with differentiable pooling[C]//Advances in Neural Information Processing Systems.2018：4800-4810.

[2] Ying Z，You J，Morris C，et al.Hierarchical graph representation learning with differentiable pooling[C]//Advances in Neural Information Processing Systems.2018：4800-4810.

[3] Ma Y，Wang S，Aggarwal C C，et al.Graph Convolutional Networks with EigenPooling[J].arXiv preprint arXiv：1904.13107，2019.

[4] Von Luxburg U.A tutorial on spectral clustering[J].Statistics and computing，2007，17（4）：395-416.

4.2.2 基于TopK的池化机制

 4.2.1节中介绍的基于图坍缩的池化机制，是一个节点不断聚合成簇的过程，而本节要介绍的基于 TopK 的池化机制，是一个不断丢弃节点的过程，其抓住的是图不同尺度的信息。和CNN中基于局部滑窗的池化操作不同的是，TopK池化将作用域放到全图节点上。具体来说，首先设置一个表示池化率的超参数 $k,k\in (0,1)$ ，接着学习出一个表示 节点重要度 的值 $\mathbf{z}$ 并对其进行降排序，然后将全图中 $N$ 个节点下采样至 $kN$ 个节点。用公式表示如下：
i = top-rank ( z , k N ) X ′ = X i , ∶ A ′ = A i , i \begin{aligned}&\boldsymbol{i}=\text{top-rank}(z,kN)\\ \\ &\boldsymbol{X}'=\boldsymbol{X}_{i,∶}\\ \\ &\boldsymbol{A}'=\boldsymbol{A}_{i,i}\end{aligned} ​i=top-rank(z,kN)X′=Xi,∶​A′=Ai,i​​
 ${\mathbf{X}}_{i,:}$ 表示按照向量i的值对特征矩阵进行切片，${\mathbf{A}}_{i,i}$表示按照向量i的值对邻接矩阵同时进行行切片与列切片。不同于DIFFPOOL，若将 $N$ 个节点分配给 $kN$ 个簇，会使得模型需要 $k{N}^2$ 的空间复杂度来分配簇信息，而基于TopK的池化机制，每次只需要从原图中丢弃 $(1-k)N$ 的节点即可。

 关于如何学习节点的重要度，引文 [5] 和引文 [6] 分别给出了不同的方法。在引文 [1] 中，作者为图分类模型设置了一个全局的基向量 $\mathbf{p}$ ，将节点特征向量在该基向量上的投影当作重要度：
$$\mathbf{z}=\frac{X\mathbf{p}}{\Vert \mathbf{p}\Vert }$$
 这样的一个投影机制，具有以下双重作用：

 （1）可以以投影的大小来确定 TopK 的排序；

 （2）投影大小还起到了一个梯度门限的作用，投影较小的节点仅有较小的梯度更新幅度，相对地，投影较大的节点会获得更加充分的梯度信息。

 全部细节用公示表示如下：
$$\begin{array}{rl}& \mathbf{z}=\frac{X\mathbf{p}}{\Vert \mathbf{p}\Vert },\mathbf{i}=\text{top-rank}(\mathbf{z},kN)\\ & \\ & {\mathbf{X}}^{\prime }=(X\odot \text{tanh}(\mathbf{z}){)}_{i,:}\\ & \\ & {\mathbf{A}}^{\prime }={\mathbf{A}}_{i,i}\end{array}$$
 在特征矩阵的更新中点乘了一个 $\text{tanh}(\mathbf{z})$ ，这相当于利用节点的重要度对节点特征做了一次收缩变换，进一步强化了对重要度高的节点的梯度学习。该文将上述过程称为 gpool层 。

 相较于基于图坍缩的池化机制对图中所有节点不断融合学习的过程，gpool层采取了层层丢弃节点的做法来提高远距离节点的融合效率，但是这种做法会使得其缺乏对所有节点进行有效信息融合的手段。因此，为了实现上述目的，作者选择在每一个gpool层之后跟随一个读出层，实现对该尺度下的图的全局信息的一次性聚合。读出层的具体实现方式是将全局平均池化与全局最大池化拼接起来：
$$\mathbf{s}=\frac{1}{N}\sum _{i=1}^N{\mathbf{x}}_i^{\prime }||\underset{i=1}{\overset{N}{\max }}{\mathbf{x}}^{\prime \prime }$$
 最终，为了得到全图的表示，将各层的 $\mathbf{s}$ 相加：
$$\mathbf{s}=\sum _{l=1}^L{\mathbf{s}}^{(l)}$$
 图4-4给出了一种可能的模型结构：

图4-4 基于TopK池化的图分类模型结构

 图4-4中的模型使用了两层gpool层，相应地也设置了两层读出层，之后对两层读出层的输出进行加和得到全图的向量表示，然后送到一个MLP里面进行图分类的任务学习。

 关于丢弃节点的池化机制，引文 [2] 给出了一种新的方式：自注意力图池化（SAGPool），该方法使用了一个GNN对节点的重要度进行学习，相较于gpool全局基向量的设计，这种基于GNN的方式更好地利用图的结构信息对节点的重要度进行学习。在该文中，作者也基于SAGPool层与读出层设计了两套高效的图分类模型，这一部分的细节，我们放到相应的实战中去讲解，这里不再赘述。

[1] Cangea C , VeličkovićP , JovanovićN , et al.Towards sparse hierarchical graph classifiers[J].arXiv preprint arXiv: 1811.01287, 2018.

[2] Lee J , Lee I , Kang J.Self-Attention Graph Pooling[J].arXiv preprint arXiv: 1904.08082, 2019.

[5] Cangea C，VeličkovićP，JovanovićN，et al.Towards sparse hierarchical graph classifiers[J].arXiv preprint arXiv：1811.01287，2018.

[6] Lee J，Lee I，Kang J.Self-Attention Graph Pooling[J].arXiv preprint arXiv：1904.08082，2019.

4.2.3 基于边收缩收缩的池化机制

 本节我们来介绍基于边收缩的池化机制——EdgePool [7] ，该方法将边收缩这一图论领域重要的变换操作与端对端的学习机制结合起来，实现了对图数据的层次化池化操作。概况地说，该方法迭代式地对每条边上的节点进行两两归并形成一个新的节点，同时保留合并前两个节点的连接关系到新节点上。这里存在一个问题：每个节点有多条边，但是每个节点只能从属于一条边进行边收缩，那么该如何选择每个节点所从属的边呢？为此，EdgePool对每条边设计了一个分数，依据改分数进行非重复式的挑选与合并。具体操作如下：

 对每条边，计算原始分数 $r$ ：
$$r_{ij}={\mathbf{w}}^{\text{T}}[{\mathbf{h}}_i||{\mathbf{h}}_j]+b$$
 由于每个节点选择哪条边，需要从其局部邻居出发进行考虑，所以，我们对原始分数沿邻居节点进行归一化：
$$s_{ij}={\text{softmax}}_j(r_{ij})$$
 得到上述分数之后，接下来对所有的 $s_{ij}$ 进行排序，依次选择改分数最高的且未被选中的两个节点进行收缩操作。细节如图4-5所示：

图4-5 EdgePool过程 [1]

 在图4-5中，a 图计算量图中每条边的原始分数 $r$ ，对于该无向图，我们将方向进行了双向复制，对于有向图则仅需安防箱进行后续操作，b 图计算了 $e^r$ ，c 图沿着入边方向对每个节点进行归一化操作，图中加黑的边表示被选中的进行收缩的边。需要注意的是，在确定 $⟨v_2,v_1⟩$ 边的时候，尽管 $⟨v_2,v_3⟩$ 边上具有更高的分数 $0.8$ ，但是 $v_3$ 节点已经被选择与 $v_4$ 节点进行合并，因此选择分数次高的 $⟨v_2,v_1⟩$ 边进行收缩，d 图展示了合并之后的结果。

 合并之后的节点特征，可以使用求和的方式表示：
$${\mathbf{h}}_{ij}=s({\mathbf{h}}_i+{\mathbf{h}}_j),s=\max (s_{ij},s_{ji})$$
 其中 ${\mathbf{h}}_{ij}$ 表示 $v_i$ 与 $v_j$ 节点合并后的新节点的特征向量，在计算该值的时候，与前面诸多方法一样，同样使用了分数 $s$ 对节点特征进行了收缩处理。如果边上由特征需要处理的话，$s_{ij}$ 与 $h_{ij}$ 的计算可以建立在RDF三元组之上，具体形式读者可自行思考。

 EdgePool与DIFFPOOL一样，都是不断对图中所有节点进行融合学习，不同的是DIFFPOOL需要自行设置聚类簇数，而EdgePool利用边收缩将节点归并比率严格控制在 $0.5$ ，另外，正是因为利用了边收缩的原理，EdgePool仅将相近的邻居节点进行归并，这种做法具有如下优点：节点的融合操作都是从边进行的，这契合了图的结构信息，更加合理；同时该操作也保留了融合之后途中连接的稀疏性，空间复杂度更低。作为一种端对端的池化机制，EdgePool也可以被广泛地整合到各个GNN模型中，已完成对图分类任务的学习。

[1] Diehl F.Edge Contraction Pooling for Graph Neural Networks[J].arXiv preprint arXiv: 1905.10990, 2019.

[7] Diehl F.Edge Contraction Pooling for Graph Neural Networks[J].arXiv preprint arXiv：1905.10990，2019.

[0] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社.