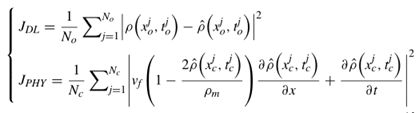基于物理信息深度学习的交通状态估计：以LWR和CTM模型为例

1.文章信息

本次介绍的文章是2022年发表在IEEE Open Journal of Intelligent Transportation Systems的一篇名为《Physics-Informed Deep Learning for Traffic State Estimation: Illustrations With LWR and CTM Models》的文章，该文章应用物理信息深度学习方法估计交通状态。

2.摘要

我们提出了一种物理信息深度学习（PIDL）方法来解决交通状态估计（TSE）中数据稀少和传感器噪声的挑战。PIDL用交通流理论的知识加强了深度学习（DL）神经网络，以准确估计交通状态。

物理信息的先验知识，即交通流理论在训练过程中起着正则化的作用。我们用两个常用的交通流模型—Lighthill-Whitham-Richards（LWR）模型和元胞传输模型（CTM）来说明所提出的方法的实施。LWR用Greenshields和inverse-lambda基本图实现，而CTM模型可用任何基本图实现。两个案例研究通过重建道路速度数据验证了该方法。案例研究-I模拟车辆运行场景，人为生成类似于路边设备捕获的网联和自动驾驶车辆的轨迹数据。案例研究-II采用NGSIM数据，模拟少量观测数据。实验结果表明，本文提出的PIDL方法在训练数据量较少的情况下，在状态估计方面取得了良好的效果，说明PIDL即使在输入稀少的情况下，也能够及时和准确地估计交通状态。

3.介绍

交通状态变量例如自由流速度f，平均速度v和车辆密度ρ可以显示道路上的交通状态，通过测量这些变量值，城市规划者和决策者可以感知拥堵程度，了解交通需求，甚至识别道路网络的拥堵和瓶颈。但是由于传感器安装成本和测量噪声等问题，交通管理和规划所需的这些关键数据通常很少，且精度还会受到影响。因此本文要解决的问题是如何利用有限且存在噪声的数据来实时获得清晰的交通状态。

交通状态估计指的是填补交通测量空白并描述路段交通状态的方法，即使用部分观察到的交通数据推断路段的交通状态。交通状态估计分为模型驱动和数据驱动方法。模型驱动方法将交通流理论中的模型用于交通状态预测，已经提出了元胞传输（CTM）、ARZ和LWR等模型来表示交通流。但是交通流模型只能在一定程度上表示交通状态数据间的关系，导致在模型选择不当和校准不佳的情况下得到较差的预测结果。随着统计方法和机器学习的进步，数据驱动方法已成为交通状态估计的另一种重要方法。数据驱动方法采用历史交通观测数据来预测交通状态。然而当前基于机器学习的方法过度依赖于获得的历史数据，在不同的交通场景中应用时会产生过拟合现象。

针对上述不足，本文提出了一种物理信息深度学习（PIDL）方法。该方法将深度学习和交通流理论相结合，能够利用有限且存在噪声的数据来实时获得清晰的交通状态。本文通过LWR模型和CTM模型来说明如何运用提出的PIDL方法，最终通过两个案例验证其有效性。

4.模型

方法概述

PIDL方法将收集到的交通状态数据集拆分为训练和测试数据集后，通过训练集预测交通状态变量（速度、密度和流速），并根据预测结果计算预测损失和物理损失，预测损失指训练结果与真实值的差异，物理损失指预测结果不符合交通流模型而导致的误差。神经网络通过将不符合交通流模型的误差添加到损失函数中来获得交通流模型知识。如果预测损失和物理损失之和大于指定阈值，则重复训练迭代。否则，神经网络就将预测结果作为输出。在模型中还设置了最大迭代次数来防止在总成本没有变化的情况下一直训练。模型步骤如下图所示。损失函数的设计是PIDL的主要组成部分之一。接下来说明如何设计LWR和CTM交通流模型的损失函数。

LWR模型损失函数

本文使用Greenshields和inverse-lambda基本图说明LWR模型，并给出损失函数公式。LWR模型表达式如下式所示，该式满足交通流守恒定律，称为LWR交通流偏微分方程。

Greenshields基本图描述了交通状态变量之间的关系，如下式所示，其中ρm是堵塞密度，vf是自由流速度。

Greenshields模型如下图所示。

Inverse-lambda基本图描述的交通状态变量之间的关系如下式所示，当交通密度达到ρc时，道路通行能力会下降，因此qc1和qc2分别是通行能力下降前后的值。

Inverse-lambda模型如下图所示。

LWR模型损失函数包含两部分。1）预测损失，用JDL表示。2）物理损失，用JPHY表示。预测损失应用于路段上具有真实观测数据的点，共有No个。物理损失可以应用于路段上的任何点，共有NC个，用来验证预测结果是否符合LWR模型。

1.LWR和Greenshield模型

Greenshields基本图描述的密度ρ和交通流q之间的关系将LWR模型表示为：

因此，进一步将预测损失JDL和物理损失JPHY表示为下式，其中(xj, tj) 是通过PIDL方法的DL分量估计的密度。

2.LWR和Inverse-Lambda模型

用inverse-lambda基本图描述的密度ρ和交通流q之间的关系将LWR模型表示为：

JDL与Greenshields模型相同，而物理损失被分为两个部分，共有NC1和NC2个点，分别代表自由流区域和拥堵区域。C1点处的密度预测值，C2点处的密度预测值。

为了在训练PIDL神经网络的同时结合交通流模型，PIDL的损失函数由预测损失JDL和物理损失JPHY组成。引入超参数μ来调整JDL和JPHY的权重，PIDL方法的损失函数为：

CTM模型损失函数

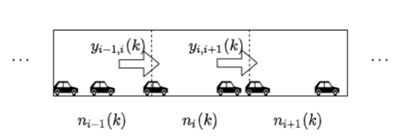
元胞传输模型（CTM）是一种离散化模型，将道路划分为连续的均匀路段（小区）来表示交通量，模型示意图如下图所示。

路段之间的车辆流量和路段中的车辆数量符合下式，其中ni(k)表示时间步长k处路段i中的车辆数，yi−1，i(k)表示时间步长k处路段i-1到路段i的车流量。

考虑下图所示的交通状态的时空表示，其中颜色表示交通状态值的变化。假设N1和N2分别是在空间和时间中离散道路密度后的网格数量，则N1*N2是待估计网格点的总数。CTM模型损失函数中的物理损失如下式所示：

假设每个时间步长的路段密度ρ相同，路段间每个时间间隔的流速q也相同，则。因此，使用CTM的预测损失和物理损失如下，其中路段i-1和路段i间的流速qi-1,i可用Godunov的数值格式进行计算。

5.案例分析

案例Ⅰ

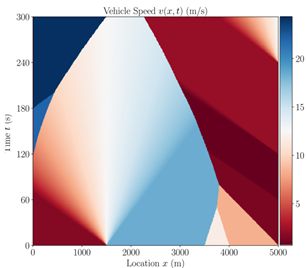
案例I模拟车辆运行场景，使用Lax-Hopf方法人为生成类似于路侧设备捕获的网联和自动驾驶车辆的轨迹数据(CAVs)。模拟路段长度为5000m，持续300秒(x，t∈ [0, 5000] × [0, 300])。 数据集的空间粒度为5米，时间粒度为1秒(Δx=5，Δt=1)。在这种情况下，速度场v(x，t)是神经网络的学习目标。给定一系列初始条件后，实验合成数据集如下图所示，其中车辆速度-密度关系符合Greenshield基本图。

本案例研究旨在利用路侧设备收集的CAV数据来估计速度场。假设路侧设备在路段上每1000米部署一次，则在5000米的道路上安装了6个路侧设备（第一个安装在初始位置x=0）。路侧设备的通信范围假定为300米。也就是说，CAV在x∈ [0，300]可以被第一个路侧设备捕获，第二个路侧设备可以记录在x∈ [700, 1300] 传输的CAV数据。

PIDL方法采用全连接神经网络，优化算法为LM-BFGS算法，最大学习迭代次数为5000次，为了在性能上与PIDL进行比较，本案例研究中还训练了一个具有相同结构的深度学习（DL）神经网络，但其损失函数中并未加入物理损失。

本文对交通流中CAVs的不同渗透率进行分析，1%渗透率则指车辆总体由1%的CAVs和99%的常规车辆组成。案例采用计算时间和2误差来评估PIDL方法的有效性。每个神经网络的性能用3个不同采样种子获得的训练数据集进行3次评估。同时还假设有10%的数据丢失，因此路侧设备通信范围内90%的传输数据被记录。

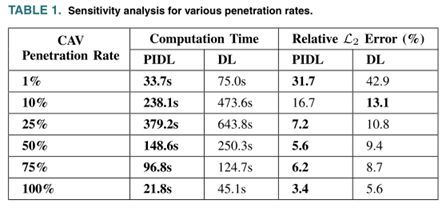
在不同CAVs渗透率下的预测结果如下表所示，加粗的表示PIDL方法效果更好。

借助交通流理论，PIDL明显比DL效果更好。同时随着CAV车辆的增加，训练数据的可用性越来越高，PIDL和DL的收敛时间都在减少（当CAV渗透率超过25%时）。这表明，有了丰富的训练数据，预测任务变得越来越简单，两个神经网络（PIDL和DL）都能够在更短的时间内产生结果。

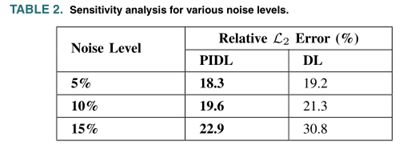
最后，本案例对训练数据中的噪声程度进行敏感性分析，以验证PIDL和DL的性能。即使使用了最好的可用传感技术，也必须考虑观测到的交通状态的不精确性。在给定合成数据集的情况下，本案例将训练数据与4级高斯噪声进行融合，并比较10%CAV渗透率场景下的性能。结果如下表所示。

实验结果表明，在有噪声的数据场景下，PIDL优于DL，并且随着噪声级别的增加，差异更加明显。

案例Ⅱ

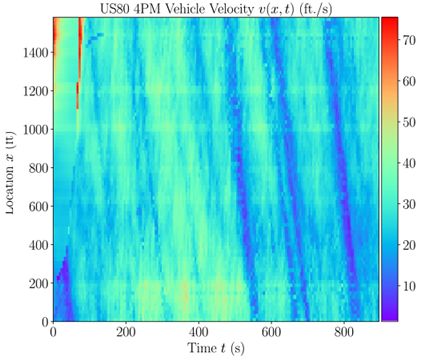
案例Ⅱ采用NGSIM数据集，该数据包含许多道路上的真实数据，本文选择在加利福尼亚埃默里维尔州80号州际高速公路（I-80）上收集的车辆轨迹数据。路段长约1600英尺，车辆速度和位置信息从视频记录中提取。下图显示了2005年4月13日下午4:00至4:15在I-80高速公路上获得的15分钟车辆速度数据。数据空间粒度为20英尺，时间粒度为5s，计算每个网格中车辆的平均速度，得到由180个时间点和80个空间点组成速度数据。

案例Ⅱ通过NGSIM数据集研究PIDL预测交通状况的能力。仍然运用LWR模型，用Greenshields基本图表示交通状态变量之间的关系。在案例Ⅰ中，速度数据是使用已知参数值建立的，例如自由流速度vf和堵塞密度ρm。但是在案例Ⅱ中参数是未知的，需要估计。密度-速度关系如下图所示。

下表给出了自由流速度vf和堵塞密度ρm的估计值。需要注意的是，车辆密度ρ是加利福尼亚州埃默里维尔I-80高速公路5车道上车辆的总和。

从数据中随机选择训练样本（模拟获取的少量数据），提供不同时空位置的神经网络预测结果。

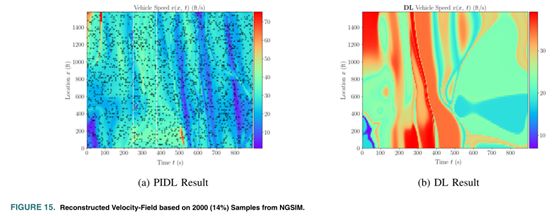
下图分别显示了使用1440（10%）和2000（14%）个训练数据预测的速度值，使用2误差评估预测结果的准确性。同时本文还假设计算能力有限，并且限制训练迭代次数最大为5000。在限制训练迭代次数情况下，PIDL仍优于DL。PIDL和DL收敛时的误差和训练迭代次数以及5000次迭代时的误差见下表。

虽然两个神经网络的结构和训练数据均相同，但损失函数的差异为PIDL提供了有效利用有限观测数据的独特优势。

6.结论

本文提出了一种物理信息深度学习（PIDL）方法来进行交通状态估计（TSE）。结合交通流的基本规律和深度学习方法，PIDL方法能够利用稀疏交通数据准确并及时地估计交通状态。PIDL方法使用LWR和CTM模型与Greenshields、Daganzo和Inverse-lambda基本图相结合。最后通过两个案例来验证PIDL方法的有效性。结果表明，PIDL方法能准确估计交通状态，并且优于DL方法，特别是数据稀疏和数据存在噪声的情况下。未来的工作应该考虑交通流模型参数的同步估计。

Attention

欢迎关注微信公众号《当交通遇上机器学习》！如果你和我一样是轨道交通、道路交通、城市规划相关领域的，也可以加微信：Dr_JinleiZhang，备注“进群”，加入交通大数据交流群！希望我们共同进步！