《Raytracing In One Weekend》学习笔记 Chapter 1、2、3、4、5、6、7、8、9、10、11、12、13
根据师兄推荐,打算从 Peter Shirley 的《Ray Tracing in OneWeekend》等系列图书入门光线追踪,学习过程中记录了一些经验总结笔记。这些笔记中包含了学习过程中遇到的一些知识理解以及编程相关的问题,如今记录下来,总结经验,加深印象。
Chapter 1. Overview
第一章介绍了作者将会使用c++进行编码,可以使用轻量级的IDE,甚至包括Codeblocks,这里我使用了Clion(通过教育网邮箱登录可以免费使用),比较轻量,而且代码管理也很方便。安装好Clion后记得配置一下C++环境。
作者喜欢在敲代码的过程中学习这些知识,我也很赞同。但是当一些代码提供可用时,虽然不好理解,推荐大家可以毫不留情的测试使用,这也是学习的一个过程。
Chapter 2. Output an Image
这一章主要教大家如何从无到有输入一幅rgb图像。图像采用ppm格式(wiki百科上有具体介绍,很详细,推荐看一下) 存储,构造过程和输出过程都十分简单。
比较有用的一点是,这里推荐了另外一种输出图像的方式(任意格式的图像),那就是使用stb_image_write第三方库,方法十分简单,所用代码如下:
- 将stb_image_write.h头文件源码文件放到当前目录下,然后声明头文件并编码输入:
#include "vec3.h" // 双引号应用的是程序目录的相对路径中的头文件
#include // 尖括号引用的是编译器类库路径中的头文件
#define STB_IMAGE_WRITE_IMPLEMENTATION // 使第三方库stb_image_write成为可执行的源码
#include "stb_image_write.h"
using namespace std;
int main() {
int nx = 200;
int ny = 100;
int channels = 3; // 代表rgb三通道,若为4则代表rgba四通道
unsigned char *data = new unsigned char[nx*ny*channels]; // 声明数组,用于存放像素rgb值
for(int j = ny -1; j >= 0; j--){
for(int i = 0; i < nx; i++){
vec3 col(float(i) / float(nx), float(j) / float(ny), 0.2);
int ir = int(255.99*col[0]);
int ig = int(255.99*col[1]);
int ib = int(255.99*col[2]);
data[(ny - j - 1)*nx*3 + 3 * i] = ir; // 计算出二维图像中的像素在一维数组中的对应位置,从第一行第一列开始
data[(ny - j - 1)*nx*3 + 3 * i + 1] = ig;
data[(ny - j - 1)*nx*3 + 3 * i + 2] = ib;
}
}
stbi_write_png("PNGOutput2.png", nx, ny, channels, data, 0); // 输出图像
return 0;
}
- 与stb_image_write相关的知识参见博客文章:简单易用的图像解码库介绍 —— stb_image,很实用。
Chapter 3. The vec3 Class
这部分创建了一个vec3向量类,用于创建、表示以及操作三维向量。
- 新增了一个有意思的点是inline内联函数,这部分内容c++课本上多有描述,可以解决一些频繁调用的函数大量消耗栈空间(栈内存)的问题。
- 此外还重载了c++中的运算符,用于向量的基本数学运算。如果你感觉心里没底最好的方式是找课本上的运算符重载实例练习一下,至少有个了解。
难度不大,不用惊慌。 - 关于c++编程有两点需要注意:
- 一是定义类时,创建了.h文件还需要再创建.cpp文件吗?其实不创建.cpp文件完全不影响编译,创建.cpp文件的主要目的是实现成员函数声明和定义的分离,方便代码管理(个人理解),当前项目相对来说是很轻量的,只需要创建一个.h文件就足够了(虽然博主也创建了.cpp文件,但是推荐只创建.h文件即可)。
- 二是可以通过条件编译实现再同一个项目中管理不同章节的代码,节省创建新项目的时间。这部分的内容有时间的话博主会另写一篇总结文章。
Chapter 4. Rays, a Simple Camera, and Background
这部分通过描述了射线的定义并创建了射线ray类,定义一个摄像机,以及创建一个颜色函数color来初步构建了一个光线追踪器,具有发射光线,计算光线与像素碰撞点的颜色的功能(demo中显示出了背景的颜色)。个人认为需要注意的有以下几点:
- 射线的数学定义函数需要理解(博主认为大家应该比较容易理解,需要注意的是初始时只需要起点和方向就能定义一条射线;后续章节中由于涉及到射线与模型相交,所以又引入了参数t,用于表示射线相交后有效部分的长度);
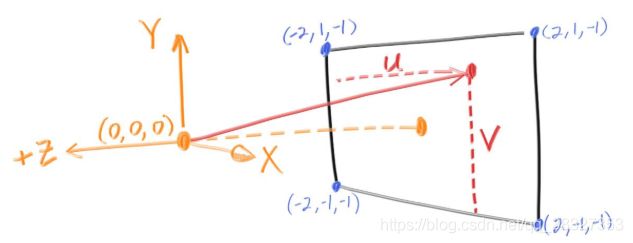
- 摄像机的位置很有意义(科普向),始终位于(0, 0, 0)原点处,向上与y轴正方向重合,向前朝向z轴的负方向(也就是看向z轴的负方向)。这里可以给大家普及一下,计算机图形学中一般是认为摄像机固定于上述的标准位置,那么可能有同学问了,现实世界中摄像机是会动的啊。这里需要解释一下,此处用到了物理的相对运动知识,也就是说,我们可以把摄像机的运动转换成模型的运动,对模型进行视图变换(也叫摄像机变换)从而得到运动后的模型状态信息,然后再进行渲染操作。变换过程中的数学知识很有趣,有兴趣的同学(你可能没时间看,但是我强烈推荐你在空闲看!),可以观看闫令琪GAMES101的第四课,视图变换部分内容(你很有可能会把前面的部分也看完)。
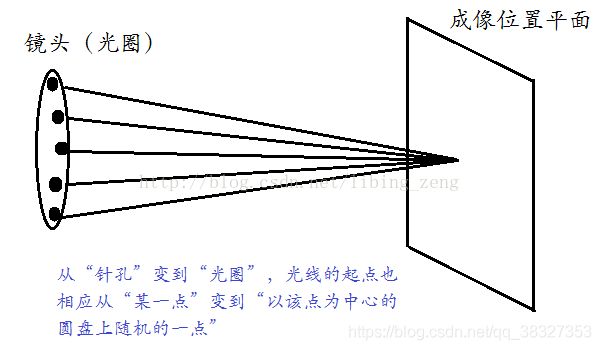
- 射线是由摄像机位置发出的,模拟了由人眼发出的视线,有多少条呢?目前我们是在for循环中规定了一个像素点对应一条,也就是有200*100条(可以想象一下,如果博主没推错的话就是对了);
- 射线与某物体(本章节只涉及背景)相交后,需要通过color函数计算一下颜色值,这就是该位置我们看到的颜色;
- 颜色是通过射线的方向向量单位化后的y分量映射后并进行插值得到的。解释一下,就是射线有一个方向向量,作者将该向量单位化,所以三个分量的取值范围都是(-1, 1);然后将对应的y分量从(-1, 1)映射到(0, 1)上(为啥是开区间?博主暂时没有考虑;映射的计算过程以y分量为例,为:0.5*(y + 1.0)),为啥插值到(0, 1)区间上?因为插值参数的范围需要是(0, 1),这个y分量映射之后就是插值参数t;最后进行插值操作:
// 返回插值后的颜色,从浅蓝色到白色之间进行插值;从上到下渐变的颜色同时对应了y从大到小(for循环规定的)的位置特性
return (1.0 - t)*vec3(1.0, 1.0, 1.0) + t*vec3(0.5, 0.7, 1.0);
// 特别注意,这个t和第五章中的t不是一回事;这里的t只代表插值参数,第五章中的t代表射线函数的中的一个变量(注意一下即可)
Chapter 5. Adding a Sphere
这一部分主要是在场景中定义了一个球体,然后判断射线与球体是否相交,如果相交了,将球体对应的颜色设置为红色。你可能对以下几个问题感到疑惑:
- 球体是怎么定义的?事实上,这里的球体只是在数学计算(射线与球体碰撞)中有所涉及,只是虚构了一个球体,仅有球心和半径的信息,目前并未创建球体实体(下一章将会创建球体类,充分利用c++面向对象的特点);
- 射线与球体是怎么碰撞的? 实际上是通过数学计算进行判断的。因为我们知道了球心和半径,所以可以写出球面坐标公式:

Cx/y/z代表了球心坐标,R为球半径,都是已知的。
实际上我们并不想用这个方程,我们想用的是球面坐标的向量表示方式,即:
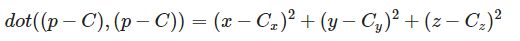
其中p为球面上的任意一个点(x, y, z),这个方程的数学含义是,球面上任一点与球心之差构成一个向量,这个向量和自己的点乘结果,是等于方程右侧式子的(单纯计算推出来的,dot表示点乘);而右侧的式子恰恰就是球面坐标公式的一部分,它等于R的平方,也就是说,我们得到了球面上任意一点的向量表示方式。
现在我们想计算球面有没有和射线发生碰撞,考虑到射线的参数表示为:p(t)=A+t∗B,p(t)表示射线上的任意一个点(x, y, z),A为射线起点坐标,B为射线的方向向量,t为参数变量,可以认为A、B是已知的,仅t未知。
所以要想计算球面和射线有没有相交,直接将射线带入球面方程即可,如果你思路很清晰的话,会发现代入后仅剩下一个变量,那就是t,带入后得到了关于t的一元二次方程。博主通过向量的结合率将射线方程代入球面方程后推导了一下,最终得出了下面的方程:

这就是射线与球面的相交方程,仅含有t这一个未知数,所以可以通过计算相应的一元二次方程的判别式来判断有没有解,若有解,有几个解(1个or2个)。在这一章里,我们只是判断了有没有解的情况,若有解,代表有交点,然后我们将对应位置处的像素赋值为红色(问:怎么找到这个像素的呢?其实阅读源码不难发现这里有这么一个性质,那就是图像像素和射线存在一一对应的关系,也就是说,根据像素的u、v坐标确定了一条射线,这条射线和模型如果相交,那么这个像素就要赋值红色;若未相交,赋值为计算得到的背景色;所以要赋值的这个像素根本就不需要找,它就是我们最初的图像上某个具体位置的像素啊);若无解,表示射线与模型没有交点,射线投向了背景,我们需要将对应位置处的像素赋值为插值计算出的背景色。 - 其实这一章还有个重大缺陷,那就是判断出来的有解的情况,可能对应着球在射线的负方向上,即t<0的情况,很显然摄像机后面的球是看不见的,下一章对这个缺点进行了改进,排除了t<0的情况。
Chapter 6. Surface Normals and Multiple Objects
这一部分分两个片段分别介绍了一些内容。
第一个片段介绍了球面法线的定义,以及如何可视化法线(通过颜色标识)。
- 球面法线定义为(射线与球面碰撞点 - 球心点),作者个人倾向于对其再进行单位化操作,因为这会对后续的着色提供方便。
- 可视化法线:球面上分布了无数的法线,每一条法线的x/y/z分量都不一定相同(由于我们获取的法线是进行单位化的,所以每一分量的取值范围为(-1, 1)),所以可以利用这个特征,将每一条法线的x/y/z分量映射到(0, 1)(r/g/b)上 (映射方法很简单,可以参看第六章color函数的源码),对应着像素颜色r/g/b的取值范围,从而表示像素点的颜色,实现法线的可视化。
第二个片段实现了在场景中通过链表的形式创建多个物体,用到了c++面向对象的知识。
- 这里构造了一个抽象类hittable,可以认为是一类被射线碰到的物体(这里作者认为会与面向对象中的对象混淆,所以换了一种命名方式,最后作者根据这个类中的虚函数hit(用来计算判断是否发生碰撞)命名了这个抽象类)。
- 这里还构造了sphere类,继承自抽象类hittable,并实现了父类中的虚函数hit的定义(你最好了解一下抽象类虚函数的基础知识,不用太深入)。这样的好处就是把不同的碰撞细节定义在了不同的物体类中,如果再添加一个其它类别的物体,比如说立方体(实际这本书并未涉及),我们可以把对应的判断碰撞方法写到该类的hit函数里,充分面向对象。
当前章节中还用到了多态的思想。指的是,声明hittable类型的链表,然后为该链表赋值为sphere类型的内容。简单的说,就是一句话:允许将子类类型的指针赋值给父类类型的指针。赋值之后,父对象就可以根据当前赋值给它的子对象的特性以不同的方式运作(摘抄自百度百科)。
关于最后的结果图:在最后的结果图中,你可能会问,**为啥大球是一片均匀的绿色的呢?**我的理解是大球太大了,导致我们看到的球面法线变化值不大,所以映射到颜色后,显示一片均匀的绿色。至于为啥是绿色,那是因为x/y/z对应的r/g/b值中,y分量比较大,所以g值大,显示绿色(个人理解)。
Chapter 7. Antialiasing
这部分讲的是如何实现Antialiasing抗锯齿,也叫反走样。
- 主要原理很简单,那就是通过计算周围像素的颜色平均值来得到当前像素的颜色,比如说在边界处具有很明显的前景色和后景色,要想获得平滑的边界,可以把前景色和背景色混合得到一个边界色,作为过渡,由于像素很小,所以不放大看的话,像素的锯齿感就消失了。作者在这里并没有考虑多层颜色的影响,给出的理由是对画面效果的提升不大。
- 实际编程过程中作者随机采样(这也是为啥用到随机函数的原因)了200个周围的像素点,最后取了一下平均值得到当前像素的颜色值。这就相当于在计算每一个像素点的颜色值时,在其周围随机发射了200条射线,并计算交点颜色,最后取平均。这就与先前章节中介绍的一个像素对应一条射线不一样了,读者需要注意。
Chapter 8. Diffuse Materials
Diffuse Materials 漫反射材质 让模型的视觉效果更逼真。
这部分开头作者做了一下声明,那就是作者将几何形状和材质分开了,而非一一对应,这会导致一些局限性。此外,漫反射材质本身不发光,只会反射周围的环境光,同时会将环境光混合调制成本身的色彩。光线在漫反射表面上的反射方向是随机的,如下图:

当然有些光线也可能会被吸收,表面越黑,吸收光线的能力越强。这也是黑色物体为啥黑的原因——因为它吸收光线,极少反射光线。
废话不多说,我们看看代码部分有哪些需要注意的。
- 如何模拟射线的随机反射?
- 先搞清楚为啥要模拟随机反射:因为根据漫反射材质随机反射光线的性质,光线照射到漫反射材质表面上时,会被表面吸收(当前章节不考虑)或随机反射到一个方向上,而且有可能会反射后再次反射(当然强度会衰减),如果这样考虑的话,渲染效果将会更加逼真,这是由真实世界中的物理规律决定的。
- 具体怎么做才能获取随机反射射线呢?作者在实现过程的一个步骤中采用了一个取巧的办法,叫舍弃法(理解起来很简单,博主就不多说了,但是博主认为这个方法有很大缺陷)。整体步骤描述如下:首先我们已经计算得到了射线与物体(这里主要是sphere)之间的交点,并且知道交点处物体表面的法线(是一个单位向量),所以如果我们在原点(0, 0, 0)处获取一个随机点(这个随机点位于以原点为球心的单位球体内,实际上demo程序中只计算了x/y/z各分量都为正的情况),那么,将该随机点(其实是以原点为起点的向量)与已知的交点坐标和法线向量相加,就可以得到一个新的随机点,这个点位于一个球体中,这个球体的半径为1,球心坐标为射线与sphere交点加上法线向量。也就是说,我们最终获得了位于单位半径球体中的一个随机点,这个随机点与射线和sphere交点之差,便是新的反射射线的方向,而交点就是反射射线的起点。至此,一条随机反射射线便构造出来了。

- 上面提到过,随机反射射线如果和物体碰撞还可以再次进行反射,但是不会无线反射下去,因为射线每反射一次,其强度便会衰弱一次(这里我们用衰弱系数描述),所以最后要么最后碰撞到背景,要么因为强度太弱无法继续反射。体现在demo程序中便是一个递归函数,上述两种中止情况便是递归的返回条件。
- 最后还需要注意两个问题:
- 颜色问题,生成的图片偏黑,矫正一下,理想的效果应该是浅灰色,为此我们可以对像素颜色分量分别进行开方处理,变相的增强了颜色的亮度(因为颜色分量是小数),前后对比效果图如下


- 编程问题,是浮点类型的t造成的,因为二进制计算机在判断相等时,是用范围来判断的。举个例子,对于float数据类型的实数,-0.0000001和0.0000001都被计算机认为是0,因此我们应该舍去负值(对应射线与球体交点在视线背面的情况),这样的操作去除了“阴影粉刺”现象(的确是这么称呼的。。。),效果图如下

代码中的MAXFLOAT表示单浮点数允许的最大值,这里博主没有找到它的头文件,不过博主在float.h中找到了FLT_MAX,可以用做替代。
Chapter 9. Metal
Metal 金属,这里指金属镜面反射材质。
在本章开始,作者表明打算建立一个抽象类material用作所有材质类的基类,它含有一个虚函数scatter,意思是散射。
可能有同学会产生一个问题,为啥在hittable.h中添加了这么一句:“class material;”,很明显是为了创建一个material类型的指针,由于没有涉及到构造函数的调用,所以允许这样做!其实博主还想问,为啥不先创建好了material类,然后直接引入该类的头文件呢?可能是为了在后面的编程过程中避免重复引用头文件吧。
在这部分创建了sphere类(继承自hittable基类),并实现了hit函数的定义,用于判断射线与球面是否相交,以及计算交点对应的t值(射线上的t)、计算交点坐标、计算交点处的法线、获取material指针,并将上述信息存储到hit_record结构体中,用于后续的射线散射计算。
在这部分创建了material的子类lambertian(用于表现漫反射),实现了scatter散射函数的定义,主要用于在相交后计算漫反射材质对应的随机反射射线。
在这部分同样创建了material的子类metal(用于表现金属镜面反射),同样实现了scatter散射函数的定义,不过这里的反射射线不再像漫反射那样具有随机方向了,而是有一定的数学规律,只要掌握向量点乘(dot)的基本知识和简单的三角函数计算就能推导出来(参见对应章节的教材讲解),唯一可能需要注意的是教材中描述的N(即法向量,法线),是一个单位向量,根据向量点乘公式计算时,N的模为1,所以计算被简化了(你应该明白我在说什么)。
下面的总结可能会比较复杂,建议先看电子版课本教材,同时对派生有一定理解,再来看下面这段总结:
原文中有一句英文可能不太好理解,但是翻译过来的意思是:当射线与球体表面相交时,hit_record结构体中的material指针就会被赋值从而指向一个具体的material指针,这个material指针纸箱相交球体的material属性,我们在mian函数中创建这个球体的时候就设置好了它的material属性。英语原文如下:
When a ray hits a surface (a particular sphere for example), the material pointer in the hit_record will be set to point at the material pointer the sphere was given when it was set up in main() when we start.
其实上面做的好处在于,我们想要通过一个物体链表来控制所有的场景模型物体,这个列表是hittable类型的,实际存放的其实是hittable的子类对象,这里用到了派生的思想(前面也说过)。这样的话可以使用for循环,对链表里的物体进行遍历,并执行统一的操作,如调用子类的成员函数hit判断是否相交,利用自身结构体成员hit_record中的material类型指针来调用对应材质的scatter散射函数,以此判断反射射线的具体情况(反射or折射,具体怎么反射or折射等等)。听起来可能比较复杂,但是如果你对面向对象的派生比较熟悉,相信你理解起来也不会那么复杂。
最后一部分内容与第八章模拟随机反射中的随机点相似,可以搭配着进行理解。
Chapter 10. Dielectrics
这部分引入了电介质材质。介绍几个术语:
dielectric 电介质
reflect 反射
refract 折射
Snell’s law 斯内尔定律,也就是折射定律
refractive index 折射率
啥是电介质材质?水、玻璃、钻石都是电介质(教材原话,老实说水是电介质吗,电介质不是不导电的吗Peter Shirley这里是不是应该改成空气、玻璃、钻石???还有另外一种理解,即这里的介质是指光线能够透过的介质,这样水、玻璃、钻石这些物体属于“电介质”就比较好理解了)。
电介质材质有啥特点?当一条光线穿过电介质材质时,会产生两条光线,一条是反射光线,一条是折射光线。在这一章我们假定一条光线将会随机的生成一条反射光线或者折射光线,即反射光线和折射光线不会由同一条射线产生(仅仅是在这里假定的)。相比而言折射光线的计算比较困难。
这部分还需要注意一个特殊情况,全反射。全反射是指,当入射角大于某一个固定值时,入射光线全部产生了反射光线,不再产生折射光线,有关定理和证明可以参见百度百科。
这一部分的难点主要在于折射光线的推导(也就是折射函数refract是怎么定义的)上,下面我们根据折射函数refract的具体定义进行分析:
bool refract(const vec3& v, const vec3& n, float ni_over_nt, vec3& refracted) const {
vec3 uv = unit_vector(v); // 入射光线的单位方向
float dt = dot(uv, n); // 入射光线与法线夹角的cos值
float discriminant = 1.0 - ni_over_nt*ni_over_nt*(1-dt*dt); // 折射光线的判别式(判断其是否存在),如何推导过来的?
if (discriminant > 0) { // 存在折射光线
refracted = ni_over_nt*(uv - n*dt) - n*sqrt(discriminant); // 计算折射光线的方向
return true;
} else // 不存在折射光线
return false;
}
- 结合注释我们知道了现在难点有两个,即:①折射光线的判别式是如何推导出来的,和②折射光线的方向如何计算。注意:ni_over_ni为入射介质折射率和出射介质折射率的比值。
- ①折射光线的判别式是如何推导出来的?当产生全反射时,是不存在折射光线的,难道我们需要计算全反射的临界角度吗?博主认为不是不可以,但是在教材中,作者用了这样一种方法:

- ②折射光线的方向如何计算? 推导过程可以参见博客光反射与折射向量方向计算详解(基于Ray Tracing in One Weekend这本书)。转换过程中你可能会遇到三角函数相关的问题,如:dot(uv, n) = -cos(入射角)(来自于demo源码),这一点涉及到三角函数的一个小知识,即cos(PI - θ) = - cosθ。
这部分的另外一个难点在于光线传播方向的判断,即光线是从空气射向物体,还是从物体内部射向空气,对应的代码及辅助理解的公式如下:
if (dot(r_in.direction(), rec.normal) > 0) { // 判断入射光线和法线之间的夹角角度,> 0 表示成锐角,从而推断出是从空气进入物体,还是从物体进入空气
outward_normal = -rec.normal; // 光线从物体准备射向空气
ni_over_nt = ref_idx; // 物体与空气的折射率之比
cosine = ref_idx * dot(r_in.direction(), rec.normal) / r_in.direction().length(); // 计算夹角的cos值
} else {
outward_normal = rec.normal; // 光线从空气准备射向物体
ni_over_nt = 1.0 / ref_idx; // 空气与物体的折射率之比
cosine = -dot(r_in.direction(), rec.normal) / r_in.direction().length(); // 计算夹角的cos值
}
本章最后几个问题:如何实现菲涅尔现象,schlick函数和反射系数在编码过程中的具体作用是啥?
- 其实shlick函数就是用来近似模拟菲涅尔现象的。通过shlick函数计算出一个反射系数来,然后根据反射系数以及一个随机数判断当前应该发出反射光线还是折射光线,从而模拟出菲涅尔现象。
另外一个问题,demo代码中cosine值需不需要乘上ref_idx?ref_idx是两种介质折射系数的比值,对于空气和水,这个比值为1.4,相对来说乘与不乘对整个函数的影响不是很大。总之这个问题目前博主还不太清楚,有待第二次阅读时进一步解决。
Chapter 11. Positionable Camera
Positionable Camera可以定位的摄像机。
在这部分作者对摄像机进行了定义,其中vup、u、v、w大家应该很容易理解对应的含义。
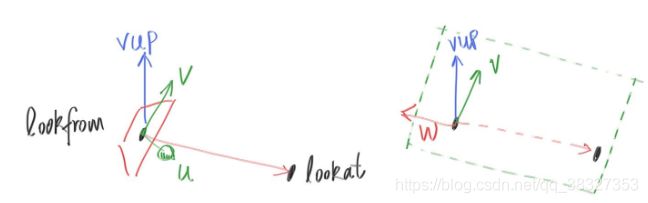
只是,vfov和aspect需要解释一下。
- vfov是指vertical field of view,即垂直可视角度;aspect为长宽比(aspect ratio),即屏幕的宽度/屏幕的长度(width/length)。当我们知道垂直可视角度和长宽比时,可以很容易的推出水平可视角度。这些概念在视口变换中有用到,视口变换是指将观测变换(包括视图变换也就是摄像机变换,以及投影变换(含正交变换和透视变换))之后的结果(是一个[-1, 1]的三次方的空间),变换到屏幕(是一个[0, width]x[0, height]的平面)上,后续将进行光栅化操作,这些知识和本书没有直接关系。
Chapter 12. Defocus Blur
Defocus Blur 焦散模糊,与摄影领域的景深有关,景深是指用摄像机进行摄影,对焦过后,焦点所在物体前后清晰的范围。通常来说,使用大光圈可以获得较小的景深,使用小光圈可以获得大景深。当物体位于景深范围外时,就会拍摄出模糊的照片,也就是焦散模糊,字面上看其实就是失焦导致的模糊(摄影也是博主的一门专业课)。


Chapter 13. Where Next?
这部分留下了一个项目案例,那就是生成图书的封面图。在这里博主提高了画面的分辨率(1920*1080)和采样数(400),场景模型生成函数如下:
hittable *random_scene(){
int n = 500;
hittable **list = new hittable*[n+1];
list[0] = new sphere(vec3(0, -1000, 0), 1000, new lambertian(vec3(0.5, 0.5, 0.5)));
int i = 1;
for (int a = -11; a < 11; a++) {
for (int b = -11; b < 11; b++) {
float choose_mat = random_double();
vec3 center(a+0.9*random_double(), 0.2, b+0.9*random_double());
if((center-vec3(4, 0.2, 0)).length() > 0.9) {
if (choose_mat < 0.8) { // 漫反射
list[i++] = new sphere(center, 0.2,
new lambertian(vec3(random_double()*random_double(),
random_double()*random_double(),
random_double()*random_double())));
} else if (choose_mat < 0.95) { // metal
list[i++] = new sphere(center, 0.2,
new metal(vec3(0.5*(1 + random_double()),
0.5*(1 + random_double()),
0.5*(1 + random_double())),0.5*random_double()));
} else { // 玻璃
list[i++] = new sphere(center, 0.2, new dielectric(1.5));
}
}
}
}
list[i++] = new sphere(vec3(0, 1, 0), 1.0, new dielectric(1.5));
list[i++] = new sphere(vec3(-4, 1, 0), 1.0, new lambertian(vec3(0.4, 0.2, 0.1)));
list[i++] = new sphere(vec3(4, 1, 0), 1.0, new metal(vec3(0.7, 0.6, 0.5), 0.2)); // f表示模糊系数,取值[0, 1]
return new hittable_list(list, i);
}
摄像机位置和朝向点参数设置如下:
vec3 lookfrom(13, 2, 3); // 摄像机位置
vec3 lookat(0, 0, 0); // 朝向点
有几点可能对你的项目产生帮助:
- ①采样一个像素点后接着输出到文件的效率太低了,可以使用一个data将像素rgb值存起来,最后输出。所以这里建议使用stb_image_write第三方库,具体使用方法第二章的经验总结部分已经讲过了。
- ②渲染一张高分辨率的图像实在是太慢了,建议编码估算渲染剩余图片像素消耗的时间。实现的过程很简单,首先计算第一次采样消耗的时间(提示:第三个for循环执行结束代表着第一次采样的计算结束),然后用这个时间间隔乘上剩余像素数量,便可得到渲染剩余图片像素需要的时间。可以调用time.h头文件中的clock函数用于获取一个时间,具体参考博客c/c++获取时间函数。
- ③你也根据遍历像素的个数来估算当前渲染任务的进度,很简单:
std::cout << "Process Bar:" << (ny - j) / float(ny) * 100.0f << "% "; // Process Bar 进度条
至此,博主将《Raytracing In One Weekend》学习过程中遇到的问题和经验总结了一下,部分内容带有强烈的主观判断,希望各位观众老哥大胆批评指正!~ 谢谢!~