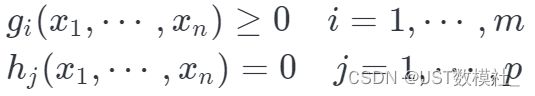数学建模常用算法—非线性规划

目录

模型的含义

问题转化为模型

模型建立

模型例题与求解

---

上篇我们学习了线性规划模型，这篇我们一起来学习一下非线性规划。非线性规划在工程、管理、经济、科研、军事等方面都有广泛的应用，为最优设计提供了有力的工具。

模型的含义

        非线性规划(nonlinear programming)具有非线性约束条件或目标函数的数学规划，是运筹学的一个重要分支。非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题，且目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是线性函数的情形则属于线性规划。

 问题转化为模型

         对于一些常见的问题，再把它归结成非线性规划问题时，一般要注意如下几点：

        （1）确定供选方案：首先要收集同问题有关的资料和数据，在全面熟悉问题的基础上，确认什么是问题的可供选择的方案，并用一组变量来表示它们；

        （2）提出追求目标：经过资料分析，根据实际需要和可能，提出要追求极小化或极大化的目标。并且，运用各种科学和技术原理，把它表示成数学关系式；

        （3）给出价值标准：在提出要追求的目标之后，要确立所考虑目标的“好”或“坏”的价值标准，并用某种数量形式来描述它。

        （4）寻求极限条件：由于所追求的目标一般都要在一定条件下取得极小化或极大化效果，因此还需要寻找出问题的所有限制条件，这些条件通常用变量之间的一些不等式或等式来表示。

模型建立

        对实际规划问题作定量分析，必须建立数学模型。建立数学模型首先要选定适当的目标变量和决策变量，并建立起目标变量与决策变量之间的函数关系，称之为目标函数。然后将各种限制条件加以抽象，得出决策变量应满足的一些等式或不等式，称之为约束条件。

        非线性规划问题三的一般数学模型可表述为求未知量 x1,x2,...,xn，使满足约束条件：

 

并使目标函数f(x1，…，xn)达到最小值(或最大值)。其中f，gi和hj都是定义在n维向量空间Rn的某子集D(定义域)上的实值函数，且至少有一个是非线性函数。

上述模型可简记为：

        其中x=(x1，…，xn)属于定义域D，符号min表示“求最小值”，符号s.t.表示“受约束于”。

        定义域D中满足约束条件的点称为问题的可行解。全体可行解所成的集合称为问题的可行集。对于一个可行解x*，如果存在x*的一个邻域，使目标函数在x*处的值f(x*)优于(指不大于或不小于)该邻域中任何其他可行解处的函数值，则称x*为问题的局部最优解(简称局部解)。如果f(x*)优于一切可行解处的目标函数值，则称x*为问题的整体最优解(简称整体解)。实用非线性规划问题要求整体解，而现有解法大多只是求出局部解。

 模型例题与求解

 MATLAB中非线性规划的数学模型可写成如下形式:

 

式中c(x) ,ceq(x)为非线性向量函数。

Matlab中的命令是：

[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

例：求下列非线性规划：

 用matlab编制代码如下：

function f = fun1(x);
f = sum(x.^2)+8;
function [g,h] = fun2(x);
g = [-x(1)^2+x(2)-x(3)^2
     x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
h = [-x(1)-x(2)^2+2
     x(2)+2*x(3)^2-3]; %非线性等式约束
[x,y] = fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')

结果如下：

x1 = 0.5522；x2 = 1.2033；x3 = 0.9478；

最小值y = 10.6511。