Track to Detect and Segment: An Online Multi-Object Tracker

论文与代码地址：链接

介绍和相关工作

TraDeS 延续JDT的思想，但是和一般的JDT不同的是，他利用追踪获得的信息来反馈检测，从而更好的进行追踪，不同范式对比如下图：

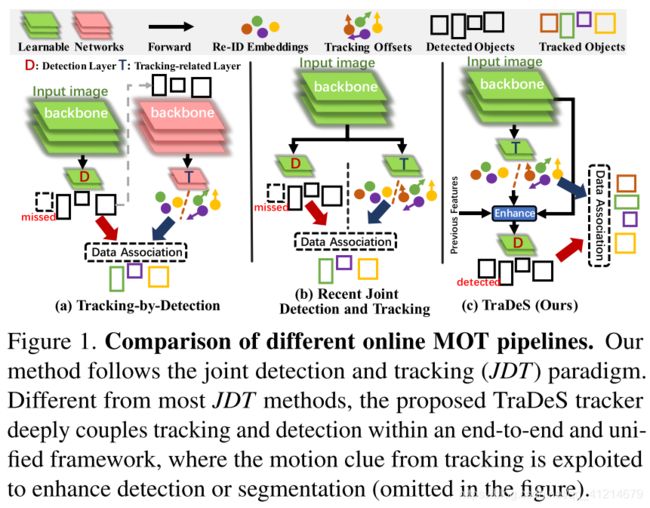
对比DBT范式的两个backbone，JDT范式有天然的优势，一个网络同时实现检测和关联任务，能更加快速的进行推理。

但是JDT虽然网络共享，良好的检测对于追踪的稳定和一致是有益的，但是相较于追踪后的结果，检测仍然是独立的，也就是追踪后得到的结果对下次检测几乎无任何关系。并且其中使用的re-ID损失往往不利于检测效果的提升，re-ID的损失关注的是类内的变量，需要尽可能的将类内拉开，而检测的目的是最大化类间的区别，最小化类内的变量。

面对以上问题，作者认为使用追踪的线索应该来帮助检测，并且在模型中考虑了类间变量，在学习有效embedding的同时，适应检测损失。基于以上两点提出了TraDeS模型，类似于CenterNet，模型中的特征图中的每个点代表一个目标中心或者背景区域，通过将追踪整合进检测的同时，专门设计了一个re-ID学习机制来解决问题。

相应的作者提出了两个模块：
1.基于代价度量的关联模块（a cost volume based association (CVA) module）；
2.运动指导的特征整理模块（a motion-guided feature warper (MFW) module）。

CVA模块通过backbone提取点级re-ID embedding特征来构建一个存储两帧间的所有embedding对之间的匹配相似度的代价向量（cost volume）。利用代价度量，推理出追踪的偏移（所有点的时空位移，如潜在目标的中心点在两帧中位移）。这些追踪偏移加上提取的embedding一起构建数据关联。

MFW利用追踪偏移作为运动线索，用来传播和增强目标特征。最终传播的特征和当前的特征一起聚集来实现检测和分割。

如下图所示，追踪偏移是参考外貌embedding相似度进行预测的，因此模型可以在大规模运动或者低帧情况下匹配目标（图3），也可以在不同数据集中实现精准追踪。

有之前的工作尝试过使用追踪的结果来为原始检测得分赋权，虽然利用了追踪信息，但是还是存在缺点：

1. 追踪只在检测后处理（检测结果已经出了，只影响其得分）起作用，检测和追踪任然单独优化，这样追踪器的效果任然依赖于检测器。
2. 手动重新赋权的机制需要对具体检测器和追踪器进行人工微调。

和之前工作相比，TraDeS 的检测器利用追踪器的结果进行额外学习，且不需要复杂的赋权机制，检测性能更加鲁棒。

代价度量（Cost Volume.）之前也已经被成功运用到了两帧之间关联像素的深度评估或者光流评估，这里引用到MOT进行学习re-ID embedding和推导追踪偏移。

TraDeS Tracker

TraDeS基于基于点的检测器进行构建的，CenterNet输入图片$I$尺寸为$R^{H\times W\times 3}$，通过backbone网络$\varphi (\cdot )$获得特征基础特征$f=\varphi (I)$.，$f\in R^{H_F\times W_F\times 64}，H_F=H/4，W_F=W/4$。一系列头卷积分支利用$f$构建类级别中心热度图（center heatmap）$P\in R^{H_F\times W_F\times N_{cls}}$和具体任务预测图（2D目标获得3D目标）。$N_{cls}$表示类别数，
CenterNet通过中心点（峰点$P$）和在该点处相应的具体任务预测进行目标检测。

在CenterNet基础上增加额外的头来预测追踪偏移映射$O^B\in R^{H_F\times W_F\times 2}$用于数据关联,$O^B$用于计算所有点的在帧$t$对应于过去帧$t-\tau$的时空位移。

TraDeS 模型如下：

基于代价度量的关联模块

代价度量：

从两张原图$I^t$和$I^{t-\tau }$获得两个基础特征图$f^t$和$f^{t-\tau }$。通过embedding网络$\sigma (\cdot )$提取相应的re-ID embedding：${\mathbf{e}}^t=\sigma \left({\mathbf{f}}^t\right)\in {\mathbb{R}}^{H_F\times W_F\times 128}$。用这两个提取的embedding来构建存储当前帧点到过去帧相应点的密集相似度的代价度量。

具体计算首先通过对embedding进行倍率为2的下采样，获得$e^{\prime }\in {\mathbb{R}}^{H_C\times W_C\times 128}$，其中$H_C=H_F/2,W_C=W_F/2$。对于从两张图获得的$e^{\prime t}$和$e^{\prime t-\tau }$，通过矩阵乘法或者4维的代价度量$C\in {\mathbb{R}}^{H_C\times W_C\times H_C\times W_C}$:$$C_{i,j,k,l}={\mathbf{e}}_{i,j}^t{\mathbf{e}}_{k,l}^{\prime t-\tau \top }\text{\hspace{1em}(1)}$$
$C_{i,j,k,l}$表示$t$帧中点$(i,j)$和$t-\tau$帧中点$(k,l)$的embedding相似度，其中$f$和$e^{\prime }$中每个点表示一个实体。

追踪偏移：

基于代价度量$C$，计算追踪偏移矩阵$O\in {\mathbb{R}}^{H_C\times W_C\times 2}$，用以表示两帧之间相应点之间的时空位移。

简要介绍$O_{i,j}\in {\mathbb{R}}^2$的估计过程：
如上图2模型中所示，对于一个目标$x$，中心点在$t$帧中为$(i,j)$，可以从代价度量矩阵中获得他的相应点的2维代价度量图：${\mathbf{C}}_{i,j}\in {\mathbb{R}}^{H_C\times W_C}$。${\mathbf{C}}_{i,j}$保存$x$和其他$t-\tau$中所有点的匹配相似度。

然后使用${\mathbf{C}}_{i,j}$进行$O_{i,j}\in {\mathbb{R}}^2$的估计：第一步： ${\mathbf{C}}_{i,j}$分别通过$H_C\times 1$和$1\times W_C$两个核进行最大池化，然后分别通过softmax进行标准化，获得${\mathbf{C}}_{i,j}^W\in [0,1{]}^{1\times W_C}$和${\mathbf{C}}_{i,j}^H\in [0,1{]}^{H_C\times 1}$。其中${\mathbf{C}}_{i,j}^W$和${\mathbf{C}}_{i,j}^H$组成目标$x$出现在t − τ帧上指定的水平和垂直位置的概率。比如${\mathbf{C}}_{i,j,l}^W$表示目标$x$出现在t − τ帧上位置$(\ast ,l)$的概率。第二步 ：已经获得了${\mathbf{C}}_{i,j}^W$和${\mathbf{C}}_{i,j}^H$，即以及获得了到t − τ具体位置的概率。重新定义两个水平和垂直方向的偏移属性，分别表示$x$出现在这些位置的真实偏移值，${\mathbf{M}}_{i,j}\in {\mathbb{R}}^{1\times W_C}$和${\mathbf{V}}_{i,j}\in {\mathbb{R}}^{H_C\times 1}$表示水平和垂直偏移属性：
$$\{\begin{array}{ll}{M}_{i,j,l}=(l-j)\times s& 1\le l\le W_C\\ V_{i,j,k}=(k-i)\times s& 1\le k\le H_C\end{array}\text{\hspace{1em}(2)}$$
$s$表示特征图$e^{\prime }$较于原图的缩放倍数，实验中改为8。$M_{i,j,l}$表示$x$出现在t − τ中位置$(\ast ,l)$的水平偏移。最终的追踪偏移通过可能性矩阵和偏移矩阵的点积推导：$${\mathbf{O}}_{i,j}={\left[{\mathbf{C}}_{i,j}^{H\top }{\mathbf{V}}_{i,j},{\mathbf{C}}_{i,j}^W{\mathbf{M}}_{i,j}^{\top }\right]}^{\top }\text{\hspace{1em}(3)}$$
轨迹偏移矩阵$\mathbf{O}$大小为$H_C\times W_C$，每个元素包含两个量，$\mathbf{O}\in {\mathbb{R}}^{H_C\times W_C\times 2}$。将其通过倍率为2的下采样，获得${\mathbf{O}}^C\in {\mathbb{R}}^{H_F\times W_F\times 2}$，用于MFW的运动线索以及后续的数据关联。

训练：

$\sigma (\cdot )$是CVA中唯一可学习的部分，训练的目标是学习到有效的embedding $e$。为了实现对$e$的监督，但是不直接使用re-ID损失对$e$监督，而是去监督代价度量。首先当在$t$帧的位置$(i,j)$的目标在$t-\tau$帧的$(k,l)$出现则定义$Y_{ijkl}=1$，否则定义$Y_{ijkl}=0$。然后使用focal loss的形式计算CVA逻辑回归训练损失：
$$L_{CVA}=\frac{-1}{{\sum }_{ijkl}{Y}_{ijkl}}\sum _{ijkl}\{\begin{array}{cl}{\alpha }_1\log \left(C_{i,j,l}^W\right)+{\alpha }_2\log \left(C_{i,j,k}^H\right)& \text{ if }{Y}_{ijkl}=1\\ & \\ 0& \text{ otherwise }\end{array}\text{\hspace{1em}(4)}$$
其中${\alpha }_1=(1-C_{i,j,l}^W{)}^{\beta }$，${\alpha }_2=(1-C_{i,j,k}^H{)}^{\beta }$，$\beta$是focal loss的超参。${\mathbf{C}}_{i,j,l}^W$和${\mathbf{C}}_{i,j,k}^H$已经由softmax计算得出，不仅会存在$(i,j)$和$(k,l)$的相似度，也包含了$(i,j)$和其他所有点的相似度信息。通过如此优化，不仅强制一个对象不仅在前一个框架中接近自己，而且排斥其他对象和背景区域。

下面会有实验证明这种损失的有效性，如图3和图6所示，该模块定义的轨迹偏移可以在低帧或者一些列运动场景下有很强的鲁棒。

运动指导的特征整理模块

MFW模块的目的是利用预测的轨迹偏移$O^C$作为运动线索来调整和传播$f_{t-\tau }$到当前帧，以便弥补和增强$f_t$。通过一个可变性卷积实现有效的时序传播，通过聚集传播来的特征从而增强$f_t$。

时序传播：
可变性卷积（DCN）通过一个时空偏移图和一个过去的特征图作为输入，输出一个传播特征。时空偏移图${\mathbf{O}}^D\in {\mathbb{R}}^{H_F\times W_F\times 2K^2}$使用从CVA模块获得的$O^C$通过3 × 3卷积$\gamma (\cdot )$获得，$K=3$为DCN的核宽和高。也可以将$f^t-f^{t-\tau }$获得的参差特征送入$\gamma (\cdot )$作为额外的运动线索。

由于主要是基于中心点的检测和分割，所以不直接调整$f^{t-\tau }$，而是通过热度图来给他一个中心的注意力获得最终的前一帧特征${\bar{f}}^{t-\tau }\in {\mathbb{R}}^{H_F\times W_F\times 64}$：$${\overline{\mathbf{f}}}_q^{t-\tau }={\mathbf{f}}_q^{t-\tau }\circ {\mathbf{P}}_{agn}^{t-\tau },q=1,2,\dots ,64\text{\hspace{1em}(5)}$$
$q$是通道索引，$◦$是哈德曼乘积。${\mathbf{P}}_{agn}^{t-\tau }\in {\mathbb{R}}^{H_F\times W_F\times 1}$是从$P^{t-\tau }$（开头由CenterNet计算得到的）获得的不可知类的中心热度图。

获得了$O^D$和${\bar{f}}^{t-\tau }$，通过DCN获得最终的传播模特征：$${\hat{\mathbf{f}}}^{t-\tau }=DCN\left({\mathbf{O}}^D,{\overline{\mathbf{f}}}^{t-\tau }\right)\in {\mathbb{R}}^{H_F\times W_F\times 64}$$

特征增强：

通过${\hat{\mathbf{f}}}^{t-\tau }$来增强$f^t$对遮挡模糊等负面效果的抵抗获得特征${\tilde{\mathbf{f}}}_q^t$：
$${\tilde{\mathbf{f}}}_q^t={\mathbf{w}}^t\circ {\mathbf{f}}_q^t+\sum _{\tau =1}^T{\mathbf{w}}^{t-\tau }\circ {\hat{\mathbf{f}}}_q^{t-\tau },q=1,2,\dots ,64\text{\hspace{1em}(6)}$$
${\mathbf{w}}^t\in {\mathbb{R}}^{H_F\times W_F\times 1}$是$t$帧的自适应权重，${\sum }_{\tau =0}^T{\mathbf{w}}_{i,j}^{t-\tau }=1$。$T$为用于聚合的过去特征的数目。$w$由两个卷积加一个softmax函数获得，实验中赋权比平均效果要好。

加强后的特征${\tilde{\mathbf{f}}}_q^t$送入头网络生成当前帧检测框或者masks。实验证明有效减少FN和修复消失目标的tracklet。

Tracklet的生成

总体结构如图2，基于${\tilde{\mathbf{f}}}_q^t$通过三个不同的头网络分别获得不同任务检测结果，对于检测使用CenterNet，对于分割，使用基于点的CondInst。

给定位置$(i,j)$的检测，执行两轮数据关联：
DA-Round (i) ：首先在$t-1$帧上坐标$(i,j)+O_{i,j}^C$且半径$r$（所有检测框宽高的均值）内，先将他和最近的未匹配的检测关联，$O_{i,j}^C$指标是$I^t$和$I^{t-1}$之间的轨迹偏移。

DA-Round (ii)：如果该位置检测在第一轮未匹配上，则计算他的embedding和其余未匹配或历史中断的tracklets的embedding余弦相似度，将检测分配给相似度得分最高且需大于阈值（0.3）的轨迹。如果还未匹配，则作为新轨迹。

TraDeS Loss:$$L=L_{CVA}+L_{det}+L_{mask}$$其中$L_{det}$为CenterNet的2D,3D检测损失，$L_{mask}$实例分割损失。

实验

消融实验：

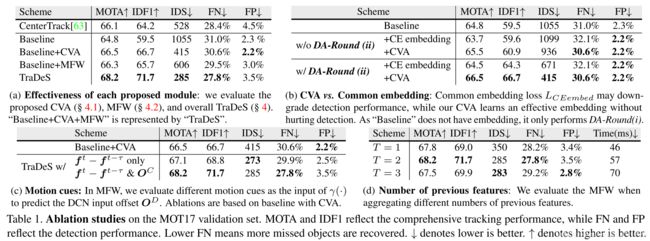
MOT Challenge 2D追踪数据集实验：

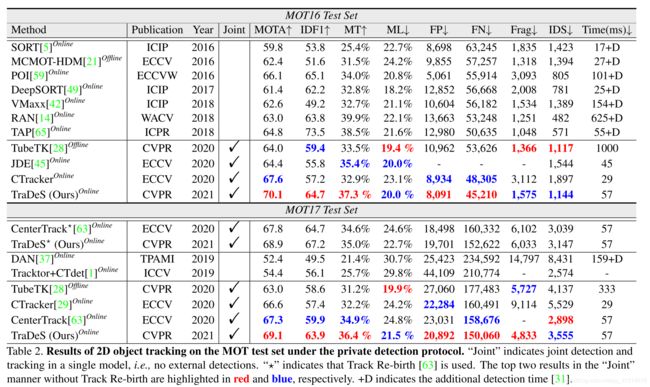
nuScenes数据集3D目标追踪实验：

MOTS实例分割实验：

YouTube-VIS验证集实例分割：

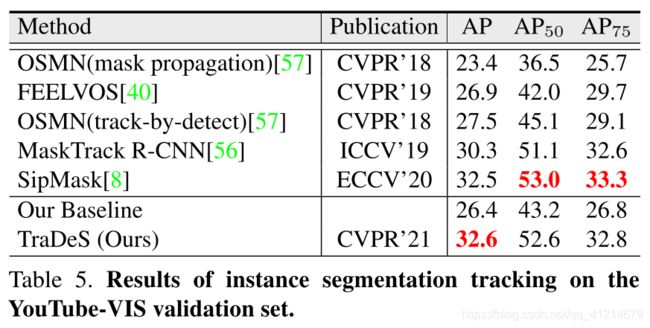
总结

一个新颖的JDT模型，集中使用追踪信息来回馈检测，使用位置轨迹偏移信息更好指导检测。主要的两个模块CVA 和MFW，CVA负责学习re-ID的embedding以及为运动建模一个4维的代价度量；MFW从CVA接受运动信息，从而传播过去的目标特征图，增强当前帧特征图进行检测或者分割。