数学建模与数据分析 || 3. 面向数据的特征提取方法: 探索性数据分析

面向数据的特征提取方法: 探索性数据分析

一般情况下, 原始数据(又称粗数据, 存在缺失、异常、无关特征多等特点)是无法直接应用于模型进行数据分析的, 因为模型强烈依赖于相关性. 这种数据需要进行特征提取,将数据的列进行修正, 生成具有相关性的列.

特征提取的方法有两种, 一种是面向数据的探索性数据分析; 另一种是面向模型的特征提取方法, 如岭回归的正则化方法.

本节将通过一个例子详细介绍第一种方法, 利用探索性分析方法对原始数据进行加工,以适应模型.

1. 原始数据的准备

数据的准备工作包括数据的读取、格式转换、相关性展示等. 本部分所需要的数据可通过如下链接进行下载

链接: https://pan.baidu.com/s/1t2CSFluDXVvFjPUNiBz0xg 提取码: 9gjk

1.1 导入 python 模块

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('fivethirtyeight')
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

1.2 导入数据集并进行宏观认识

data=pd.read_csv('data/DieTanic_train.csv')
data.head()

data.columns

Index([‘PassengerId’, ‘Survived’, ‘Pclass’, ‘Name’, ‘Sex’, ‘Age’, ‘SibSp’,
‘Parch’, ‘Ticket’, ‘Fare’, ‘Cabin’, ‘Embarked’],
dtype=‘object’)

1.3 数据集描述

题目提供的训练数据集包含11个特征，分别是：

• Survived:0代表死亡，1代表存活
• Pclass:乘客所持票类，有三种值(1,2,3)
• Name:乘客姓名
• Sex:乘客性别
• Age:乘客年龄(有缺失)
• SibSp:乘客兄弟姐妹/配偶的个数(整数值)
• Parch:乘客父母/孩子的个数(整数值)
• Ticket:票号(字符串)
• Fare:乘客所持票的价格(浮点数，0-500不等)
• Cabin:乘客所在船舱(有缺失)
• Embark:乘客登船港口:S、C、Q(有缺失)

2. 数据的预处理

对数据的预处理是非常有必要的, 无论进行机器学习还是深度学习都需要符合要求的特定格式的输入. 预处理手段包括缺失数据的填补、异常数据的删除、数据的归一化、数据格式的转换、类别的规模是否均衡等等.

2.1 缺失数据的甄别

data.isnull().sum() #checking for total null values

PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64

2.2 类别规模的评估

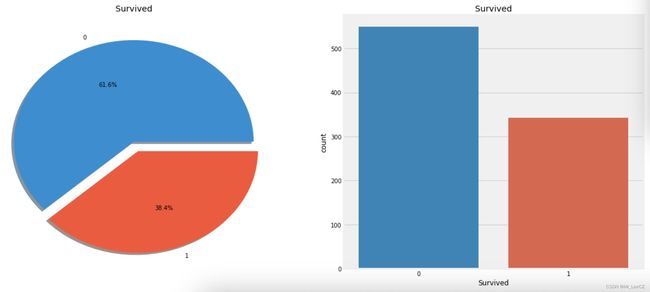
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
sns.countplot('Survived',data=data,ax=ax[1])
ax[1].set_title('Survived')
plt.show()

训练集 891 名乘客中只有大约 350 人幸存，占比 38.4%. 两个类别的规模相差不悬殊, 可以进行正常分类. 下一步,我们需要继续深挖以获取更有用的信息，了解哪些人的生存几率更大, 哪些因素会影响生存几率。我们试图通过分析数据集的不同特征确定生存机率，这些特征包括 Sex, Port Of Embarcation, Age 等.

3. 数据特征的处理

此数据中包含三种类型的数据类型:

• 范畴特征：Sex,Embarked.
  一种变量是有两个或者两个以上的分组，如性别变量。这类变量无法进行排序，称为定类变量。
• 序数特征: PClass
  序数特征与范畴特征类似，不同的是它有排序的意义。例如，身高的高、中、矮，称为序数特征。这类特征可以进行相对排序。
• 连续特征：Age
  特征的值可视为连续性随机变量

3.1 第一个因变量- 分析范畴特征：Sex

data.groupby(['Sex','Survived'])['Survived'].count()

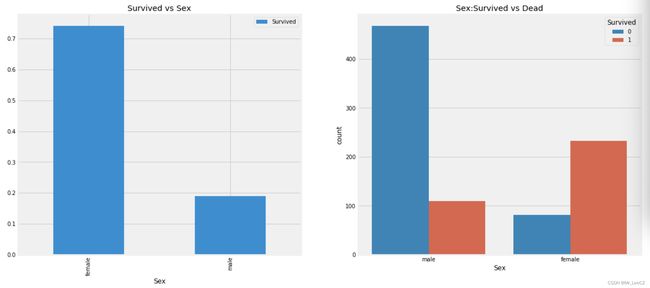
f,ax=plt.subplots(1,2,figsize=(18,8))
data[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
sns.countplot('Sex',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Sex:Survived vs Dead')
plt.show()

这看起来很有趣。船上的男性人数远远多于女性人数。然而，女性获救人数几乎是男性获救人数的两倍。女性在船上的存活率约为75%，而男性约为18-19%。

这个特征似乎是一个比较重要的特征，为了确定其重要程度，还需要分析一下其它特征

3.2 定序特征分析：Pclass

pd.crosstab(data.Pclass,data.Survived,margins=True).style.background_gradient(cmap='summer_r')

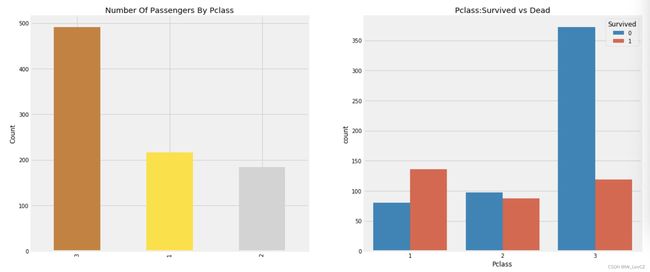
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Pclass'].value_counts().plot.bar(color=['#CD7F32','#FFDF00','#D3D3D3'],ax=ax[0])
ax[0].set_title('Number Of Passengers By Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Pclass:Survived vs Dead')
plt.show()

我们可以清楚地看到，Pclass 1的Passenegers在救援时被给予了非常高的优先级。尽管乘坐Pclass 3的乘客数量要高得多，但幸存的人数占比却非常低，大约在25%左右。

Pclass 1 的存活率大约63%，而Pclass2的存活了大约48%，Pclass 3的存活率大约在25%左右，这个因素的差异可视为影响存活率的一个重要因素

让我们再深入一点，看看其他有趣的观察结果。让我们一起用 sex 和 Pclass 来检查存活率。

pd.crosstab([data.Sex,data.Survived],data.Pclass,margins=True).style.background_gradient(cmap='summer_r')

3.3 连续性特征：Age

3.3.1 缺失数据特征的宏观认识

print('Oldest Passenger was of:',data['Age'].max(),'Years')
print('Youngest Passenger was of:',data['Age'].min(),'Years')
print('Average Age on the ship:',data['Age'].mean(),'Years')

Oldest Passenger was of: 80.0 Years
Youngest Passenger was of: 0.42 Years
Average Age on the ship: 29.69911764705882 Years

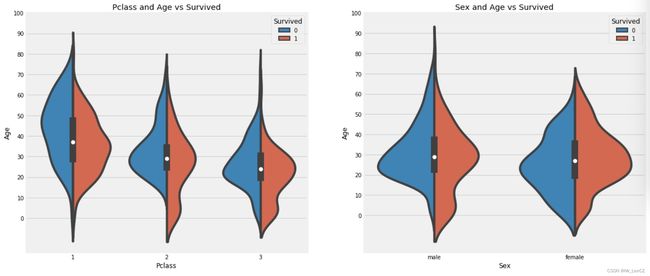
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=data,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=data,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()

3.3.2 缺失数据特征的填充

• 提取名字中的称谓信息

data['Initial']=0
for i in data:
    data['Initial']=data.Name.str.extract('([A-Za-z]+)\.') # 抽取致意用语

这里我们使用正则表达式[A-Za-z]+).它所做的是，它寻找在a-z或a-z之间的字符串，后面跟着分割号“点”，这样我们就成功地从名字中提取出了名字中的称谓。

pd.crosstab(data.Initial,data.Sex).T.style.background_gradient(cmap='summer_r') #Checking the Initials with the Sex

有一些拼写错误的首字母，如Mlle或Mme，它们代表的是Miss。我将把它们替换为Miss，其他的值也一样。

data['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr'],inplace=True)

data.groupby('Initial')['Age'].mean() #lets check the average age by Initials

• 填充年龄的缺失值

## Assigning the NaN Values with the Ceil values of the mean ages
data.loc[(data.Age.isnull())&(data.Initial=='Mr'),'Age']=33
data.loc[(data.Age.isnull())&(data.Initial=='Mrs'),'Age']=36
data.loc[(data.Age.isnull())&(data.Initial=='Master'),'Age']=5
data.loc[(data.Age.isnull())&(data.Initial=='Miss'),'Age']=22
data.loc[(data.Age.isnull())&(data.Initial=='Other'),'Age']=46

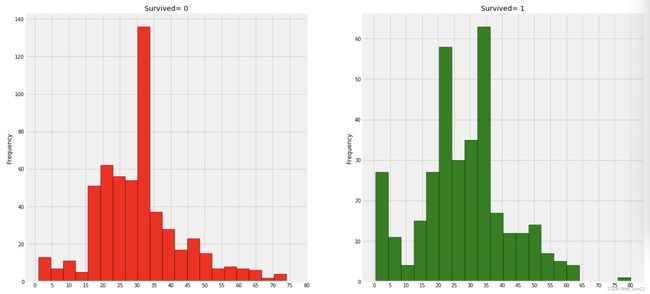
f,ax=plt.subplots(1,2,figsize=(20,10))
data[data['Survived']==0].Age.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('Survived= 0')
x1=list(range(0,85,5))
ax[0].set_xticks(x1)
data[data['Survived']==1].Age.plot.hist(ax=ax[1],color='green',bins=20,edgecolor='black')
ax[1].set_title('Survived= 1')
x2=list(range(0,85,5))
ax[1].set_xticks(x2)
plt.show()

3.4 范畴特征：Embarked

pd.crosstab([data.Embarked,data.Pclass],[data.Sex,data.Survived],margins=True).style.background_gradient(cmap='summer_r')

3.5 对因素 Embarked 的空缺值进行填充

我们看到大多数乘客从S港登机，我们将NaN替换为S港。

data['Embarked'].fillna('S',inplace=True)

4. 特征工程

特征之间的相关性, 特征之间既不能存在强相关性,同时也不能不相关.

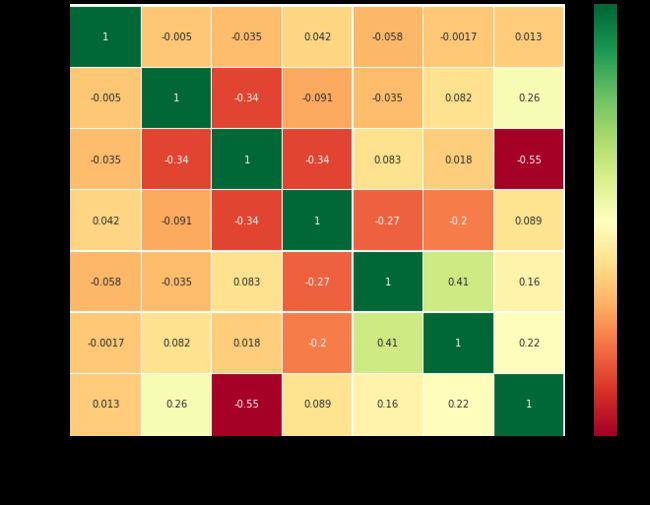
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2) #data.corr()-->correlation matrix
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()

各特征之间出现浅绿色为最佳, 深绿则是强相关, 暖色则是负相关.

4.1 热力图的解释

首先要注意的是，只比较数字特性，因为很明显，我们不能在字母或字符串之间关联。在理解这幅图之前，让我们先看看到底什么是相关性。

正相关:如果特征A的增加导致特征B的增加，则两者正相关。值1表示完全正相关。

负相关:如果特征A的增加导致特征B的减少，则两者是负相关的。值-1表示完全负相关。

现在我们假设两个特征高度或完全相关，一个特征的增加会导致另一个特征的增加。这意味着这两个特征都包含高度相似的信息，而信息的差异非常小或没有。这被称为多线性，因为它们包含几乎相同的信息。

你认为我们应该同时使用它们吗，因为其中一个是多余的。在建立或训练模型时，我们应该尽量消除冗余特征，因为它减少了训练时间和许多这样的优点。

现在从上面的热图中，我们可以看到这些特征并不是很相关。SibSp与Parch i的相关性最高，0.41。所以我们需要继续处理特征

4.2 特征工程和数据清洗

什么叫特征工程?

当我们得到一个具有特征的数据集时，并不是所有的特征都是重要的。可能有许多冗余的特性应该被消除。我们还可以通过观察或从其他特征中提取信息来获得或添加新的特征。

例如，使用Name特性获取初始化特性。让我们看看我们是否可以得到任何新的功能，并删除一些。同时，我们也会将现有的相关特征转化为适合的形式进行预测建模。

4.2.1 增加一个新的特征：Age_band

年龄特征的问题:

前面提到的年龄特征是一个连续性特征, 年龄特征作为一个连续型特征用于机器学习是有问题的。

例如:如果我说按性别分组或安排运动员，我们可以很容易地将他们按男性和女性分开。

如果我说按年龄分组，你会怎么做?如果有30个人，则可能有30个年龄值。这是有问题的。

我们需要将这些连续的值转换成分类的值，或者通过封边，或者通过标准化。我将使用binning I。把不同年龄的人分组到一个箱子里，或者给他们分配一个值。

乘客的最大年龄是80岁。所以我们把0-80的范围分成5个部分。所以80/5 = 16。箱子的大小是16。

data['Age_band']=0
data.loc[data['Age']<=16,'Age_band']=0
data.loc[(data['Age']>16)&(data['Age']<=32),'Age_band']=1
data.loc[(data['Age']>32)&(data['Age']<=48),'Age_band']=2
data.loc[(data['Age']>48)&(data['Age']<=64),'Age_band']=3
data.loc[data['Age']>64,'Age_band']=4

4.2.2 增加新特征：Family_Size and Alone

现在，我们可以创建一个名为“Family_size”和“Alone”的新功能，并对其进行分析。这个特性是Parch和SibSp的总和。它给了我们一个综合数据，这样我们就可以检查存活率是否与乘客的家庭规模有关。表示乘客是否独处。

data['Family_Size']=0
data['Family_Size']=data['Parch']+data['SibSp']#family size
data['Alone']=0
data.loc[data.Family_Size==0,'Alone']=1#Alone

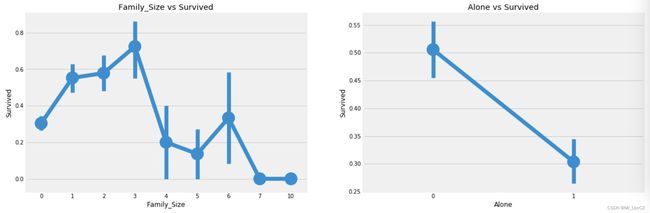
f,ax=plt.subplots(1,2,figsize=(18,6))
sns.factorplot('Family_Size','Survived',data=data,ax=ax[0])
ax[0].set_title('Family_Size vs Survived')
sns.factorplot('Alone','Survived',data=data,ax=ax[1])
ax[1].set_title('Alone vs Survived')
plt.close(2)
plt.close(3)
plt.show()

4.2.3 增加新的特征：Fare_Range

由于票价也是一个连续的特征，我们需要将其转换为有序值。为此我们将使用pandas.qcut。

所以qcut所做的就是根据我们通过的容器的数量来分割或排列值。所以如果我们传递5个箱子，它会将这些值等间隔地排列成5个独立的箱子或值范围。

data['Fare_Range']=pd.qcut(data['Fare'],4)
data.groupby(['Fare_Range'])['Survived'].mean().to_frame().style.background_gradient(cmap='summer_r')

data['Fare_cat']=0
data.loc[data['Fare']<=7.91,'Fare_cat']=0
data.loc[(data['Fare']>7.91)&(data['Fare']<=14.454),'Fare_cat']=1
data.loc[(data['Fare']>14.454)&(data['Fare']<=31),'Fare_cat']=2
data.loc[(data['Fare']>31)&(data['Fare']<=513),'Fare_cat']=3

4.2.4 将字符串值转换为数字

因为我们不能将字符串传递给机器学习模型，所以我们需要将特Sex, Embarked 等变换为数字特征

data['Sex'].replace(['male','female'],[0,1],inplace=True)
data['Embarked'].replace(['S','C','Q'],[0,1,2],inplace=True)
data['Initial'].replace(['Mr','Mrs','Miss','Master','Other'],[0,1,2,3,4],inplace=True)

4.2.5 丢弃一些不需要的特征

• Name–> 我们不需要名称特性，因为它不能转换为任何分类值。
• Age–> 我们有Age_band特性，所以不需要它。
• Ticket–> 它是任何不能分类的随机字符串。
• Fare–> 已经有了特征 Fare_cat，因此该特征也不需要了
• Cabin–> 很多NaN值，也有很多乘客有多个舱位。所以这是一个无用的特性
• Fare_Range–> 已经有了特征 Fare_cat，因此该特征也不需要了
• PassengerId–> 与分类无关

data.drop(['Name','Age','Ticket','Fare','Cabin','Fare_Range','PassengerId'],axis=1,inplace=True)
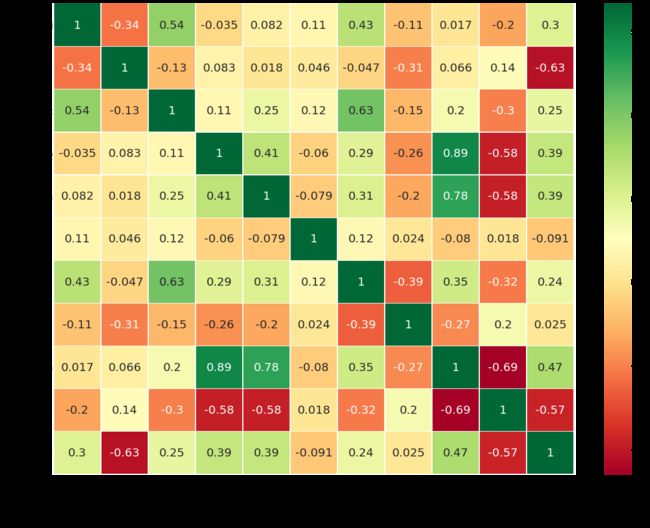
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2,annot_kws={'size':20})
fig=plt.gcf()
fig.set_size_inches(18,15)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()

从上面的相关图中，我们可以看到一些正相关的特征。如SibSp，Family_Size ，Parch ，Family_Size。还有一些负相关特征如 Alone 和 Family_Size

5. 模型的深入理解是获高水平奖项的重要保障

我们从EDA部分获得了一些见解。但这样的话，我们并不能准确地预测或判断一名乘客是生还还是遇难。现在我们将预测乘客是否会幸存使用一些优秀的分类算法。下面是我将使用的算法来制作模型:

1. Logistic Regression
2. Support Vector Machines(Linear and radial)
3. Random Forest
4. K-Nearest Neighbours
5. Naive Bayes
6. Decision Tree

从多元线性回归问题看逻辑回归问题

回归问题是寻找一个或多个自变量(解释变量)与因变量（观测变量）的关系，输入为$x_1,x_2,\cdots ,x_m$与$y$的关系

输入变量$X=\{x_1,x_2,\cdots ,x_m\}$和$y$

假设我们有线性回归回归模型
$$y={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_m{X}_m+ϵ$$
即
$$y=X\beta +\epsilon$$
并且有$n$组数据$(y(i),x_1(i),\dots ,x_m(i){)}_{i=1}^n$.

从机器学习的角度看线性回归问题，是基于损失函数(Loss function)进行建模的

$$S=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

OLS 回归用于计算回归系数 ${\beta }_i$ 的估值 ${\beta }_0,{\beta }_1,\cdots ,{\beta }_n$，使误差平方
$$L(\beta )=\sum _{t=1}^k(y(t)-{\beta }_0-{\beta }_1{X}_1(t)-\cdots -{\beta }_n{X}_n(t){)}^2=||y-X\beta |{|}^2$$
最小化。

$$\frac{\partial L(\beta )}{\partial \beta }=2X^T(y-X\beta )=0$$
即
$$X^{T}y=X^{T}X\beta$$
当$X^{T}X$满秩时，得
$$\beta =(X^{T}X{)}^{-1}{X}^{T}y$$

如果两个因子共线性时，矩阵中的列刚好抵消，矩阵$X^{T}X$是不满秩的，没有逆，此时的解不唯一。

from sklearn.linear_model import LogisticRegression #logistic regression
from sklearn.model_selection import train_test_split

train,test=train_test_split(data,test_size=0.3,random_state=0,stratify=data['Survived'])
train_X=train[train.columns[1:]]
train_Y=train[train.columns[:1]]
test_X=test[test.columns[1:]]
test_Y=test[test.columns[:1]]
X=data[data.columns[1:]]
Y=data['Survived']

model = LogisticRegression()
model.fit(train_X,train_Y)

model.coef_

array([[-0.73433775, 1.99943271, -0.37708714, 0.08199481, 0.11389123,
0.45564992, -0.43677308, -0.29509233, -0.38254696, 0.43878049]])

prediction3=model.predict(test_X)
print(prediction3)

[0 1 0 1 0 1 0 0 1 1 0 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0
0 0 0 0 1 1 0 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 1 1 0 1 0 0 1 0 1 0 0 0 0
0 1 1 0 1 1 0 1 1 1 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0
0 0 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 0 0 1 1 1 1 0 0 1 0 0 0 1
0 1 0 1 0 0 0 0 0 0 0 1 1 0 1 0 1 0 0 1 1 1 0 1 1 1 0 0 0 0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0
0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 1 1 1 1 0 0 0 0 0 1 1 1 0
0 1 1 0 1 0 0 0 0]

from sklearn import metrics

print('The accuracy of the Logistic Regression is',metrics.accuracy_score(prediction3,test_Y))

The accuracy of the Logistic Regression is 0.8171641791044776