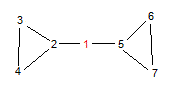并查集【7.13】
文章目录
- 一:引入
- 二:介绍
- 三.具体实现
-
- 1.并查集基础操作:查询
- 2.并查集基础操作:合并
- 3.并查集优化1:路径压缩
- 4.并查集优化2:按秩合并(启发式合并)
- 5.带权并查集(边带权并查集)
- 6.种类并查集(扩展域并查集)
- 四.一堆好题
-
- 1.亲戚(relation)
-
- 题目背景
- 题目描述
- 输入格式
- 输出格式
-
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 思路
- AC代码
-
- 卡常版(用时:35ms;内存:856.00KB)
- 正常版(用时:37ms;内存:812.00KB)
- 2.打击犯罪(black)
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入
- 样例输出
- 数据范围与提示
- 思路
- AC代码
- 3.[NOI2002] 银河英雄传说
-
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 4.[NOI2001] 食物链
-
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 5.格子游戏
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入
- 样例输出
- 思路
- AC代码
- 6.[BOI2003]团伙
-
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 7.P1455 搭配购买
-
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 8.P2814 家谱
-
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 9.犯罪集团
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入
- 样例输出
- 思路
- AC代码
- 10.老旧的桥
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入1
- 样例输出1
- 样例输入2
- 样例输出2
- 样例输入3
- 样例输出3
- 数据范围与提示
- 思路
- AC代码
- 11.造船
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- input
- output
- 数据范围与提示
- 思路
-
-
- 1.子串不为 1 1 1 且 r o o t root root 不为 1 1 1 -- 将子串置为 1 1 1
- 2.子串不为 1 1 1 且 r o o t root root 为 1 1 1 -- 将子串置为 1 1 1
- 3.子串为 1 1 1 且 r o o t root root 不为 1 1 1 -- 将 r o o t root root 置为 1 1 1
- 4.子串为 1 1 1 且 r o o t root root 为 1 1 1 -- 将 r o o t root root 置为 1 1 1
- 1.子串不为 1 1 1 -- 子串置为 1 1 1
- 2.子串为 1 1 1 -- r o o t root root 异或等于 1 1 1
-
- AC代码
- 12.[NOIP2010 提高组] 关押罪犯
-
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 13.明辨是非
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入
- 样例输出
- 数据范围与提示
- 思路
- AC代码
- 14.箱子
-
- 题目描述
- 输入格式
- 输出格式
- 样例
-
- 样例输入
- 样例输出
- 思路
- AC代码
- 15.[NOI2015] 程序自动分析
-
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
-
- 样例输入 #1
- 样例输出 #1
- 样例 #2
-
- 样例输入 #2
- 样例输出 #2
- 提示
- 思路
- AC代码
一:引入
在近几年的国赛(即NOI)中, n ≤ 1 0 8 , 1 0 9 n\leq 10^8,10^9 n≤108,109等大数据频繁出现,所以,这时我们就要引入一种新的数据结构——并查集
二:介绍
并查集( D i s j o i n t − S e t Disjoint-Set Disjoint−Set o r or or U n i o n − F i n d Union-Find Union−Find S e t Set Set)是一种表示不相交集合的数据结构,用于处理不相交集合的合并与查询问题。在不相交集合中,每个集合通过代表来区分,代表是集合中的某个成员,能够起到唯一标识该集合的作用。一般来说,选择哪一个元素作为代表是无关紧要的,关键是在进行查找操作时,得到的答案是一致的(通常把并查集数据结构构造成树形结构,根节点即为代表)。
在不相交集合上,需要经常进行如下操作:
F i n d S e t ( x ) FindSet(x) FindSet(x):查找元素 x x x属于哪个集合,如果 x x x 属于某一集合,则返回该集合的代表。
U n i o n S e t ( x , y ) UnionSet(x,y) UnionSet(x,y):如果元素 x x x 和元素 y y y 分别属于不同的集合,则将两个集合合并,否则不做操作。
并查集的实现方法是使用有根树来表示集合——树中的每个结点都表示集合的一个元素,每棵树表示一个集合,每棵树的根结点作为该集合的代表。
我相信你跟我一样,根本看不懂,那就让我来举个例子
有一所中学内有 28 28 28个班,比如 1 1 1班,我们不可能选择一个没有代表性的人来代表整个班,所以这时,我们用班主任 h e a d 1 head_1 head1代表整个班,再比如 2 2 2班,同样的,班主任 h e a d 2 head_2 head2也可以代表整个班
三.具体实现
1.并查集基础操作:查询
查询操作是递归查询,在查询某个结点在哪一个集合中时,需沿着其父结点,递归向上,因所属集合代表指向的仍然是其本身,所以可以以 f a t h e r [ x ] = x father[x] = x father[x]=x作为递归查询出口。
int FindSet(int x) {
if (father[x] == x) return x;
else return FindSet(father[x]);
}
F i n d S e t FindSet FindSet :如果知道一班有一个人叫 s t u 1 stu_1 stu1,那么我们可以利用他的爸爸们(比如: g r o u p 1 , m o n i t o r 1 group_1,monitor_1 group1,monitor1)来找到他的祖先— h e a d 1 head_1 head1(注:祖先就是他爸爸的爸爸(此处省略 n n n个爸爸 1 ≤ n 1 \leq n 1≤n))
2.并查集基础操作:合并
在进行集合的合并时,只需将两个集合的代表进行连接即可,即一个代表作为另一个代表的父结点。
void UnionSet(int x, int y) {
father[FindSet(x)] = FindSet(y);
}
U n i o n S e t ( x , y ) UnionSet(x,y) UnionSet(x,y):如果想合并1班和2班只需要让班主任 h e a d 2 head_2 head2成为班主任 h e a d 1 head_1 head1的爸爸或者让班主任 h e a d 2 head_2 head2成为班主任 h e a d 1 head_1 head1的儿子
3.并查集优化1:路径压缩
普通的查找实在是太慢,所以,我们得好好想想(用脑袋想不出来时,可以用脚趾敲敲代码,利用 m o n k e y monkey monkey定理打出正确代码 )
发生原因:在合并过程中,可能会形成一条长长的链,随着链越来越长,我们想要从底部找到根结点会变得越来越难。
方法:路径压缩:对于一个集合中的结点,只需要关心它的根结点是谁,不必知道各结点之间的关系(对树的形态不关心),希望每个元素到根结点的路径尽可能短,最好只需要一步。把一条链变成一棵又矮又胖的树,极大地提高了查询效率。
int FindSet(int x) {
if (father[x] == x) return x;
else return father[x] = FindSet(father[x]);
}
这就好比班主任 h e a d 2 head_2 head2有一个儿子 c h i l d 1 child_1 child1,而 c h i l d 1 child_1 child1又有一个儿子 c c h i l d 1 cchild_1 cchild1,现在,直接让 h e a d 2 head_2 head2的孙子 c c h i l d 1 cchild_1 cchild1变成他的儿子 c h i l d 2 child_2 child2
(辈分乱了,大逆不道啊.
4.并查集优化2:按秩合并(启发式合并)
对于一些毒瘤数据,只有一个优化远远不够,所以,还得用上按秩合并(启发式合并)
//初始化
void MakeSet(int n) {
for (int i = 1; i <= n; i++)
father[i] = i, rank[i] = 1;
}
void UnionSet(int x, int y) {
int a = FindSet(x), b = FindSet(y);
if (a == b) return;
if (rank[a] <= rank[b]) father[a] = b;
else father[b] = a;
if (rank[a] == rank[b]) rank[b]++;
}
想要合并一班和二班,我们就比较哪边班主任的儿子多(注:此处的儿子指该班上的人),就让另一个班的班主任 h e a d 1 head_1 head1变成 h e a d 2 head_2 head2的儿子
5.带权并查集(边带权并查集)
在有了路径压缩后,一条链变成了一棵又矮又胖的树,失去了他原来父亲与儿子间的关系.
那么,当我们遇到银河英雄传说与箱子时,我们就会悔恨当初为什么要合并,但是还是有补救的办法———我们需要引入2个数组 d e e p i deep_i deepi来表示从 r o o t root root到第 i i i个点的距离, s i z e i size_i sizei来表示从链底到第 i i i个点的点的数量
6.种类并查集(扩展域并查集)
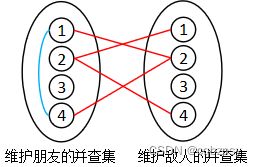
一般的并查集,维护的是具有连通性、传递性的关系,例如亲戚的亲戚是亲戚。但有时候要维护另一种关系:敌人的敌人是朋友(如
食物链和团伙),种类并查集就是为了解决这个问题。
例如下图所示, ( 1 , 2 ) (1, 2) (1,2)是敌人, ( 2 , 4 ) (2, 4) (2,4)是敌人,则 ( 1 , 4 ) (1, 4) (1,4)就是朋友。
四.一堆好题
正所谓大量的练习才能促进进步。
1.亲戚(relation)
P1551 亲戚
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定: x x x 和 y y y 是亲戚, y y y 和 z z z 是亲戚,那么 x x x 和 z z z 也是亲戚。如果 x x x, y y y 是亲戚,那么 x x x 的亲戚都是 y y y 的亲戚, y y y 的亲戚也都是 x x x 的亲戚。
输入格式
第一行:三个整数 n , m , p n,m,p n,m,p,( n , m , p ≤ 5000 n,m,p \le 5000 n,m,p≤5000),分别表示有 n n n 个人, m m m 个亲戚关系,询问 p p p 对亲戚关系。
以下 m m m 行:每行两个数 M i M_i Mi, M j M_j Mj, 1 ≤ M i , M j ≤ N 1 \le M_i,~M_j\le N 1≤Mi, Mj≤N,表示 M i M_i Mi 和 M j M_j Mj 具有亲戚关系。
接下来 p p p 行:每行两个数 P i , P j P_i,P_j Pi,Pj,询问 P i P_i Pi 和 P j P_j Pj 是否具有亲戚关系。
输出格式
p p p 行,每行一个 Yes 或 No。表示第 i i i 个询问的答案为“具有”或“不具有”亲戚关系。
样例 #1
样例输入 #1
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
样例输出 #1
Yes
Yes
No
思路
这是一道模板题 (
这显而易见,解法见正常版代码
AC代码
卡常版(用时:35ms;内存:856.00KB)
#include 正常版(用时:37ms;内存:812.00KB)
#include2.打击犯罪(black)
题目描述
某个地区有 n ( n ≤ 1000 ) n(n≤1000) n(n≤1000)个犯罪团伙,当地警方按照他们的危险程度由高到低给他们编号为 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n,他们有些团伙之间有直接联系,但是任意两个团伙都可以通过直接或间接的方式联系,这样这里就形成了一个庞大的犯罪集团,犯罪集团的危险程度由集团内的犯罪团伙数量唯一确定,而与单个犯罪团伙的危险程度无关(该犯罪集团的危险程度为 n n n)。现在当地警方希望花尽量少的时间(即打击掉尽量少的团伙),使得庞大的犯罪集团分离成若干个较小的集团,并且他们中最大的一个的危险程度不超过 n / 2 n/2 n/2。为达到最好的效果,他们将按顺序打击掉编号 1 1 1到 k k k的犯罪团伙,请编程求出 k k k的最小值。
输入格式
第一行一个正整数 n n n。接下来的 n n n行每行有若干个正整数,第一个整数表示该行除第一个外还有多少个整数,若第 i i i行存在正整数 k k k,表示 i i i, k k k两个团伙可以直接联系。
输出格式
一个正整数,为 k k k的最小值。
样例
样例输入
7
2 2 5
3 1 3 4
2 2 4
2 2 3
3 1 6 7
2 5 7
2 5 6
样例输出
1
数据范围与提示
思路
这道题需要用并查集来维护团伙关系,所以就有了以下这段代码:
for(int i = 1; i <= n; i ++){
int k;
scanf("%d", &k);
for(int j = 1; j <= k; j ++){
int x;
scanf("%d", &x);
int fx = find(x), fy = find(i);
if(fx != fy){
fa[fx] = fy;
size[fy] += size[fx];
if(size[i] > n / 2){
printf("%d\n", i);
return 0;
}
}
}
}
但很可惜,这段代码是错的,为什么。
假设我们让 i i i从 1 1 1到 n n n枚举,便有了如下过程:
[2]—[1]—[5] − > -> −> [3]—[2]—[1]—[5]
那么我们就应该输出 3 3 3
B u t But But, 非常不幸的是,答案是 1 1 1
所以,我们应该倒着推
[7]—[6]—[5] − > -> −> [7]—[6]—[5]—[1]
那么我们应该输出1吗,这样做对吗,如果对,那为什么对?
对的,让我们换组样例:7 2 2 5 3 1 3 4 2 2 4 2 2 3 3 1 6 7 2 5 7 2 5 6这里我们按照思路,应输出 4 4 4.
因为从后向前遍历可以保证之前遍历的点不会与其他点连接,所以第一个找到的答案一定是对的.
故可以得出核心代码:
for (int i = n; i; i--)
for (int j = 1; j <= a[i][0]; j++)
if (a[i][j] > i) {
int fx = find(i), fy = find(a[i][j]);
if (fx != fy) {
fa[fy] = fx;
size[fx] += size[fy];
if (size[i] > n / 2) {
printf("%d\n", i);
return 0;
}
}
}
AC代码
#include 3.[NOI2002] 银河英雄传说
[NOI2002] 银河英雄传说
题目背景
公元 5801 5801 5801 年,地球居民迁至金牛座 α \alpha α 第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历 799 799 799 年,银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。
题目描述
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成 30000 30000 30000 列,每列依次编号为 1 , 2 , … , 30000 1, 2,\ldots ,30000 1,2,…,30000。之后,他把自己的战舰也依次编号为 1 , 2 , … , 30000 1, 2, \ldots , 30000 1,2,…,30000,让第 i i i 号战舰处于第 i i i 列,形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为 M i j,含义为第 i i i 号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第 j j j 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。
然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第 i i i 号战舰与第 j j j 号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
输入格式
第一行有一个整数 T T T( 1 ≤ T ≤ 5 × 1 0 5 1 \le T \le 5 \times 10^5 1≤T≤5×105),表示总共有 T T T 条指令。
以下有 T T T 行,每行有一条指令。指令有两种格式:
-
M i j: i i i 和 j j j 是两个整数( 1 ≤ i , j ≤ 30000 1 \le i,j \le 30000 1≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第 i i i 号战舰与第 j j j 号战舰不在同一列。 -
C i j: i i i 和 j j j 是两个整数( 1 ≤ i , j ≤ 30000 1 \le i,j \le 30000 1≤i,j≤30000),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
依次对输入的每一条指令进行分析和处理:
- 如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息。
- 如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 i i i 号战舰与第 j j j 号战舰之间布置的战舰数目。如果第 i i i 号战舰与第 j j j 号战舰当前不在同一列上,则输出 − 1 -1 −1。
样例 #1
样例输入 #1
4
M 2 3
C 1 2
M 2 4
C 4 2
样例输出 #1
-1
1
提示
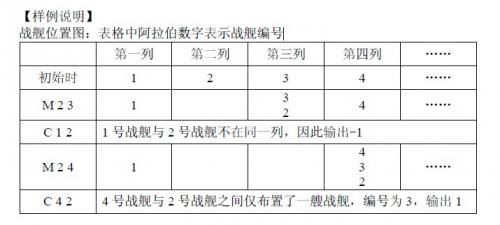
战舰位置图:表格中阿拉伯数字表示战舰编号
思路
经典的带权并查集,具体详见代码
AC代码
#include4.[NOI2001] 食物链
[NOI2001] 食物链
题目描述
动物王国中有三类动物 A , B , C A,B,C A,B,C,这三类动物的食物链构成了有趣的环形。 A A A 吃 B B B, B B B 吃 C C C, C C C 吃 A A A。
现有 N N N 个动物,以 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 编号。每个动物都是 A , B , C A,B,C A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N N N 个动物所构成的食物链关系进行描述:
- 第一种说法是
1 X Y,表示X和Y是同类。 - 第二种说法是
2 X Y,表示X吃Y。
此人对 N N N 个动物,用上述两种说法,一句接一句地说出 K K K 句话,这 K K K 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话
- 当前的话中 X X X 或 Y Y Y 比 N N N 大,就是假话
- 当前的话表示 X X X 吃 X X X,就是假话
你的任务是根据给定的 N N N 和 K K K 句话,输出假话的总数。
输入格式
第一行两个整数, N N N, K K K,表示有 N N N 个动物, K K K 句话。
第二行开始每行一句话(按照题目要求,见样例)
输出格式
一行,一个整数,表示假话的总数。
样例 #1
样例输入 #1
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
样例输出 #1
3
提示
1 ≤ N ≤ 5 ∗ 1 0 4 1 ≤ N ≤ 5 ∗ 10^4 1≤N≤5∗104
1 ≤ K ≤ 1 0 5 1 ≤ K ≤ 10^5 1≤K≤105
思路
经典的种类并查集的好题
先让我列个表格(拿2 1 2举例)
| s e l f self self | f o o d food food | e n e m y enemy enemy |
|---|---|---|
| 1 1 1 | 1 + n 1 + n 1+n | 1 + 2 ∗ n 1 + 2 * n 1+2∗n |
| 2 2 2 | 2 + n 2 + n 2+n | 2 + 2 ∗ n 2 + 2 * n 2+2∗n |
由题 可以知道
2与1 + n是同类, 所以将 f a [ 2 ] fa[2] fa[2]置为 1 + n 1 + n 1+n
同理可得,1 + 2 * n与2 + n,1与2 + 2 * n是同类.
判错只需要判断1和2 + n,1和2是不是同类就可以了
同理我们可以推广出以下表格:
| s e l f self self | f o o d food food | e n e m y enemy enemy |
|---|---|---|
| x x x | x + n x + n x+n | x + 2 ∗ n x + 2 * n x+2∗n |
| y y y | y + n y + n y+n | y + 2 ∗ n y + 2 * n y+2∗n |
可以知道
y与x + n,x + 2 * n与y + n,x与y + 2 * n是同类.
判错只需要判断x和y + n,x和y是不是同类
当样例为
1 1 3时,表格如下:
| s e l f self self | f o o d food food | e n e m y enemy enemy |
|---|---|---|
| 1 1 1 | 1 + n 1 + n 1+n | 1 + 2 ∗ n 1 + 2 * n 1+2∗n |
| 2 2 2 | 2 + n 2 + n 2+n | 2 + 2 ∗ n 2 + 2 * n 2+2∗n |
可以知道
1与2,1 + n与2 + n,1 + 2 * n与2 + 2 * n是同类
所以,当要判断这句话是不是错的,只需要判断1和2 + n,1和2 + 2 * n是不是同类就可以了
同理可推导出
| s e l f self self | f o o d food food | e n e m y enemy enemy |
|---|---|---|
| x x x | x + n x + n x+n | x + 2 ∗ n x + 2 * n x+2∗n |
| y y y | y + n y + n y+n | y + 2 ∗ n y + 2 * n y+2∗n |
可以知道
x与y,x + n与y + n,x + 2 * n与y + 2 * n是同类
判错只需要判断x和y + n,x和y + 2 * n是不是同类就可以了
以上的判错方法其实可以变化 如:
x与y + 2 * n可以变成x + n与y;
其他的就靠你自己推了.
AC代码
#include5.格子游戏
题目描述
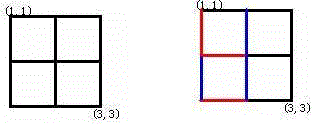
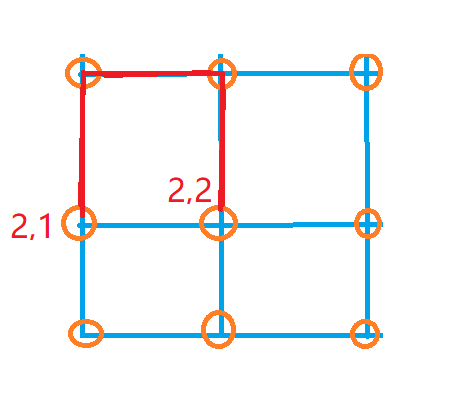
A l i c e Alice Alice和 B o b Bob Bob玩了一个古老的游戏:首先画一个 n × n n × n n×n的点阵(下图 n = 3 n = 3 n=3)
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为 1 1 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了( n ≤ 200 n ≤ 200 n≤200),他们的游戏实在是太长了!他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n n n和 m m m。 m m m表示一共画了 m m m条线。以后 m m m行,每行首先有两个数字( x , y x, y x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是D,则是向下连一条边,如果是R就是向右连一条边。输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。假如 m m m步之后也没有结束,则输出一行 d r a w draw draw
样例
样例输入
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
样例输出
4
思路
本题考察的是并查集的基本用法,上述问题可以转换为:每个点都是一个单独的集合,如果没有构成一个环,就可以在两个集合之间连一条边,如果在一个集合中,那么就代表这两个集合会成环。
一.将每个坐标看成一个点值,为了方便计算,将所有的坐标横纵坐标都减1,第一个位置即(1,1)看成是0,(1,2)看成是1,依次类推,将所有的坐标横纵坐标都减1后,假设当前点是(x,y),该点的映射值是a = (x * n + y),若向下画,则b = [(x + 1) * n + y],若向右画,则b = [x * n + y - 1]。
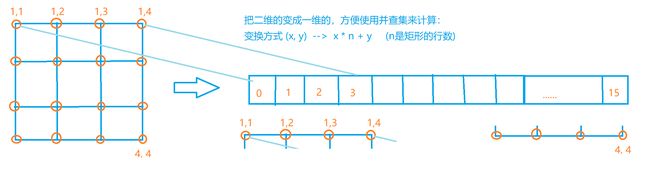
二.枚举所有操作,通过并查集操作判断a和b是否在同一个集合:
1. 若在同一个集合则标记此操作可以让格子形成环
2.若不在同一个集合,则需要将两个集合进行合并
AC代码
#include 6.[BOI2003]团伙
[BOI2003]团伙
题目描述
现在有 n n n 个人,他们之间有两种关系:朋友和敌人。我们知道:
- 一个人的朋友的朋友是朋友
- 一个人的敌人的敌人是朋友
现在要对这些人进行组团。两个人在一个团体内当且仅当这两个人是朋友。请求出这些人中最多可能有的团体数。
输入格式
第一行输入一个整数 n n n 代表人数。
第二行输入一个整数 m m m 表示接下来要列出 m m m 个关系。
接下来 m m m 行,每行一个字符 o p t opt opt 和两个整数 p , q p,q p,q,分别代表关系(朋友或敌人),有关系的两个人之中的第一个人和第二个人。其中 o p t opt opt 有两种可能:
- 如果 o p t opt opt 为
F,则表明 p p p 和 q q q 是朋友。 - 如果 o p t opt opt 为
E,则表明 p p p 和 q q q 是敌人。
输出格式
一行一个整数代表最多的团体数。
样例 #1
样例输入 #1
6
4
E 1 4
F 3 5
F 4 6
E 1 2
样例输出 #1
3
提示
对于 100 % 100\% 100% 的数据, 2 ≤ n ≤ 1000 2 \le n \le 1000 2≤n≤1000, 1 ≤ m ≤ 5000 1 \le m \le 5000 1≤m≤5000, 1 ≤ p , q ≤ n 1 \le p,q \le n 1≤p,q≤n。
思路
类似于
食物链请自行思考
AC代码
#include7.P1455 搭配购买
P1455 搭配购买
题目描述
明天就是母亲节了,电脑组的小朋友们在忙碌的课业之余挖空心思想着该送什么礼物来表达自己的心意呢?听说在某个网站上有卖云朵的,小朋友们决定一同前往去看看这种神奇的商品,这个店里有 n n n 朵云,云朵已经被老板编号为 1 , 2 , 3 , . . . , n 1,2,3,...,n 1,2,3,...,n,并且每朵云都有一个价值,但是商店的老板是个很奇怪的人,他会告诉你一些云朵要搭配起来买才卖,也就是说买一朵云则与这朵云有搭配的云都要买,电脑组的你觉得这礼物实在是太新奇了,但是你的钱是有限的,所以你肯定是想用现有的钱买到尽量多价值的云。
输入格式
第一行输入三个整数, n , m , w n,m,w n,m,w,表示有 n n n 朵云, m m m 个搭配和你现有的钱的数目。
第二行至 n + 1 n+1 n+1 行,每行有两个整数, c i , d i c_i,d_i ci,di,表示第 i i i 朵云的价钱和价值。
第 n + 2 n+2 n+2 至 n + 1 + m n+1+m n+1+m 行 ,每行有两个整数 u i , v i u_i,v_i ui,vi。表示买第 u i u_i ui 朵云就必须买第 v i v_i vi 朵云,同理,如果买第 v i v_i vi 朵就必须买第 u i u_i ui 朵。
输出格式
一行,表示可以获得的最大价值。
样例 #1
样例输入 #1
5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2
样例输出 #1
1
提示
- 对于 30 % 30\% 30% 的数据,满足 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100;
- 对于 50 % 50\% 50% 的数据,满足 1 ≤ n , w ≤ 1 0 3 1 \le n, w \le 10^3 1≤n,w≤103, 1 ≤ m ≤ 100 1 \le m \le 100 1≤m≤100;
- 对于 100 % 100\% 100% 的数据,满足 1 ≤ n , w ≤ 1 0 4 1 \le n, w \le 10^4 1≤n,w≤104, 0 ≤ m ≤ 5 × 1 0 3 0 \le m \le 5 \times 10^3 0≤m≤5×103。
思路
先并查集合并,再用01背包解决即可.
AC代码
#include8.P2814 家谱
P2814 家谱
题目背景
现代的人对于本家族血统越来越感兴趣。
题目描述
给出充足的父子关系,请你编写程序找到某个人的最早的祖先。
输入格式
输入由多行组成,首先是一系列有关父子关系的描述,其中每一组父子关系中父亲只有一行,儿子可能有若干行,用 #name 的形式描写一组父子关系中的父亲的名字,用 +name 的形式描写一组父子关系中的儿子的名字;接下来用 ?name 的形式表示要求该人的最早的祖先;最后用单独的一个 $ 表示文件结束。
输出格式
按照输入文件的要求顺序,求出每一个要找祖先的人的祖先,格式为:本人的名字 + + + 一个空格 + + + 祖先的名字 + + + 回车。
样例 #1
样例输入 #1
#George
+Rodney
#Arthur
+Gareth
+Walter
#Gareth
+Edward
?Edward
?Walter
?Rodney
?Arthur
$
样例输出 #1
Edward Arthur
Walter Arthur
Rodney George
Arthur Arthur
提示
规定每个人的名字都有且只有 6 6 6 个字符,而且首字母大写,且没有任意两个人的名字相同。最多可能有 1 0 3 10^3 103 组父子关系,总人数最多可能达到 5 × 1 0 4 5 \times 10^4 5×104 人,家谱中的记载不超过 30 30 30 代。
思路
难点在于输入输出,其余就是板题
AC代码
#include 9.犯罪集团
题目描述
警察抓贩毒集团。有不同类型的犯罪集团,人员可能重复,集团内的人会相互接触。现在警察在其中一人(0号)身上搜出毒品,认为与这个人直接接触或通过其他人有间接接触的人都是嫌疑犯。问包括0号犯人共有多少嫌疑犯?
输入格式
多样例输入。
每个测试用例以两个整数n和m开头,其中n为人数,m为犯罪集团数。你可以假定0 < n <= 30000和0 <= m <= 500。在所有的情况下,每个人都有自己独特的整数编号0到n−1, 且0号是公认的嫌疑犯。
接下来m行输入,每个犯罪集团一行。每一行从一个整数k开始,它本身表示集团内成员的数量。按照成员的数量,在这个组中有k个整数表示人员。一行中的所有整数都被至少一个空格隔开。
n = 0且m = 0时输入结束。
输出格式
对于每个样例,输出嫌疑犯人数。
样例
样例输入
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0
样例输出
4
1
1
思路
并查集合并后,在查询即可
AC代码
#include10.老旧的桥
题目描述
现在有 n n n个岛屿和 m m m座桥。
第i座桥双向连接着第 A i A_{i} Ai和第 B i B_{i} Bi个岛屿。
刚开始的时候,我们可以用其中的一些桥在任何两个岛之间旅行。
然而,经调查显示,这些桥都将会因老旧而倒塌,而且倒塌的顺序为从第 1 1 1座桥到第 M M M座桥。
由于剩下的桥不能够使第 a a a个岛和第 b b b个岛互相到达,这会使岛屿对 ( a , b ) ( a < b ) (a,b)(a
对于每一个 i ( 1 ≤ i ≤ m ) i(1 \leq i \leq m) i(1≤i≤m),找出在第i座桥倒塌之后,这样不方便的岛屿对 ( a , b ) ( a < b ) (a,b)(a
输入格式
第一行有两个正整数 N N N和 M M M,分别表示岛屿的数量和桥的数量。
接下来有 M M M行,每一行有两个整数 A i A_{i} Ai和 B i B_{i} Bi,分别表示第 i i i座桥连接的两个岛屿的编号。
输出格式
输出有 M M M行,每一行输出一个整数,表示第i座桥倒塌之后不方便到达的岛屿对 ( a , b ) ( a < b ) (a,b)(a
样例
样例输入1
4 5
1 2
3 4
1 3
2 3
1 4
样例输出1
0
0
4
5
6
样例输入2
6 5
2 3
1 2
5 6
3 4
4 5
样例输出2
8
9
12
14
15
样例输入3
2 1
1 2
样例输出3
1
数据范围与提示
所有的输入都是整数。
2 ≤ N ≤ 1 0 5 2 \leq N \leq 10^5 2≤N≤105
1 ≤ M ≤ 1 0 5 1 \leq M \leq 10^5 1≤M≤105
1 ≤ A i ≤ B i ≤ N 1 \leq A_{i} \leq B_{i} \leq N 1≤Ai≤Bi≤N
初始不方便到达的岛屿的数量为 0 0 0
思路
此题类似于
打击犯罪,再运用乘法原理即可
AC代码
#include11.造船
题目描述
小Y想要在虚拟世界里造船。最开始 n n n个船的完成度全部都为 0 0 0。小Y第 i i i时刻可以在 a i a_{i} ai和 b i b_{i} bi两艘船中选择一艘让这艘船的完成度 + 1 +1 +1。
由于国家政府是奇数控,所以所有偶数完成度的船只都将被摧毁,小Y想知道 m m m时刻后能剩下来的船只最多有多少艘。
输入格式
第一行两个整数 n n n和 m m m
接下来 m m m行,每行两个整数 a i , b i a_{i},b_{i} ai,bi
输出格式
输出仅有一个整数,表示 m m m时刻后能剩下来的船只最多有多少艘。
样例
input
8 6
1 2
3 4
4 5
6 7
7 8
8 6
output
6
数据范围与提示
20%的数据, m ≤ 20 , n ≤ 100 m \leq 20,n \leq 100 m≤20,n≤100
20%的数据, n ≤ 20 , m ≤ 100 n \leq 20,m \leq 100 n≤20,m≤100
20%的数据, n ≤ 100 , m ≤ 500 n \leq 100,m \leq 500 n≤100,m≤500
对于40%的数据, 1 ≤ n , m ≤ 200000 1 \leq n,m \leq 200000 1≤n,m≤200000
思路
这道题我们在每次输入时,构建并查集
(这很普通嘛
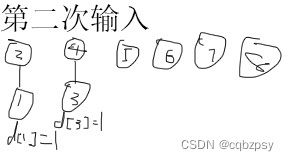
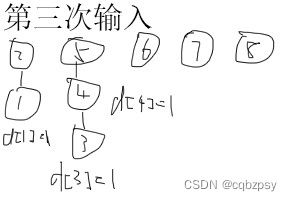
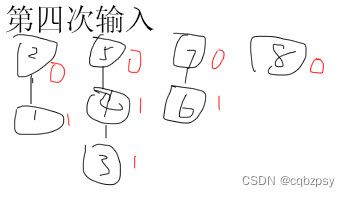
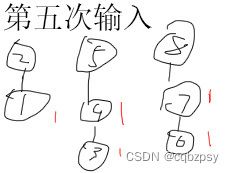
在构建并查集时, 我们只需要让子串保留 1 1 1的完成度然后再让根节点变成偶数的完成度或奇数的完成度
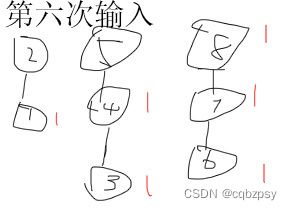
对于样例的解释(如下图):
为了方便以下图片的 d i = x d_i = x di=x,皆用一个红色数字 x x x来表示
最后将 d i d_i di加起来就是答案.
这里我们来深思一下四种情况:1.子串不为 1 1 1 且 r o o t root root 不为 1 1 1 – 将子串置为 1 1 1
2.子串不为 1 1 1 且 r o o t root root 为 1 1 1 – 将子串置为 1 1 1
3.子串为 1 1 1 且 r o o t root root 不为 1 1 1 – 将 r o o t root root 置为 1 1 1
4.子串为 1 1 1 且 r o o t root root 为 1 1 1 – 将 r o o t root root 置为 1 1 1
总结起来就是:
1.子串不为 1 1 1 – 子串置为 1 1 1
2.子串为 1 1 1 – r o o t root root 异或等于 1 1 1
注:异或即
xor与^
作用:将 0 0 0 变成 1 1 1, 将 1 1 1 变成 0 0 0
AC代码
#include12.[NOIP2010 提高组] 关押罪犯
题目描述
S S S 城现有两座监狱,一共关押着 N N N 名罪犯,编号分别为 1 − N 1-N 1−N。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。如果两名怨气值为 c c c 的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为 c c c 的冲突事件。
每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到 S S S 城 Z Z Z 市长那里。公务繁忙的 Z Z Z 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。
在详细考察了 N N N 名罪犯间的矛盾关系后,警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。
那么,应如何分配罪犯,才能使 Z Z Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少?
输入格式
每行中两个数之间用一个空格隔开。第一行为两个正整数 N , M N,M N,M,分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 M M M 行每行为三个正整数 a j , b j , c j a_j,b_j,c_j aj,bj,cj,表示 a j a_j aj 号和 b j b_j bj 号罪犯之间存在仇恨,其怨气值为 c j c_j cj。数据保证 1 < a j ≤ b j ≤ N , 0 < c j ≤ 1 0 9 1
输出格式
共 1 1 1 行,为 Z Z Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件,请输出 0。
样例 #1
样例输入 #1
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
样例输出 #1
3512
提示
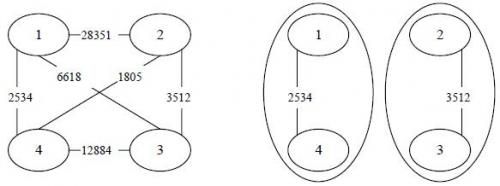
【输入输出样例说明】罪犯之间的怨气值如下面左图所示,右图所示为罪犯的分配方法,市长看到的冲突事件影响力是 3512 3512 3512(由 2 2 2 号和 3 3 3 号罪犯引发)。其他任何分法都不会比这个分法更优。
【数据范围】
对于 30 % 30\% 30%的数据有 N ≤ 15 N\leq 15 N≤15。
对于 70 % 70\% 70% 的数据有 N ≤ 2000 , M ≤ 50000 N\leq 2000,M\leq 50000 N≤2000,M≤50000。
对于 100 % 100\% 100% 的数据有 N ≤ 20000 , M ≤ 100000 N\leq 20000,M\leq 100000 N≤20000,M≤100000。
思路
经典的带权并查集,因此排序是必须的,我们要尽可能让危害大的罪犯在两个监狱里。
那么,再结合敌人的敌人和自己在一个监狱的规律合并。
当查找时发现其中两个罪犯不可避免地碰撞到一起时,只能将其输出并结束。
还有一点很重要,就是没有冲突时一定输出 0 0 0 !!!(如果不输出 0 0 0 只会拿 60 60 60 到 90 90 90 分(分数的差异是因为交的题库不一样))
AC代码
#include13.明辨是非
题目描述
给 n n n组操作,每组操作形式为 x y p。
当 p p p为 1 1 1时,如果第 x x x个变量和第 y y y个变量可以相等,则输出 YES,并限制他们相等;否则输出 NO,并忽略此次操作。
当 p p p为 0 0 0时,如果第 x x x个变量和第 y y y个变量可以不相等,则输出 YES,并限制他们不相等;否则输出 NO,并忽略此次操作。
输入格式
第一行为一个正整数n。 接下来n行每行三个整数 x , y , p x,y,p x,y,p。
输出格式
对于n行操作,分别输出n行 YES 或者 NO。
样例
样例输入
3
1 2 1
1 3 1
2 3 0
样例输出
YES
YES
NO
数据范围与提示
对于前 40 % 40\% 40%的数据, n ≤ 1000 n \leq 1000 n≤1000。
对于前 100 % 100\% 100% 的数据, 1 ≤ n ≤ 1 0 5 , 1 ≤ x , y ≤ 1 0 8 1 \leq n \leq 10^5,1 \leq x,y \leq 10^8 1≤n≤105,1≤x,y≤108 , p ∈ { 0 , 1 } ,p \in \{0,1\} ,p∈{0,1}
思路
看到 x x x 和 y y y 的范围, 我们立刻就想到了离散化
(其实用 m a p map map也不是不行,毕竟我就用的 m a p map map
然后,对于相等的数, 我们用一个并查集来维护,对于每一个不相等的数, 我们都开一个 s e t set set 来维护.
判断方法:
1.当 p p p 为 1 1 1时:
(1)如果 f x fx fx == f y fy fy 输出YES
(2)如果 在 s [ f x ] s[fx] s[fx]中找到了 f y fy fy 输出NO
(3)剩下的情况 输出YES将 s [ f x ] s[fx] s[fx]与 s [ f y ] s[fy] s[fy]合并, 并合并 f a [ f x ] fa[fx] fa[fx]与 f a [ f y ] fa[fy] fa[fy]
2.当 p p p为 0 0 0时:
(1)如果 f x = = f y fx == fy fx==fy 输出NO
(2)剩下的情况输出YES,并将 s [ f x ] s[fx] s[fx]与 s [ f y ] s[fy] s[fy]中分别加入 f y , f x fy,fx fy,fx;
AC代码
#include14.箱子
题目描述
有 n n n个箱子,初始时每个箱子单独为一列;
接下来有p行输入,M x y 或者 C x;
对于M x y:表示将x箱子所在的一列箱子搬到y所在的一列箱子上;
对于C x:表示求箱子x下面(不包含x)有多少个箱子;
输入格式
第一行一个整数 P P P,表示操作次数。
接下来有 p ( 1 ≤ P ≤ 100000 ) p(1 \leq P \leq 100000) p(1≤P≤100000)行输入,M x y 或者 C x;(x,y<=N)
箱子的个数 N N N,不会出现在输入中。 ( 1 ≤ N ≤ 30000 ) (1 \leq N \leq 30000) (1≤N≤30000),初始时每个箱子单独为一列;你可以认为,操作过程中,不会出现编号大于 30000 30000 30000的箱子
输出格式
对于每个询问,输出相应的值。
样例
样例输入
6
M 1 6
C 1
M 2 4
M 2 6
C 3
C 4
样例输出
1
0
2
思路
跟
银河英雄传说几乎一样
AC代码
#include15.[NOI2015] 程序自动分析
题目描述
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 x 1 , x 2 , x 3 , ⋯ x_1,x_2,x_3,\cdots x1,x2,x3,⋯ 代表程序中出现的变量,给定 n n n 个形如 x i = x j x_i=x_j xi=xj 或 x i ≠ x j x_i\neq x_j xi=xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为: x 1 = x 2 , x 2 = x 3 , x 3 = x 4 , x 4 ≠ x 1 x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1 x1=x2,x2=x3,x3=x4,x4=x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入的第一行包含一个正整数 t t t,表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第一行包含一个正整数 n n n,表示该问题中需要被满足的约束条件个数。接下来 n n n 行,每行包括三个整数 i , j , e i,j,e i,j,e,描述一个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e = 1 e=1 e=1,则该约束条件为 x i = x j x_i=x_j xi=xj。若 e = 0 e=0 e=0,则该约束条件为 x i ≠ x j x_i\neq x_j xi=xj。
输出格式
输出包括 t t t 行。
输出文件的第 k k k 行输出一个字符串 YES 或者 NO(字母全部大写),YES 表示输入中的第 k k k 个问题判定为可以被满足,NO 表示不可被满足。
样例 #1
样例输入 #1
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
样例输出 #1
NO
YES
样例 #2
样例输入 #2
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0
样例输出 #2
YES
NO
提示
【样例解释1】
在第一个问题中,约束条件为: x 1 = x 2 , x 1 ≠ x 2 x_1=x_2,x_1\neq x_2 x1=x2,x1=x2。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为: x 1 = x 2 , x 1 = x 2 x_1=x_2,x_1 = x_2 x1=x2,x1=x2。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个: x 1 = x 2 , x 2 = x 3 , x 3 = x 1 x_1=x_2,x_2= x_3,x_3=x_1 x1=x2,x2=x3,x3=x1。只需赋值使得 x 1 = x 2 = x 3 x_1=x_2=x_3 x1=x2=x3,即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个: x 1 = x 2 , x 2 = x 3 , x 3 = x 4 , x 4 ≠ x 1 x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1 x1=x2,x2=x3,x3=x4,x4=x1。由前三个约束条件可以推出 x 1 = x 2 = x 3 = x 4 x_1=x_2=x_3=x_4 x1=x2=x3=x4,然而最后一个约束条件却要求 x 1 ≠ x 4 x_1\neq x_4 x1=x4,因此不可被满足。
【数据范围】
注:实际上 n ≤ 1 0 6 n\le 10^6 n≤106 。
思路
并查集的裸题,只需要一个离散化就好了.
AC代码
#include