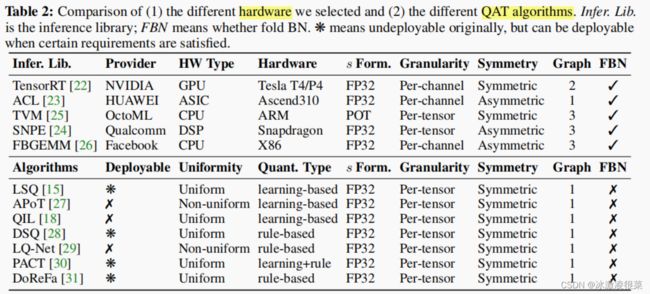
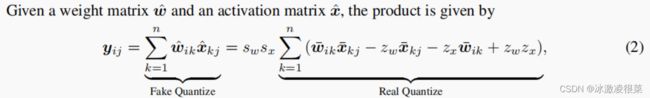MQBench: Towards Reproducible and Deployable Model Quantization Benchmark 论文学习
论文链接
摘要
模型量化已成为加速深度学习推理不可或缺的技术。当研究人员继续推动量化算法的前沿时,现有的量化工作往往是不可重复和不可部署的。这是因为研究人员没有选择一致的训练流程,并且了硬件部署的需求。在这项工作中,我们提出了模型量化基准测试(MQBench),这是第一次评估、分析和基准测试模型量化算法的再现性和可部署性的尝试。我们为现实世界的部署选择了多个不同的平台,包括CPU、GPU、ASIC、DSP,并在一个统一的训练框架流程下评估广泛的最先进的量化算法。MQBench就像一个连接算法和硬件的桥梁。我们进行了全面的分析,并发现了相当多的直觉或反直觉的见解。通过调整训练设置,我们发现现有算法在传统学术轨道上具有相同的性能。而对于硬件可部署的量化,仍存在一个巨大的精度差距仍然有待解决。令人惊讶的是,没有一种现有的算法能赢得MQBench的每一个挑战,我们希望这项工作能够启发未来的研究方向。
1. 引言
我们指出了量化研究中两个长期被忽视的关键因素,即可再现性和可部署性。首先,我们观察到训练超参数可以显著影响量化网络的性能。以Esser等人,[15]采用余弦退火学习学习速率[16]和更好的权重衰减选择,将2位ResNet-18[17]在ImageNet上的前1位精度分别提高了0.7%和0.4%。全精度网络预训练也可以提高量化结果[15,18]。再现性问题在其他领域也得到了相当多的关注,例如NAS-Bench-101[19]。到目前为止,还缺乏一个统一训练流程,并在全面和公正的意义上比较量化算法的基准。
其次,我们发现大多数的学术研究论文并没有在真正的硬件设备上测试他们的算法。因此,所报告的性能可能并不可靠。首先,硬件会将将批处理规范化(BN)层[20]折叠为卷积层[3],以避免额外的开销。但大多数研究论文只是保持了BN层的完整。另一方面,研究论文只考虑了对卷积层的输入参数和权值参数的量化。而在部署过程中,整个计算图都应该被量化。这些规则将不可避免地使量化算法的弹性降低。另一个较少研究的问题是算法的鲁棒性:如果一个算法应用于每通道量化,但它首先被设计为每张量量化,会发生什么?该算法应考虑到量化器设计的多样性。所有这些问题表明学术研究和现实世界部署之间存在很大的差距。
在这项工作中,我们提出了模型量化基准(MQBench),这是一个设计用于在多个现实硬件环境中分析和再现量化算法的框架(见图1和表1)。我们仔细研究了现有的量化算法和硬件部署设置,从而建立了算法和硬件之间的桥梁。为了完成MQBench,我们利用了超过50GPU年的计算时间,以努力促进量化研究中的再现性和可部署性。同时,我们的基准提供了一些被忽视的观察结果,这可能指导进一步的研究。据我们所知,这是第一个在多个通用硬件平台上基准测试量化算法的工作。
2.MQBench:走向可重复性的量化
在本节中,我们对量化算法的可再现性进行了基准测试,主要包括量化感知训练(QAT)2。我们评估了算法在ImageNet[21]分类任务上的性能。其他任务,如检测,分割和语言应用目前没有考虑,因为很少有基线算法被提出。MQBench评估在4个维度中执行:支持的推理库,给定了特定的硬件、量化算法、网络架构和位宽。
硬件感知量化器
3. MQBench:实现可部署的量化
3.1假的和真实的量化
3.2 BN 融合
![]()
以下是本人个人的解读:大家参考着看,有错误的,欢迎交流哈~
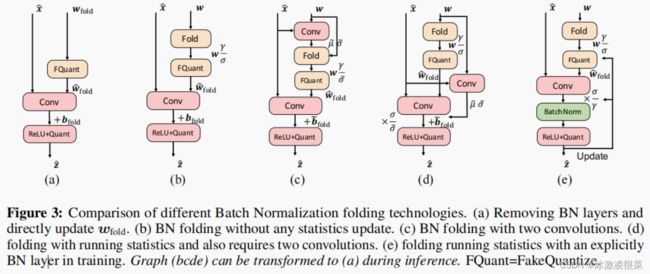
(a)将BN的参数融合到conv中,且不更新γ,β,μ,σ2。
过程:融合后的权重经过量化——反量化与量化后的输入卷积,加上全精度的偏置之后经过relu并量化后得到量化后的输出后。
备注:此方案其实是推理的过程,在训练过程中由于没有BN 容易导致梯度爆炸。
(b)将BN融合,但是正在运行的μ~,σ2 ~ 不会被更新,但是γ以及β会被SGD更新。
过程:融合后的权重中的γ被更新经过量化反量化之后得到新的权重,其与量化后的输入卷积,此时被β,伽马更新的偏置被更新,卷积后的值执行偏移后通过relu量化后得到输出。
备注:我们发现,即使没有更新任何统计数据μ~,σ2 ~ ,该策略仍然可以平滑损失,并达到相当的准确性。这种折叠策略也通过避免统计同步而显著减少了训练时间。
(c)第一次量化后的输入以及FP32权重卷积后更新正在运行的μ~,σ2 ~ 。融合后的权重中的γ,σ2 ~被更新,量化——反量化得到新的权重与量化后的输入卷积,再与经过更新(γ,σ2 ~ ,β)的且融合后偏置运行移位,最后经过relu,量化,得到输出。
备注:在推理过程中,权重和偏差将使用运行均值和方差进行折叠,如在等式中 (4).
(d)(右侧第一个卷积)浮点权重经过第一层卷积后更新了现在运行的μ~,σ2 ~,其更新了融合后的偏置。(中间)同时浮点权重经过融合后经过量化——反量化得到融合后的权重(此时权重是未被当前μ,σ更新的,为了减少本次数据对权重的影响很大。我的理解与原论文正好相反。大家可以看看原文理解下)。此刻量化后的输入以及得到的权重第二次卷积,并通过更新融合后的偏置,在第二次卷积后,将使用批处理方差因子来重新缩放输出,如图3(d).所示。最后还是通过relu 以及量化得到输出。
(e)全精度的权重融合后经过量化——反量化得到新的权重,再与量化后的输入卷积,乘以缩放因子σ/γ,之后经过BN,最后relu以及量化得到输出,输出此时会反向传播更新缩放因子。
备注:在PyTorch量化repo[38]中引入的,这个选项不需要花费两次卷积,而是在量化卷积之后显式地添加了BN层。这种策略带来的好处之一是,批统计数据是基于量化的权重来计算的。在推理过程中,输出σ/γ的重新缩放可以被BN中和,因此图可以转换为图3(a).
3.3方块图
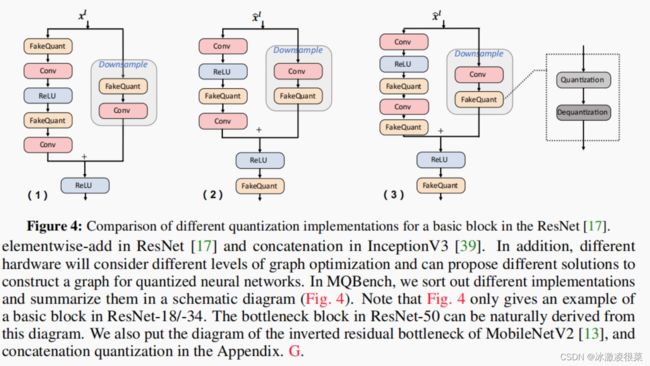
左图显示了量化一个基本块的传统学术实现。只有卷积层的输入将被量化为8位。(请注意,在学术论文中,INT8同时意味着量化和去量化。)块输入和输出以及元素-添加所有在全精度操作。因此,网络吞吐量并没有降低,并且将显著影响延迟。在某些架构中,这个图甚至不会带来任何加速,因为延迟主要由I/O主导。另一个问题是下采样块中激活的单独量化,这也带来了不期望的成本。
中间是NVIDIA的基本块的TensorRT[22]实现。我们可以发现,输入和输出必须量化到低位,以减少数据吞吐量。低位输入可以确保两个分支将在下采样块中使用相同的量化激活。对于元素逐加层,由于与前卷积层的偏置加之一的融合,将以32位模式进行。因此,只有它的一个输入将被量化。
图4右侧展示了其他硬件库的实现,如FBGEMM[26]和TVM[25]。唯一的区别是,它们需要元素添加的所有输入都被量化。在4位对称量化中,这将严重影响精度。
5.MQBench评估
在本节中,我们将对量化算法、网络架构和硬件进行全面的评估和分析。我们研究了由➀测试精度给出的几个评价指标:ImageNet验证集上的前1精度,直接反映了算法的任务性能;➁硬件差距:硬件与学术测试精度的差异,该指标可以反映可部署量化对算法的影响;➂硬件鲁棒性:5个硬件环境下的平均测试精度。➃架构的鲁棒性:在5种网络架构上的平均测试精度。
5.1根据学术设置进行评估
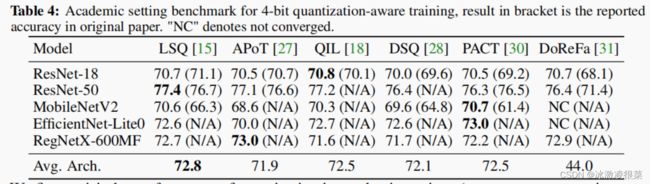
➀算法之间的差异并不像原论文中报道的那么显著。
➁没有一种算法在每个架构上都能达到最佳或最差的性能。
➂基于规则的算法可以实现与基于学习的算法相当的性能。
5.2使用图实现进行评估
图1、2、3对应于图4(a)、(b)、©.中的图实现通过BN折叠实验,我们修改了学术设置,而只改变了图的实现。本研究选择了PACT和LSQ,在ResNet-18和MobileNetV2上进行。表5中的结果显示了最终的性能。我们发现:与对算法很敏感的BN折叠不同,图的实现对网络体系结构很敏感。例如,PACT对ResNet-18的准确率只下降了1.1%。然而,在MobileNetV2上的差距可能会增加到2.9%。在LSQ中也观察到同样的趋势,在ResNet-18和MobileNetV2上分别观察到0.4%和3.6%的精度下降。
5.3使用BN折叠法进行评估
然后,我们研究了为QAT设计的BN折叠策略。我们选择LSQ[15]和PACT[30],运行在ResNet-18和MobileNetV2上进行消融研究。在这里,我们不使用任何真正的硬件感知量化器,而只是修改了传统的学术设置(即每张量,对称的),以适应BN折叠。结果汇总见表6。在我们的实验中,我们有以下观察结果:
➀BN折叠对量化算法很敏感,策略e一般效果最好。
➁策略e没有获得任何比策略c,d显著的加速,即使它只计算一次性卷积。虽然策略e在前向计算中比c,d快,因为它的计算速度较少,但在梯度计算中速度要慢得多。在ResNet-18LSQ上,我们发现策略e进行反向传播的时间比2,3多80%。
➂像LSQ这样的bn折叠友好算法可能不需要更新批统计。例如,在LSQ中使用策略b只比那些更新批均值和方差的人下降0.2%∼0.3%。此外,策略1可以比它们快30%的∼,50%,因为它不需要计算或同步统计数据,而且有更快的反向传播。
➃数据并行分布式学习中BN统计量的同步可以提高准确性。在使用正常BN的分布式训练中,跨设备的异步BN统计数据是可以接受的,只要批处理大小相对较大,就不会影响最终的性能。然而,在QAT中,将BN折叠成具有异步统计量的权值会产生不同的量化权值,进一步放大了训练的不稳定性。同步需要时间,因此它是一个精度-速度的权衡。SyncBN可以提高PACTResNet-182.3%的准确率。
➄折叠BN在初始训练阶段会导致严重的不稳定,这可以通过学习率热身来有效地缓解。如果没有热身,大多数具有BN折叠的QAT将无法收敛。因此,对于所有需要BN折叠的其余实验,我们采用1epoch学习率线性热身、同步BN统计和策略e来促进它。

5.4 4位QAT
在本节中,我们通过使用可部署的和可重复的基准测试来比较一些流行的算法,为现有的和未来的工作建立了一个主要的基线。我们实验使用了4位量化感知训练。与表4中4位量化几乎无损的学术设置不同,我们展示了可部署量化的挑战性。和[19]一样,我们的目的并不是要对“哪种方法在这个基准测试上效果最好?””,而是为了演示一个可重复和可部署的基线的实用性。并希望,有了新发现的见解,我们可以指导未来对量化算法的研究。主要结果见表7。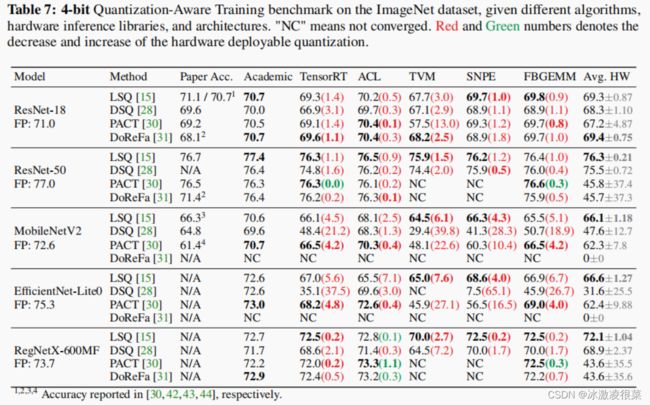
测试精度
我们将该算法应用于5个不同的真实硬件部署环境并报告了他们的假量化性能。我们首先访问绝对测试的准确度。从表中可以看出,我们观察到没有一种算法在每个设置上都能达到最佳的绝对性能。在25个设置(5个架构×5硬件环境)中,LSQ[15]在52%的情况下获得了最好的性能。PACT[30]和DoReFa[31]获得了其余38%和10%的最佳实践。虽然DSQ[28]没有实现任何最佳实践,但我们永远不应该把它排到最后一个。在许多情况下,DoReFa和PACT确实不能收敛,而DSQ可以具有良好的性能。我们不能简单地基于单个度量对每个算法进行排序。我们还研究了测试精度的分布。在图5中,我们展示了不同硬件和网络体系结构组合下的测试精度的标准偏差。这个度量测量了算法之间的性能差异。方差越小,意味着算法之间的区别越小。根据图5,我们发现网络(MobileNetV2和 EfficientNet-Lite)和per-tensor量化(TVM和SNPE)有很大的方差。因此,我们建议在今后的研究中更加关注它们。
硬件差距
我们还研究了硬件差距度量,这意味着在从学术设置过渡到硬件设置时的退化。这些值在表中用彩色数字标记。值得注意的是,93%的实验遇到了精度下降。其中,25.8%的设置准确率下降在1.0%以内,47.3%的设置准确率下降在3.0%以内。与我们在绝对精度方面的发现相似,没有一种算法在每个设置中都能达到最小的硬件差距。LSQ只有36%的概率赢得硬件差距度量,而PACT的概率为48%。
硬件和架构的鲁棒性
我们在图6中验证了其架构和硬件的鲁棒性。为了实现体系结构的鲁棒性,我们发现了三种类型的模式。在ResNet-18上,每个算法都可以收敛到较高的精度,而ResNet-50和RegNet与ResNet-18共享不同的模式。最后,MobileNetV2和高效Net-Lite也有类似的算法性能。这表明,网络体系结构对量化算法可能有不同的敏感性。
我们还探讨了量化算法在应用于各种硬件时的鲁棒性。一般来说,LSQ具有最好的硬件鲁棒性。它在不同的硬件上带来了更稳定的性能。然而,我们发现LSQ并不适合用于每通道的量化。对于所有15个每通道的硬件设置,LSQ只赢得了23%的案例,而66.7%的奖杯是由PACT声称获得的。LSQ在每张量量子化方面表现出令人兴奋的优势,它赢得了90%的情况。这一结果表明了硬件鲁棒性度量的重要性。
对算法选择的建议
虽然在QAT中没有针对所有情况的单一算法是SOTA,但算法的选择有一些潜在的规则。根据图6,我们发现LSQ在每张量量化(SNPE和TVM)中通常表现最好,而PACT在每通道量化(TensorRT,ACL,FBGEMM)中表现最好。因此,我们建议使用PACT进行每通道量化,使用LSQ进行每通道张量量化。如果之前没有达到目标硬件或网络架构,我们建议使用LSQ,因为它具有历史上最好的平均性能(图6)。请注意,并不是所有的情况都需要仔细地选择算法。由图5可以看出,在每通道量化和非深度卷积网络的情况下,算法的方差很低。因此,在这些设置下,算法的选择是很简单的。
6. 总结
在这项工作中,我们介绍了MQBench,一个关于量化算法和硬件的系统表格研究。为了提高再现性,我们对齐了训练超参数和量化算法的管道。为了提高可部署性,我们整理了5个硬件部署设置,并在5个网络架构中对这些算法进行了基准测试。我们进行了全面的评估,重点关注模型量化中较少探索的方面,包括BN折叠、图实现、硬件感知量化器等。然而,MQBench也有局限性,量化在目标检测和NLP应用等部署中面临着更多的挑战。更先进的算法(如无数据量化[45,46,47])也需要进行一个完整的基准测试。这些方面应在今后的工作中加以研究。尽管如此,我们希望MQBench将是量化领域不断改进的严格基准序列中的第一个。