Python：异常值检测箱型图（附：正态分布3σ）

        异常值检测的方法有很多，通过数据分布图型寻找异常值、算法模型（聚类、随机森林等），我这里就是记录一下工作中做初步的数据探查时用到的箱型图检测和正态分布检测，这两种都是根据数据分布情况来识别异常值的，没有结合到业务的层面，在做初步的探查时还是高效且适用的。因为正态分布3σ的异常值检测需要数据符合正态分布，现实情况中大部分数据都是杂乱无章的，因此重点使用的是箱型图检测。

1.箱型图的优势

（1）准确稳定地描绘出数据的离散分布情况且不需要服从特定的分布形式

箱形图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；

（2）异常值不会影响四分位数的确定

箱形图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱形图识别异常值的结果比较客观。

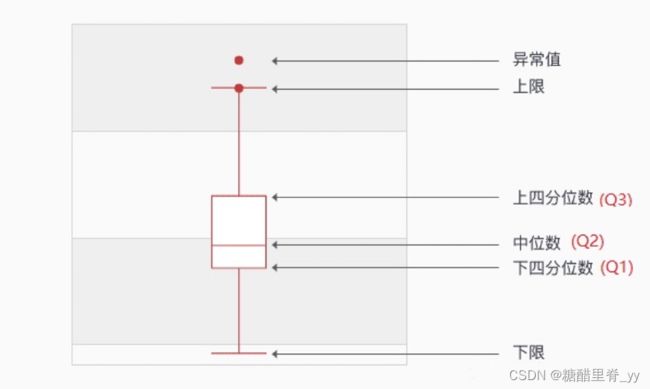
2.箱型图的示意及符号说明

（图片来源于网络）

Qi所在位置=i（n+1）/4，其中i=1，2，3。n表示序列中包含的项数。根据所在位置找到此位置上的数据。

下四分位数Q1：该样本中所有数值由小到大排列后第25%的数字。

中位数Q2：该样本中所有数值由小到大排列后第50%的数字

上四分位数Q3：该样本中所有数值由小到大排列后第75%的数字

四分位距IQR：IQR=Q3-Q1

上限：非异常范围内的最大值，上限=Q3+1.5IQR

下限：非异常范围内的最小值，下限=Q1-1.5IQR

3.Python代码

def OutlierDetection_box(df,con,path):#con代表数据列的名称，path代表文本保存的路径
    # 计算下四分位数和上四分位
    Q1 = df.quantile(q=0.25)
    Q3 = df.quantile(q=0.75)
    Q2 = df.quantile(q=0.5)

    # 基于1.5倍的四分位差计算上下须对应的值
    low_whisker = Q1 - 1.5 * (Q3 - Q1)
    up_whisker = Q3 + 1.5 * (Q3 - Q1)

    # 寻找异常点
    outliers = df[(df > up_whisker) | (df < low_whisker)]
    #data1 = pd.DataFrame({'id': kk.index, '异常值': kk})
    
    #统计，stat_ll为箱型图中数据分布情况（多个数据列合并最后会输出一个sheet页），f最后会输出一个标识具体数据点的文本
    dataQ3=df[(df>Q2) & (df<=Q3)]
    countQ3=len(dataQ3)
    dataQ1 = df[(df < Q2) & (df >= Q1)]
    countQ1 = len(dataQ1)
    data_max = df[(df <= up_whisker) & (df > Q3)]
    count_max = len(data_max)
    data_min = df[(df >= low_whisker) & (df < Q1)]
    count_min = len(data_min)
    stat_ll=[con,countQ3,countQ1,count_max,count_min]
    with open(path+"/box_new.txt", "a",encoding='utf-8') as f:
        f.write("\n%s的箱型图分布统计如下："%con)
        f.write("\n箱线图检测到的异常值如下：")
        f.write(str(outliers.to_dict()))
        f.write("\n落入中位数到上四分位距有%d条，具体如下："%countQ3)
        f.write(str(dataQ3.to_dict()))
        f.write("\n落入中位数到下四分位距有%d条，具体如下：" % countQ1)
        f.write(str(dataQ1.to_dict()))
        f.write("\n落入上四分位数到最大值有%d条，具体如下：" % count_max)
        f.write(str(data_max.to_dict()))
        f.write("\n落入下四分位数到最小值有%d条，具体如下：" % count_min)
        f.write(str(data_min.to_dict()))
    return outliers,stat_ll

 2.正态分布

def OutlierDetection_std(df,con,path):
    # 计算均值
    u = df.mean()
    # 计算标准差
    std = df.std()
    # 计算P值
    res = kstest(df, 'norm', (u, std))[1]
    if res <= 0.05:#判断是不是符合正态分布
        # 定义3σ法则识别异常值
        # 识别异常值
        error_low = df[np.abs(df - u) > 2 * std]
        error_high = df[np.abs(df - u) > 3 * std]
        # 剔除异常值，保留正常的数据
        #data_normal = df[np.abs(df - u) <= 3 * std]
        with open(path+"/std_outliers.txt", "a", encoding='utf-8') as f:
            f.write("\n%s符合正态分布："%con)
            f.write("\n2sigma异常值如下：")
            f.write(str(error_low.to_dict()))
            f.write("\n3sigma异常值如下：")
            f.write(str(error_high.to_dict()))
        return u, std, error_low, error_high

    else:
        logger.info('该数据不服从正态分布-----------')
        return None

3.正态分布结合四分位距（网上一篇文章看到的，实际没有使用）

def box_3Sigma(df,sigma):
    Q1 = df.quantile(q=0.25)
    Q3 = df.quantile(q=0.75)
    IQR = Q3 - Q1
    min = Q1 - 1.5 * IQR
    max = Q3 + 1.5 * IQR
    ratio = 0.3
    low = 3*sigma * ratio + min * (1 - ratio)
    hight = 3*sigma * ratio + max * (1 - ratio)