用s函数实现Lugre摩擦模型

目录

1. Lugre摩擦模型

2. Lugre摩擦模型的状态空间方程

3. Lugre摩擦模型的simulink建模

4. Lugre摩擦模型的s函数建模

5. simulink模型和s函数模型对比

6. Lugre摩擦模型的s函数源代码

---

1. Lugre摩擦模型

        摩擦模型主要分为动态和静态摩擦模型。Lugre摩擦模型能够很好的反应出摩擦的静态和动态效应。Lugre摩擦模型：

                        ①

                ②

        其中为非线性函数：

   ③

表1 参数意义及取值

参数	意义	本文取值
	接触面相对角速度	——
z	鬃毛的平均形变	——
	库伦摩擦力	2.4440
	最大静摩擦力	0.5991
	Stribeck速度	0.0103
	鬃毛刚性系数	0.4766
	滑动阻尼系数	0.2701
	黏性摩擦因数	0.0049

         这些参数根据不同的系统取不同的值，且会在外界温度、润滑条件、材料磨损及接触面作用力等因素的影响下发生改变（取值方法：查论文，一般通过参数辨识来计算取值；以上取值仅为示例）

2. Lugre摩擦模型的状态空间方程

          ④

                   ⑤

        其中，T为离散采样时间，

        

        取状态变量：

                          ⑥

        则根据表达式④、⑤有状态方程：

         ⑦

        根据表达式②有输出方程：

                      ⑧

3. Lugre摩擦模型的simulink建模

        根据表达式 ①②③搭建simulink仿真模型如图1所示：

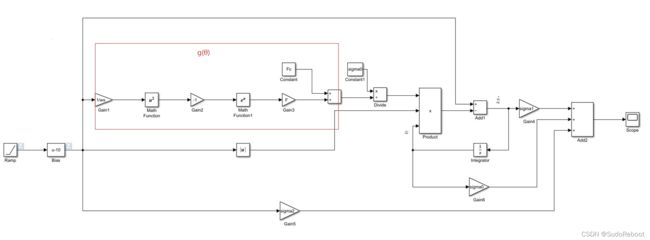图1 Lugre的simulink仿真

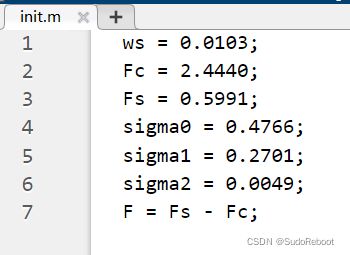
        参数初始化：（按照表1中参数初始化，仿真前先运行init.m文件，将参数加载到工作空间）

图2 参数初始化

        输入信号：                                                

图3 输入信号

        输出波形：

图4 输出波形

4. Lugre摩擦模型的s函数建模

        根据表达式⑦⑧和表1中的参数编写s函数，取离散采样时间为0.001s：

   ⑨

                                       ⑩

        离散变量、输入、输出设置：

sizes.NumDiscStates  = 2;   %离散变量个数
sizes.NumOutputs     = 1;   %输出个数
sizes.NumInputs      = 1;   %输入个数

        初始条件设置：

x0  = [0;0];

        采样时间设置：

ts  = [0.001 0];

        表达式⑨：

function sys=mdlUpdate(t,x,u)
w = u(1);
gw = 2.4440 + (0.5991 - 2.4440)*exp(-(w/0.0103)^2);
sys = [1 0.001;-0.4766*((abs(w))/gw) 0]*x+[0;1]*w;

        表达式⑩：

function sys=mdlOutputs(t,x,u)
w = u(1);
sys = [0.4766 0.2701]*x+0.0049*w;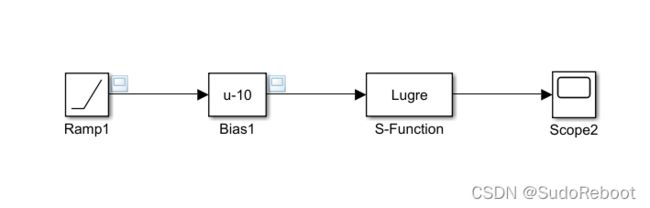

图5 s函数的Lugre仿真

 输入波形：

图6 输入信号

 输出波形：

图7 输出波形

5. simulink模型和s函数模型对比

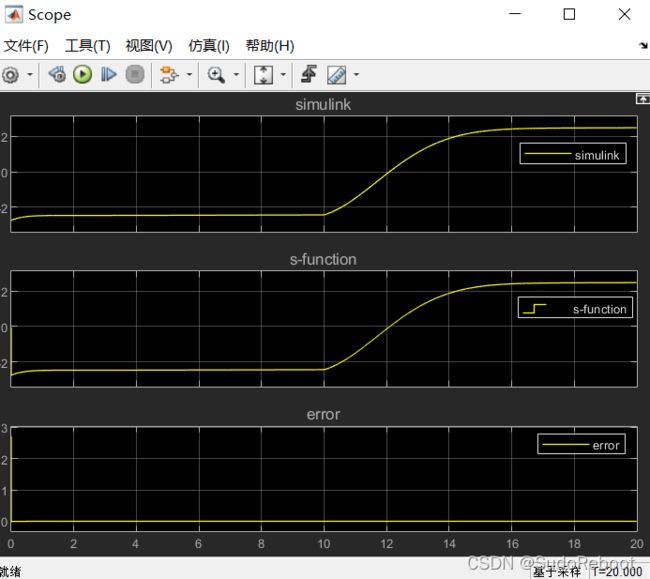
图8 simulink模型和s-function模型对比

         图8中上半部分为simulink模型，下半部分s-function模型

图9 仿真结果对比

         根据图9可知s函数模型和simulink模型输出波形基本一致。s函数离散变量的初始状态会影响0时刻的仿真值，修改s函数离散变量初始值会减小0时刻的误差。

x0  = [0;-10];

图10 修改初始状态后的仿真结果

         误差在0.001级，可以忽略。

6. Lugre摩擦模型的s函数源代码

function [sys,x0,str,ts,simStateCompliance] = Lugre(t,x,u,flag)

switch flag
  case 0   %初始化
    [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;

  case 1   %计算连续状态的微分
    sys=mdlDerivatives(t,x,u);

  case 2   %计算下一个离散状态  
    sys=mdlUpdate(t,x,u);

  case 3   %计算输出
    sys=mdlOutputs(t,x,u);

  case 4   %计算下一次采样的时间
    sys=mdlGetTimeOfNextVarHit(t,x,u);

  case 9   %系统结束
    sys=mdlTerminate(t,x,u);

  otherwise %其他情况
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));

end

%case 0:初始化
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes

sizes = simsizes;           %用于设置模块参数的结构体

sizes.NumContStates  = 0;   %连续变量个数
sizes.NumDiscStates  = 2;   %离散变量个数
sizes.NumOutputs     = 1;   %输出个数
sizes.NumInputs      = 1;   %输入个数
sizes.DirFeedthrough = 1;   %输入是否直接影响输出
sizes.NumSampleTimes = 1;   %至少一个采样时间

sys = simsizes(sizes);

%初始化初始条件
x0  = [0;0];

%保留项
str = [];

% 初始化采样时间
ts  = [0.001 0]; %[0 0] 连续采样
             %[0 1] 小步长的连续采样
			 %[PERIOD OFFSET] 离散采用时间 [采样时间 步长]
			 %[-2 0] 变步长的采样时间 FLAG=4时获取下一次采样时间

%指定simStateCompliance块值
simStateCompliance = 'UnknownSimState'; %'UnknownSimState'  默认设置
										%'DefaultSimState'  与内置块的模拟状态相同
										%'HasNoSimState'    没有模拟状态
										%'DisallowSimState' 保存或恢复模型模拟状态时出错


%case 1:计算连续状态的微分
%sys=AX+BU
function sys=mdlDerivatives(t,x,u)
sys = [];

%case 2:计算下一个离散状态  
%sys=AX+BU
function sys=mdlUpdate(t,x,u)
w = u(1);
gw = 2.4440 + (0.5991 - 2.4440)*exp(-(w/0.0103)^2);
sys = [1 0.001;-0.4766*((abs(w))/gw) 0]*x+[0;1]*w;

%case 3:计算输出           
%sys = CX+DU
function sys=mdlOutputs(t,x,u)
w = u(1);
sys = [0.4766 0.2701]*x+0.0049*w;

%case 4:计算下一次采样的时间[-2 0]时使用该函数
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 0.01;    
sys = t + sampleTime;

%case 9:系统结束
function sys=mdlTerminate(t,x,u)
sys = [];