数学建模作业与学习笔记

拟合插值

一维插值：interp(x,y,X,method,‘exrap’)

求出函数表达式y=f(x)，并返回在X曲间的插值Y
细节：
x,y: 构造函数表达式的初始数据
X：插值区间
method =‘nearest’:最邻近点插值(最简单)
‘linear’: 线性插值
‘spline’: 三次样条插值(非线性)

‘exrap’：对于超出x范围的X中的分量执行特殊的外插值方法exrap
应用：题目2

二元插值：griddata(x,y,z,cx,cy,‘method’)

步骤：
①用二元函数z=f(x,y)拟合不规则的数据向量x,y,z。
②返回曲面z在点(cx,cy)处的插值cz
通常：cx,cy是规则的格点（用命令meshgrid生成）
细节：
method =‘linear’ 基于三角型的线性插值
‘cubic’ 基于三角形的三次插值
‘nearest’ 最邻近插值法
‘v4’ matlab4中的griddata算法
应用：题目1

二元二次拟合：regress(y,X)

调用格式：
b =regress(y,X);
[b,bint] =regress(y,X);
[b,bint,r] =regress(y,X);
[b,bint,r,rint] =regress(y,X);
[b,bint,r,rint,stats] =regress(y,X);
参数解释：
y:因变量 X:自变量的可能二元二次线性组合
B：回归系数
bint: 回归系数区间估计(95%置信度)
r: 残差
rint: 残差置信区间(95%)
stats: 检验回归模型的统计量。有四个数值：1.判定系数R^2，F统计量观察值，检验P值，误差方差的估计（第三个参数P值越小<0.001说明模型有效）
代码与注意细节：

%初始数据向量化
X =[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5]';
Y =[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5]'; 
Z =[4 8 6 8 6 8 8 9 9 8 8 9 4 9]';  
%特别注意：向量为n*1格式，1*n格式均需要转置
M =[X.^2,Y.^2,X.*Y,X,Y,ones(size(X))];
[b,bint,r,rint,stats] =regress(Z,M);
%Z =0.0004*X^2+0.0002*Y^2-0.0001*X*Y-0.1108*X-0.0130*Y+14.2395

题目1：海水深度问题

首先想到，可以使用一般的二维插值方法interp2(X,Y,Z,x,y,‘method’)求解，但是该方法要求X,Y为递增向量。本题中给定的平面坐标为离散点，不能使用该方法求值。此时便可以尝试girddata处理不规则的数据向量。

%x y z初始数据（平面坐标与对应深度）向量化
x =[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y =[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z =[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
%（1）网格化cx cy
[cx,cy] =meshgrid(75:5:200,-70:5:150);
%（2）拟合z=f(x,y)并返回插值cz=f(cx,cy)
cz =griddata(x,y,z,cx,cy,'v4');
%（3）网格化图形可视化
surf(cx,cy,cz)
figure(2)
%（4）绘制等高线 countour() and clabel()
[c,h] =contour(cx,cy,cz);
clabel(c,h)  %增加等高线标识

最终可以得到海底图像与等高线图如图：

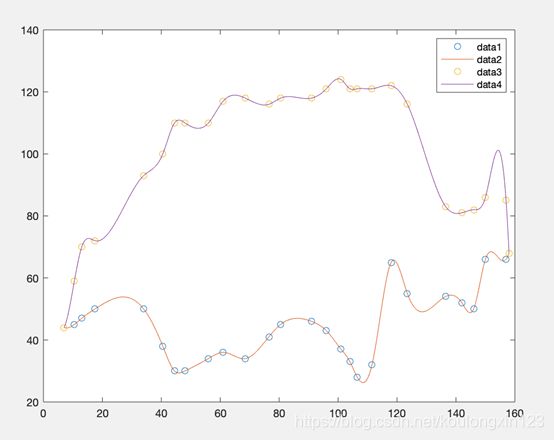
题目2：国土面积计算

假设y1=f(x),y2=g(x)是南北边界分界线纬度与精度（平面坐标）的关系。问题一：分析数据可知,x为规则的数据向量，可以采用interp1(x,y,X,‘method’)方法进行一维数据插值得到曲间[7,158]按间隔0.1mm的横纵坐标数据。并可视化南北分界线确定国土区域。问题二：利用数值积分法求解上下边界曲线所围面积。将面积分成若干小长方形(本题中是0.1mm间隔)并分别求出这些长方形相加面积后通过比例关系转化为面积的近似解

%(1) 曲间[7.158]以0.1mm间隔的数据
X =7:0.1:158;
%(2) 采用三次样条插值(国土区域非线性)得到X数据
ys =interp1(x,y1,X,'spline');
yn =interp1(x,y2,X,'spline');
%(3) 插值与初始数据可视化
plot(x,y1,'o',X,ys)
hold on
plot(x,y2,'o',X,yn)
&（4）数值积分法求解曲线所围面积
s =sum(yn,ys)*0.1/1600*18

结果如图：

s =4.24468e+0.4

微分方程模型

基础模型

题目3 慢跑者与狗

回归模型

4.1多元线性回归

[b,bint,r,rint,stats]=regress(y,x)
b:回归系数
bint:回归系数置信区间
r:残差
rint:残差的置信区间
stats:R^2 ,F,p,s^2

例1：一元线性回归与异常点剔除

步骤：
①画出散点图，判断大致的线性/非线性关系
②regress和rcoplot回归与异常点剔除

clc,clear
x =0.1:0.01:0.18;
y =[42.0 41.5 45.0 45.5 45.0 47.5 49.0 55.0 50.0];
%（1）先画出散点图，判断大致线性关系
figure(1)
plot(x,y,'+');
%（2）regress和rcoplt:数据格式化+系数、图像分析
x1 =x';
y =y';
x=[ones(size(x1)),x1];
%格式：样本数n为列，第一列加上1
[b,bint,r,rint,stats] =regress(y,x);
b
bint
stats
figure(2)
rcoplot(r,rint);

1.图像分析

2.系数分析
b =27.4722 137.5000
bint =18.6851 36.2594（βˆ 的置信区间是[18.6851,36.2594]） 75.7755 199.2245 （βˆ 的置信区
间是[75.7755,199.2245]）
stats =0.7985（R^2复判定系数） 27.7469（F回归模型假设检验） 0.0012（概率p） 4.0883（残差的方差s^2）

3.结论
回归模型：y =27.4722+137.5*x1
其中（1）R^2复判定系数<0.8，相关关系不成立（2）rcoplot图发现异常点（第八数据点）因此删除第八数据点后修改回归结果

clc,clear
x =0.1:0.01:0.18;
y =[42.0 41.5 45.0 45.5 45.0 47.5 49.0 55.0 50.0];
%**********
x(:,8) =[];   
y(:,8) =[];
%**********
%（1）先画出散点图，判断大致线性关系
figure(1)
plot(x,y,'+');
%（2）regress和rcoplt:数据格式化(样本对应行且第一列+1)
x1 =x';
y =y';
x=[ones(size(x1)),x1];
[b,bint,r,rint,stats] =regress(y,x);
b
bint
stats
figure(2)
rcoplot(r,rint);

1.图像分析

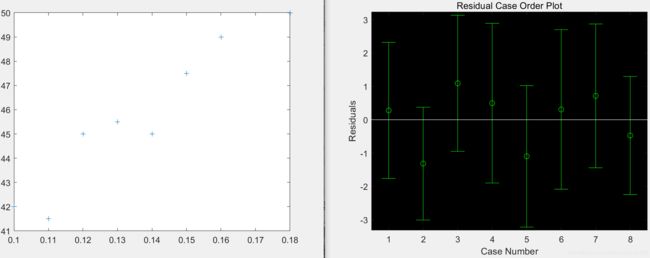
2.参数分析
b =30.7820 109.3985
bint =26.2805 35.2834 76.9014 141.8955
stats =0.9188 67.8534 0.0002 0.8797
3.结论
回归模型：y=30.782+109.3985*x1
其中（1）R^2>0.9,有很好的相关性

例2：多元线性回归

步骤：
①画出散点图，判断大致的线性/非线性关系
②regress和rcoplot回归与异常点剔除

1.图像分析


2.系数分析
b =66.5176 0.4139 -0.2698
bint =-32.5060 165.5411 -0.2018 1.0296 -0.4611 -0.0785
stats =0.6527（R^2） 6.5786 0.0247（概率P） 351.0445
3.结论
回归方程：y=66.517+0.4139x1-0.2698x2
其中（1）R^2<0.8，相关性不强 回归模型不好 （2）p=0.0247，当α=0.05时，p<α回归模型可用。因此尝试使用二次函数改进他。

4.2 多项式回归

例1：一元多项式回归

步骤：
①初始化数据(x,y一一对应，不需要样本放列)
②polyfit多项式回归
③polyconf计算函数值

clc,clear
x=17:2:29;
x=[x,x];
y=[20.48 25.13 26.15 30.0 26.1 20.3 19.35...
   24.35 28.11 26.3 31.4 26.92 25.7 21.3 ];
plot(x,y,'+');
%1.polyfit多项式回归
[p,s]=polyfit(x,y,2);   %p是系数，s用于计算函数值
p
%2.polyconf计算函数值
[y,delta]=polyconf(p,x,s);
y
polytool(x0,y0,2);

1.图像分析

2.系数分析
p =-0.2003 8.9782 -72.2150
即a2 = −0.2003，a1 = 8.9782 ，a0 = −72.2150。

或使用多项式回归工具箱polytool
polytool(x0,y0,2)

3.结论
回归方程：y=-0.2003x^2+8.9782x-72.215
函数值预测：[y,delta]=polyconf(p,x,s)。y为函数拟合值，delta为置信区间半径

例2：多元二项式回归

统计工具箱提供了统计工具箱提供了一个作多元二项式回归的命令rstool，它也产生一个交互式画面，并输出有关信息，用法是：
rstool(x,y,model,alpha)
x,y：分别为n × m 矩阵和n 维向量（n样本数为列）
alpha:显著性水平α （缺省时设定为0.05）
model:下列4个模型中选择1个



步骤：
①初始化数据（x=[x1,x2]，x1转置为样本数n为列）
②使用rstool工具箱
③传送数据与数据比较
一个菜单Export用以向Matlab工作区传送数据，包括beta(回归系数)，rmse（剩余标准差），residuals(残差)。

clc,clear
x1 =[120 140 190 130 155 175 125 145 180 150]';
x2 =[100 110 90 150 210 150 250 270 300 250]';
y =[102 100 120 77 46 93 26 69 65 85]';
x =[x1,x2];   %转置且连接成n*2的矩阵
rstool(x,y,'purequadratic')

1.图像分析
可以在交互式界面

reference

https://blog.csdn.net/pingmin2014/article/details/47298947 — 插值函数