【3D视觉原理】2-3D传感器原理
文章目录
- 内容概要
- 3D光学测量方法概述
-
- 被动测距
-
- 单目立体视觉(精度不高)
-
- 聚焦法
- 离焦法
- 双目立体视觉(精准)
- 多目立体视觉(更精准)
- 主动测距
-
- 结构光法
-
- 光点法
- 光条法
- 光面法
- 飞行时间法(ToF)
-
- 脉冲激光
- 连续激光
- 针孔相机模型
-
- 透镜模型
- 针孔模型
- 成像平面
- 传感器平面
- 传感器平面物理坐标&物体空间物理坐标
- 图像像素坐标(整数)转为传感器平面物理坐标
- 深度图数据转为点云数据
- 作业
- 双目3D视觉原理
-
- 如果只有RGB图,如何得到距离信息?
-
- 从视差得到3D坐标
-
- 视差匹配查找
- 视差匹配查找示例
-
- 要求
- 搜索时用到的图像特性。
- 搜索方案
- 匹配度如何计算?
- 视差图
-
- 为什么点云图中距离Z是离散的?
- OpenCV 视差计算(效果更好)
- 双目视觉计算作业
-
- 作业提示
- 双目视觉缺点 - 不适用于纹理单调(光滑)场景
- 双目视觉改进 - 投影特殊图案到光滑物体表面
- 结构光3D相机
-
- 点光源
- 线光源
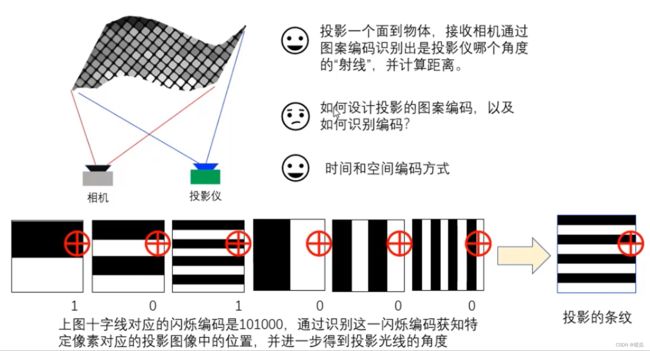
- 结构光编码
- TOF 3D成像原理
-
- 脉冲间隔测量法
-
- 直接飞行时间测量(DTOF, Direct ToF)
-
- 脉冲飞行时间(pToF,PluseToF)
- 幅度调制相位测量法
-
- 间接飞行时间测量(ITOF, Indirect ToF)
-
- 连续波飞行时间(cwToF,Continuous Wave ToF)
-
- 如何测量相位差?
- 模糊问题
-
- 双频去模糊
- 频率调制的相干测量法
-
- 基于条纹投影的3D成像
-
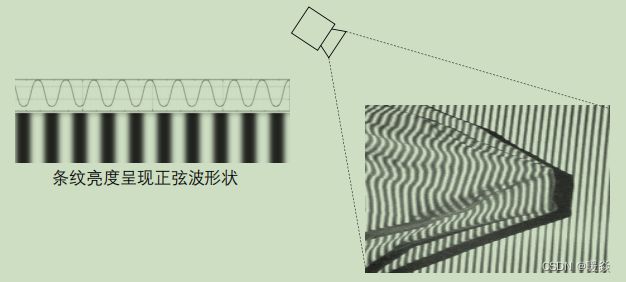
- 正弦亮度条纹
- ToF平面弯曲问题 - 像素到镜头距离->物体与像平面距离
- ToF Vs 结构光
- RGB-D 融合
-
- RGB-D 融合流程
- 深度相机三维点云坐标映射到RGB二维像素坐标
-
- Case1:旋转+平移
- Case2:只平移不旋转(深度相机与RGB相机平行)
- RGB-D 融合结果
- 镜头畸变矫正
-
- 镜头畸变矫正流程
- 像素坐标修正
- 基于Opencv镜头校准
-
-
- 平面弯曲问题(深度相机得到的深度d ≠ 物体到相机的距离Z)
-
- 软件安装
- TOF深度相机数据到点云转换
-
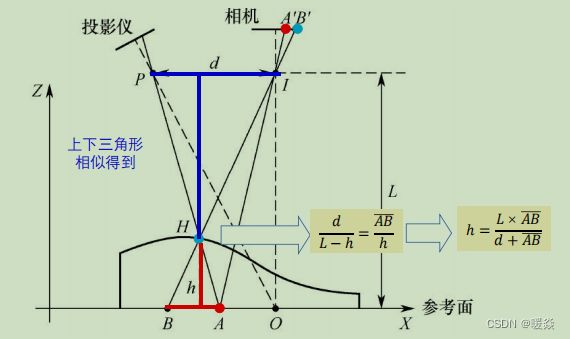
- 深度图-TOF 3D相机数据中距离Z的计算关系
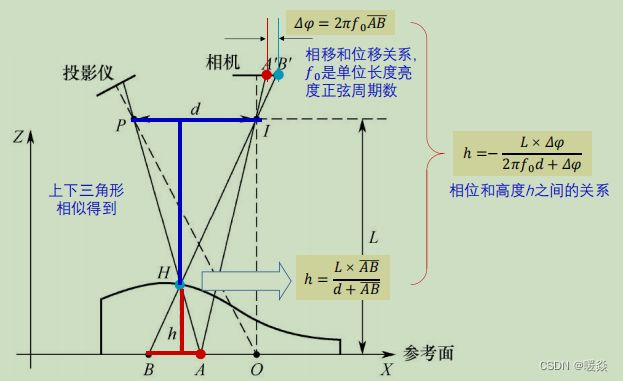
- 深度图-TOF 3D相机光源位置和物体距离的关系
- 深度图和点云的转换代码示例
- 点云重投影到深度图
-
- 遮挡 & 透射
- 作业
内容概要
3D光学测量方法概述
针孔相机模型.
双目3D视觉原理
结构光3D成像原理
TOF 3D成像原理
图像畸变与矫正
RGB-D融合概述
TOF深度相机数据到点云转换
深度图-TOF 3D相机数据中距离Z的计算关系
深度图-TOF 3D相机光源位置和物体距离的关系
点云重投影到深度图
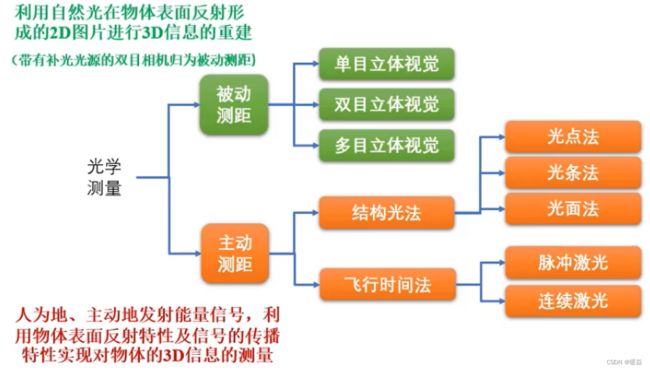
3D光学测量方法概述
被动测距
单目立体视觉(精度不高)
聚焦法
利用相机焦距可变的特性,变化焦距使被测量物体处于聚焦位置,然后利用成像公式计算出被测量物体距离相机的距离。
离焦法
不需要被测量物体处于焦距上,而是根据标定好的离焦模型计算物体与相机之间的距离。
双目立体视觉(精准)
在两个视点观察同一个场景,然后利用匹配算法计算两个图像像素的位置偏差进行3D测距。
多目立体视觉(更精准)
对双目立体视觉的扩展,多个视点观察同一个场景,进行多次匹配计算实现距离测量。
主动测距
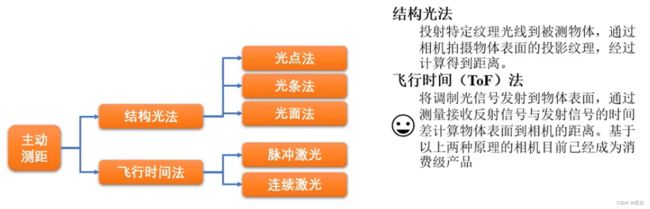
结构光法
光点法
光条法
光面法
飞行时间法(ToF)
脉冲激光
连续激光
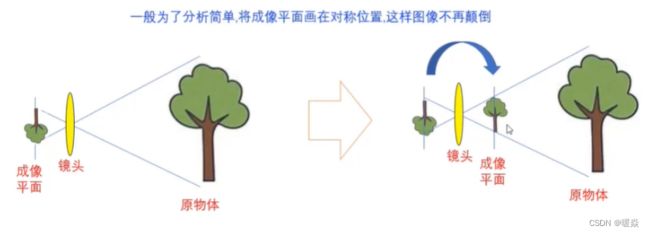
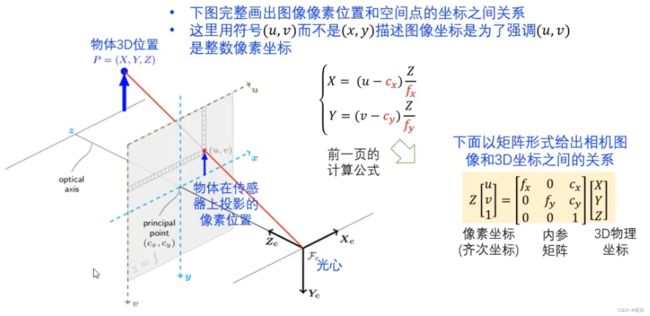
针孔相机模型
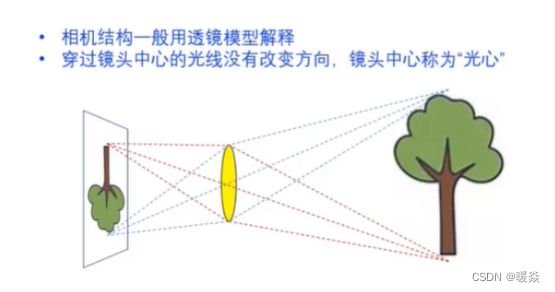
透镜模型
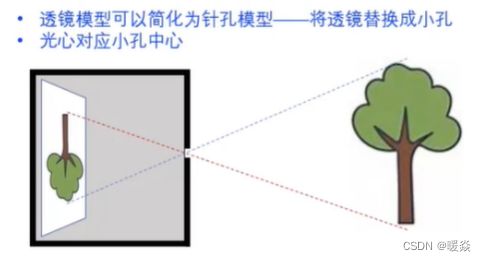
针孔模型
成像平面
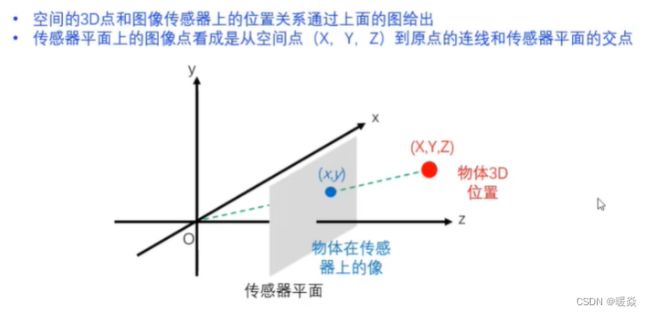
传感器平面
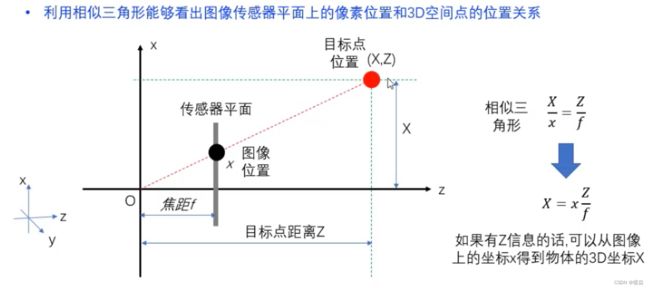
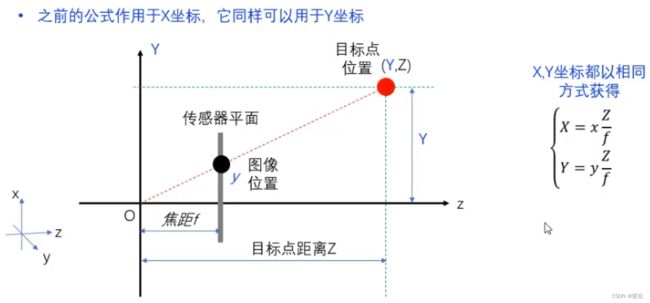
传感器平面物理坐标&物体空间物理坐标
图像像素坐标(整数)转为传感器平面物理坐标
图像像素坐标:图像的左上角为原点。
传感器平面物理坐标:坐标原点(光心)在传感器平面原点。
Z可以从深度图获取。
深度图数据转为点云数据
作业
双目3D视觉原理
前面可以看到,如果有每个像素点对应的物体的距离信息Z,则可以通过针孔相机模型,计算对应物体的三维坐标(X,Y,Z)。
作业中的距离信息Z是从深度图中获取的。
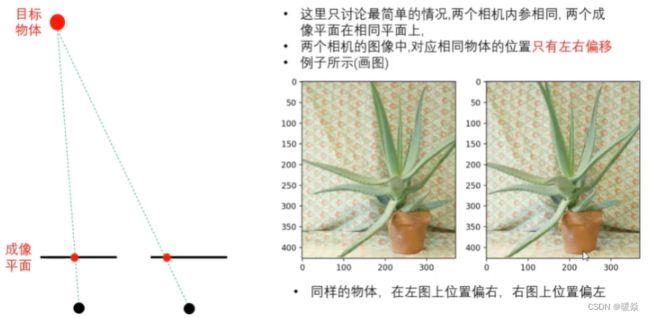
如果只有RGB图,如何得到距离信息?
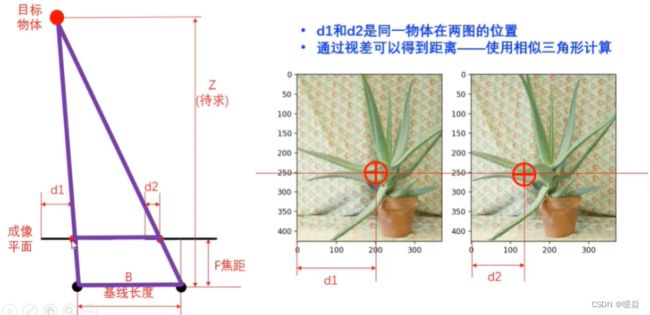
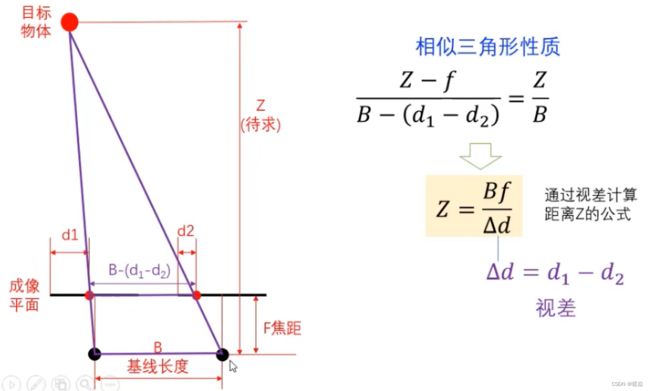
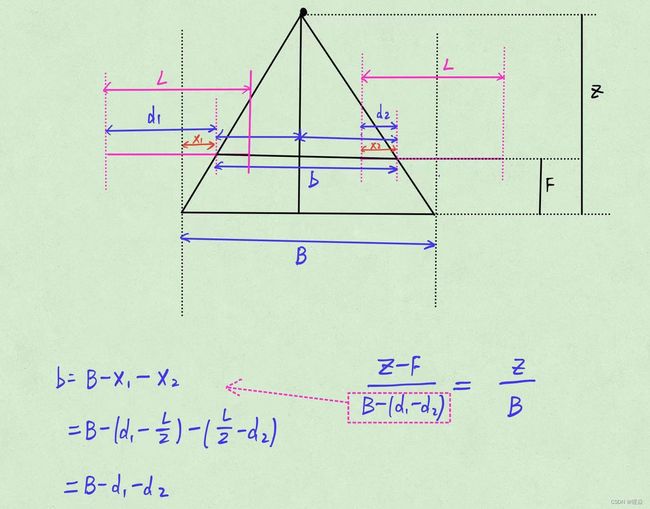
从视差得到3D坐标
Z Z Z与 Δ d \Delta d Δd成反比,这与人眼实际观察一样,物体离人眼越远,视差越小。
视差匹配查找
左图偏右,右图偏左。
视差匹配查找示例
要求
计算左图像(200,100)位置图像在右图中的位置。
搜索时用到的图像特性。
左右图像中同一物体对应的纵坐标相同,仅仅横坐标不同,并且右图像中物体"偏左"移动。
假设左右图像对应像素的水平偏移不超过30像素上述特性和假设帮助降低搜索的难度。
搜索方案
在右图中,从(200,100)位置开始搜索,依次检查右图位置(200,100)、(200-1.100)、 (200-2.100)…(200-30.100)的图像,看哪一个位置和左图(200,100)位置图像匹配度最高。
假设右图(200-d,100)位置匹配度最高,这就意味着在左图(200,100)处像素对应的物体在左右眼图像中的视差为d。
匹配度如何计算?
思想:差别通过像素的RGB3通道的色彩差的绝对值之和表示,该值越小,匹配程度越高。
为了提高匹配的准确性,我们需要匹配左图以(200,100)为中心的一个窗口内所有的像素,计算该窗口内每个像素和右图搜索位置对应窗口内所有像素的色彩差的绝对值的和(SAD) ,作为匹配度指标f(d),如右边公式所示
注意:公式中窗口尺寸参数W根据图像特性设置,比如这里的例子可以设W=2。
左图(x, y)位置像素和右图(x,y, d)位置像素的差异计算公式(SAD):
f ( x , y , d ) = ∑ d x W = − W ∑ d y W = − W ∣ I L ( x + d x , y + d y ) − I R ( x − d + d x , y + d y ) ∣ f(x,y,d)=\sum_{d_x}^{W}=-W\sum_{d_y}^{W}=-W|I_L(x+dx, y+dy)-I_R(x-d+dx, y+dy)| f(x,y,d)=∑dxW=−W∑dyW=−W∣IL(x+dx,y+dy)−IR(x−d+dx,y+dy)∣
其中
找到使得 f ( x , y , d ) f(x,y,d) f(x,y,d)最小的位置。
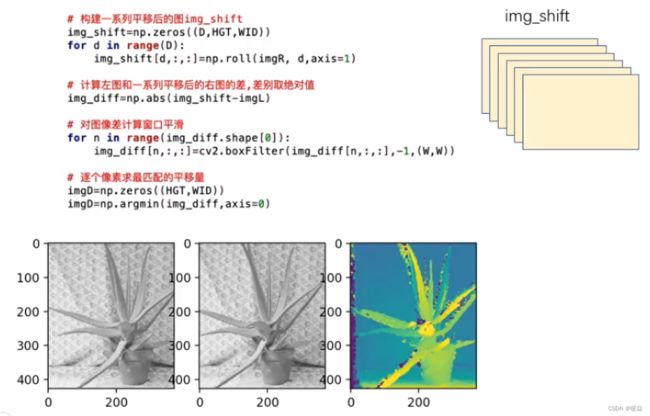
视差图
最右边图即为使用SAD算法得到的视差图,与深度图很像。
边缘匹配效果不好,因为对于物体左图看到的比右图看到的多,两张图片的视野范围不同,所以边缘匹配效果不好。
为什么点云图中距离Z是离散的?
两张图的分辨率比较小,因为计算视差时,视差都是整数,所以根据视差计算出的距离Z也是整数,所以距离Z是离散的。
OpenCV 视差计算(效果更好)
双目视觉计算作业
作业提示
双目视觉缺点 - 不适用于纹理单调(光滑)场景
适用于纹理丰富的场景,不适用于单调缺乏纹理的场景。
因为双目视觉根据视觉特征进行图像匹配,所以对于缺乏视觉特征的场景(如天空、白墙、沙漠等)会出现匹配困难甚至匹配失败,无法做像素级匹配。
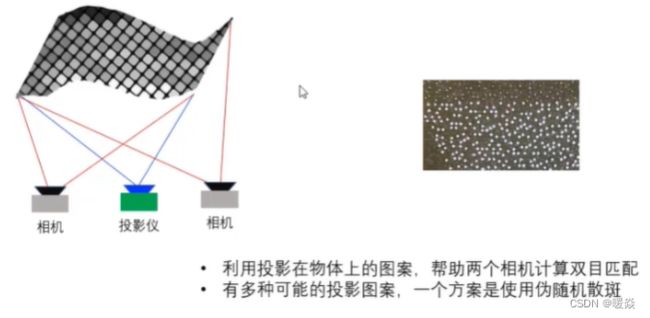
双目视觉改进 - 投影特殊图案到光滑物体表面
结构光3D相机
点光源
线光源
结构光编码
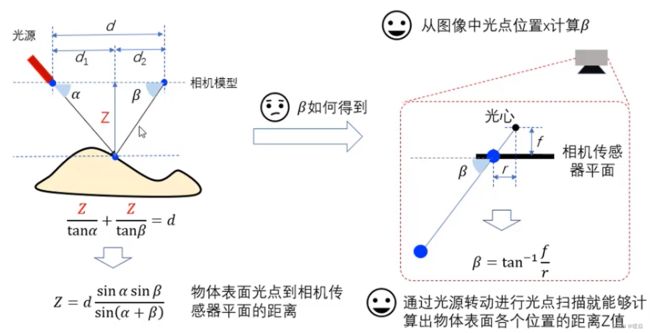
TOF 3D成像原理
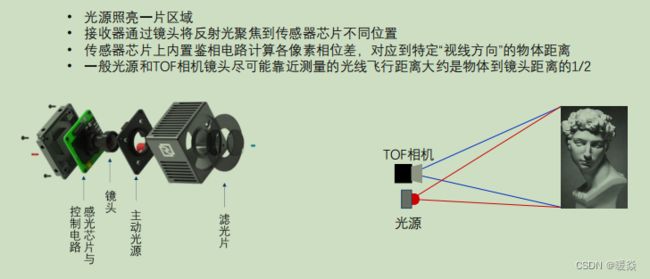
飞行时间法采用雷达测距的原理,通过测量光波从光源发出并经被测物体反射后回到传感器所需的时间,就可以获得距离信息。
注:一般光源和TOF相机镜头尽可能靠近,这种情况下,测量的光线飞行距离大约是物体到镜头距离的1/2,计算方便。
滤光片:一般ToF相机发射的是红外信号,滤光片是为了减少外部光源的干扰。
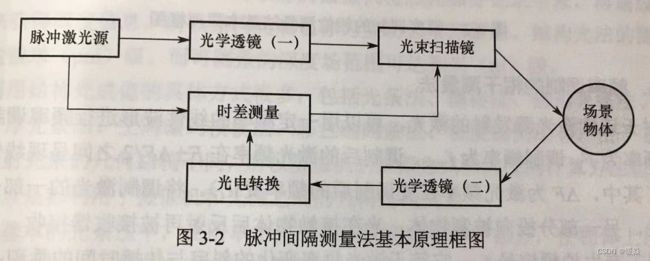
脉冲间隔测量法
时间差模块同时接收脉冲激光源直接发射的激光和经过光电转换的反射光,测量发射脉冲和接收脉冲的时间差。
直接飞行时间测量(DTOF, Direct ToF)
脉冲飞行时间(pToF,PluseToF)
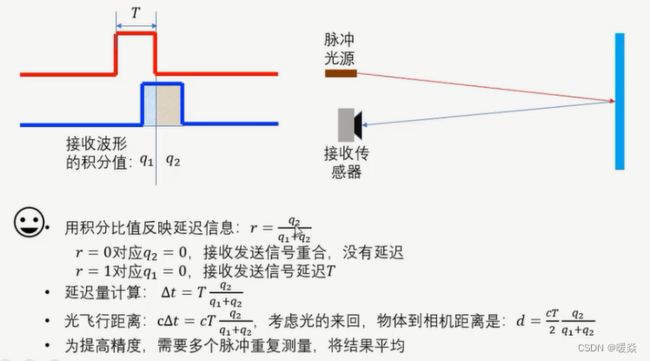
思想:测量脉冲时间差。
方法:利用方波脉冲间隔 或 超声波测量时间。
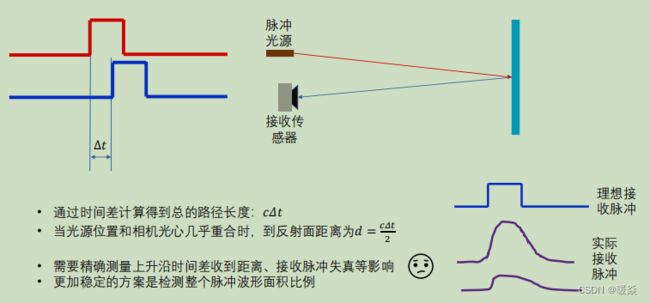
计算公式:时延(发送信号与接收信号时间差) Δ t \Delta t Δt,光速 c c c,被测距离 d d d,关系为 d = 1 2 c Δ t d=\frac {1}{2} c \Delta t d=21cΔt。
问题:需要精确测量上升沿时间差,实际使用时,因为接收距离、接收脉冲失真等影响,接收传感器的上升沿变形(并不是标准的方波),导致很难检测接收上升沿,所以时间差测量不准确,进而导致距离计算误差大。
改进1:将测量上升沿时间差改为测量积分值。使用简单的积分电路甚至一个电容就可以计算得到。
改进2:为了提高精度,经常使用多个脉冲重复测量,求平均得到测量结果。
幅度调制相位测量法
思想:测量相位差。
方法:利用幅度调制的连续波相位差测量时间。
间接飞行时间测量(ITOF, Indirect ToF)
思想:测量时间差。
方法:利用连续波相位差测量时间。
连续波飞行时间(cwToF,Continuous Wave ToF)
![]()
系数 a ∈ ( 0 , 1 ] a\in(0,1] a∈(0,1](已知); w w w调制信号频率(已知),一般是10m~100m;
ϕ \phi ϕ指飞行时间带来的相移量(待测量)。
F F F 光调制信号的频率。
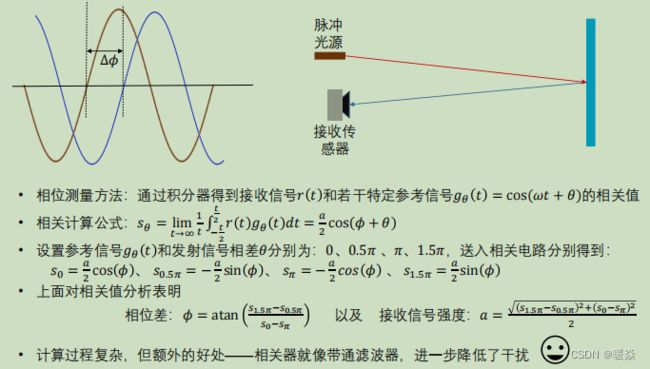
如何测量相位差?
θ \theta θ:参考信号与发送信号固定的相移。(已知,且有多个参考信号)
ϕ \phi ϕ:接收信号的相位差。(未知)
a a a:接收信号的强度。(未知)
脉冲时间差的方法只需要计算积分即可,相位差的方法需要计算4个相关值才能得到结果,但是也因为这个原因相位差方法得到的结果更好。
相关器相当于一个带通滤波器,滤波器的中心频率就是光信号的调制频率,在一定程度上可以过滤掉干扰信号,可以提高接收信号的质量。
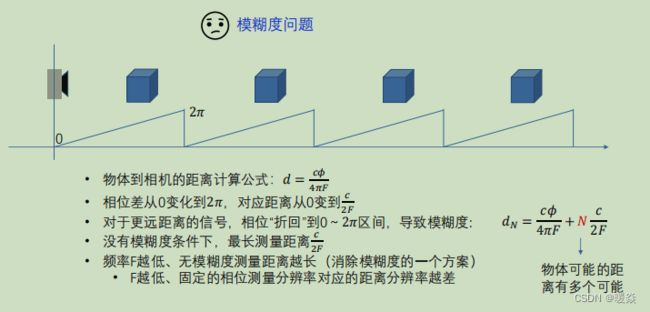
模糊问题
无论是时间差还是相位差,在实际使用时,都有模糊问题。以下以计算相位差获得距离方法为例说明模糊问题。
模糊问题:相位差超过一个周期。但是通过以上介绍的方法和公式只能计算一个周期内的相位差。一般物体离相机的距离比较远时会出现模糊问题。
如果多个物体距离相机的距离相差整数倍的 c 2 F \frac {c}{2F} 2Fc的距离,那么通过公式计算出的相位差是一样的,这其实是错误的计算结果,也就是,不能只通过公式计算唯一确定物体离相机的距离。
一种方式是降低调制频率F,当F很小时,离相机近的物体反射的信号正常,离相机远的物体反射的信号会很弱,进而区别出距离相机不同距离的物体。但是这种方式的缺点是频率F越低,相位测量的分辨率也低,导致距离测量准确度不高,想提高准确率,就得增大F,又导致模糊问题严重,所以这种方式不可行。
双频去模糊
两种频率分别测量出不同可能距离分别为 d 1 + N D 1 d_1+ND_1 d1+ND1、 d 2 + N D 2 d_2+ND_2 d2+ND2,两种可能距离中一定能匹配到相同位置(可能有多个),这个位置就是物体的真实距离。
但即使是双拼测试,也会匹配出多个相同位置,只是相较单频率测试多个相同位置间的距离会更大,更容易通过信号的强弱判断出物体的远近,得到更精确的结果,一定程度上解决模糊度问题。
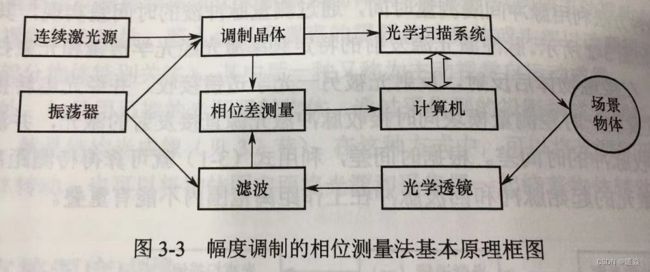
频率调制的相干测量法
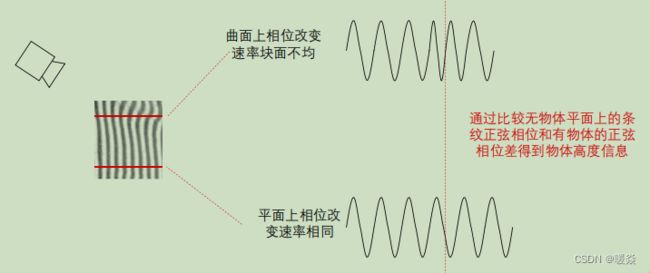
思想:测量高度差。
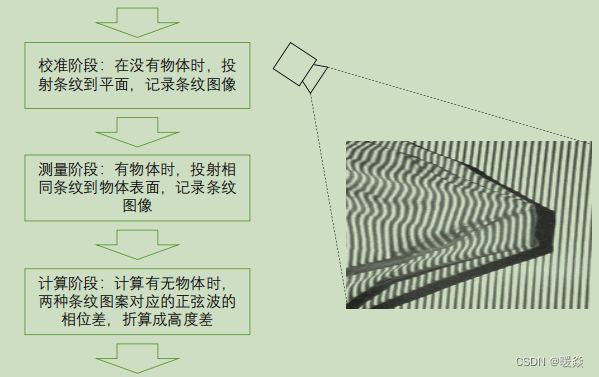
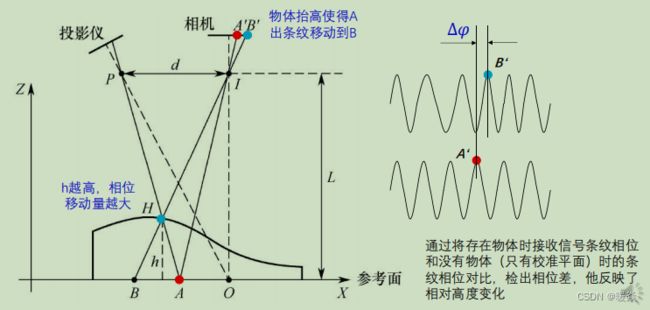
实现:利用不含物体(校准平面)时的条纹相位和含物体时接收信号条纹相位对比得出相位差,相位差反映了相对高度变化。
基于条纹投影的3D成像
正弦亮度条纹
ToF平面弯曲问题 - 像素到镜头距离->物体与像平面距离
ToF Vs 结构光
RGB-D 融合
方法:RGB+Depth,将RGB图色彩映射到深度图,为从深度相机得到的每个点云“染色”。
目的:使得后续应用计算过程中可以使用RGB算法和RGB现有的一些成果。
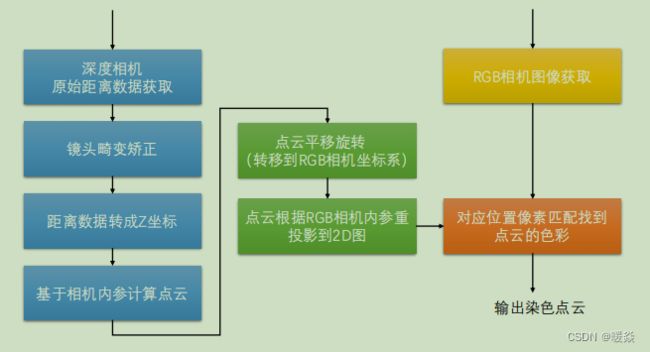
RGB-D 融合流程
点云平移旋转是为了将深度相机看到的图像旋转为RGB相机看到的图像。
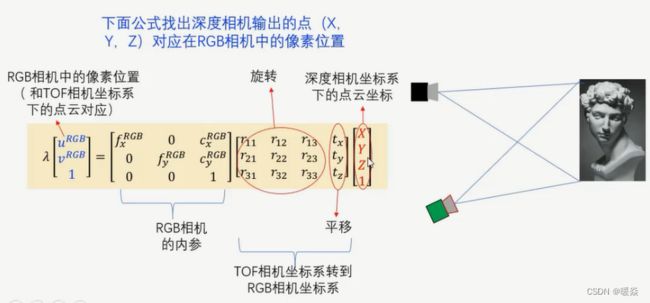
深度相机三维点云坐标映射到RGB二维像素坐标
Case1:旋转+平移
通常将上述公式计算出的三维向量中的Z方向的值 λ \lambda λ作为归一化值,则X方向和Y方向归一化后得到 ( u R G B , v R G B ) (u^{RGB},v^{RGB}) (uRGB,vRGB)即为深度相机三维点云坐标映射到RGB相机的像素坐标。
Case2:只平移不旋转(深度相机与RGB相机平行)
![]()
RGB-D 融合结果
镜头畸变矫正
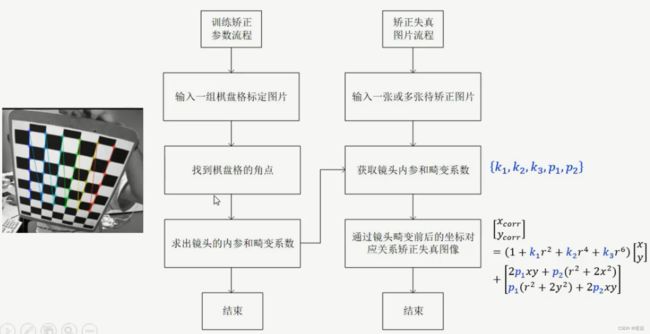
镜头畸变矫正流程
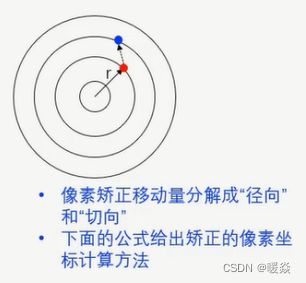
像素坐标修正
基于Opencv镜头校准
角点粗检测:grap表示原始图片,(7,6)表示7行6列角点。
角点精检测:检测结果中的像素坐标不是整数级而是亚像素级的坐标,比粗检测的结果更准确。
计算矫正模型参数:结果总mtx为内参矩阵,dist为失真参数向量。
图像矫正:img原图。
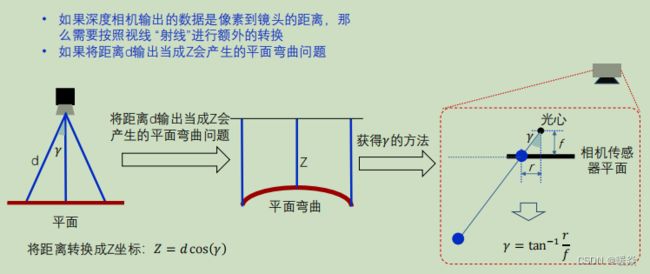
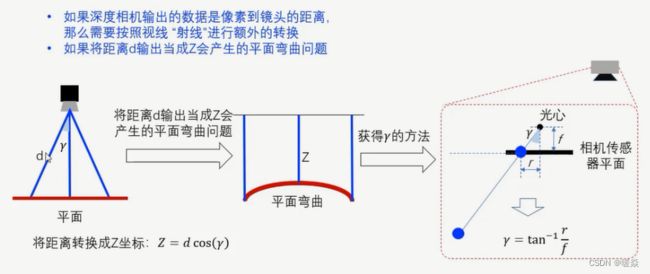
平面弯曲问题(深度相机得到的深度d ≠ 物体到相机的距离Z)
深度相机得到的深度d:像素到镜头的距离(视线“射线”)。
物体到相机的距离z:物体垂直于相机平面的距离。
d修正为z: Z = d c o s ( γ ) , γ = t a n − 1 r f Z=dcos(\gamma), \gamma=tan^{-1} \frac {r}{f} Z=dcos(γ),γ=tan−1fr。
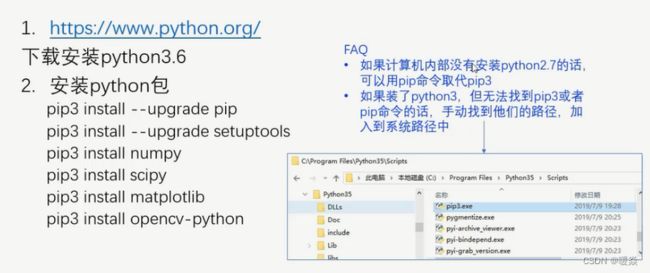
软件安装
TOF深度相机数据到点云转换
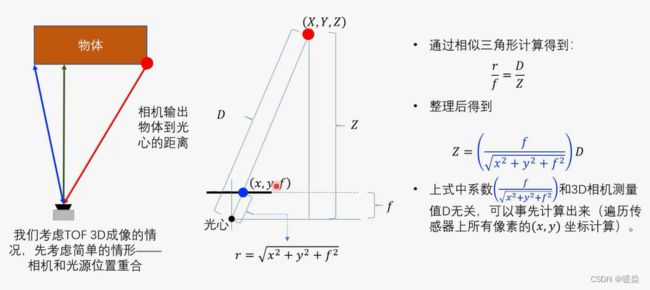
深度图-TOF 3D相机数据中距离Z的计算关系
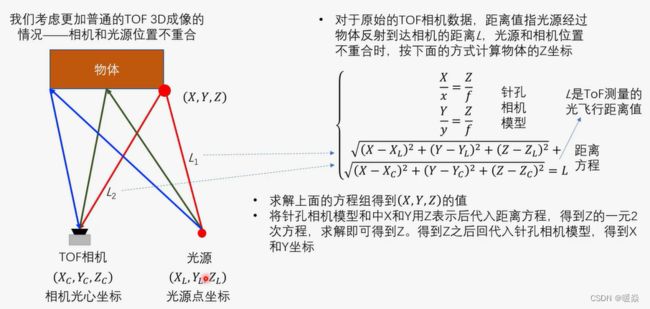
深度图-TOF 3D相机光源位置和物体距离的关系
深度图和点云的转换代码示例
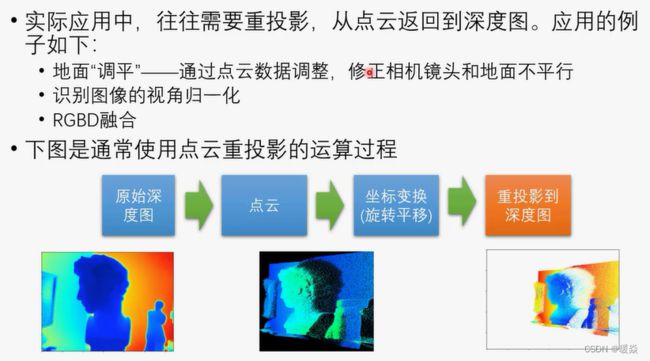
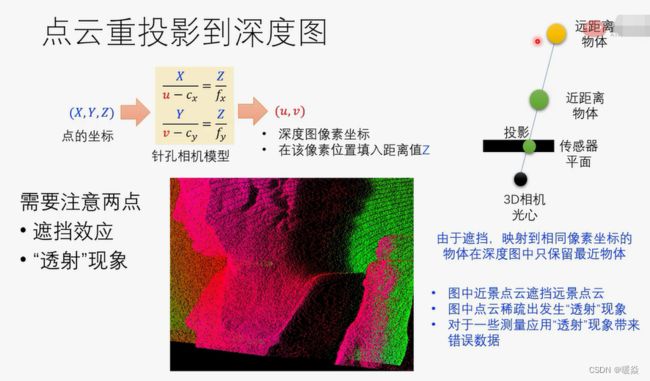
点云重投影到深度图
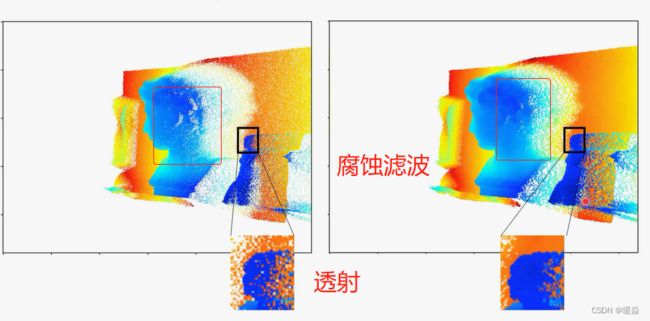
遮挡 & 透射
腐蚀滤波会使得整张图偏近。